Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (22 of 92) Prob. of Finding Particle 2

Michel van Biezen
20 Feb 201706:07
EducationalLearning
32 Likes 10 Comments

TLDRIn the video, the presenter explores the probability of finding a particle within a specific interval in a one-dimensional infinite well for the second energy level (n=2). By calculating and normalizing the probability function, the video demonstrates that the particle has a 25% chance of being found between 0 and L/4, L/4 to L/2, L/2 to 3L/4, and the last L/4. This illustrates the symmetry and effectiveness of the probability function in determining a particle's location within the well.

Takeaways
  • ๐Ÿ“Œ The video discusses the probability of finding a particle within a specific interval in a one-dimensional well.
  • ๐Ÿ”ข In the previous video, the probability of finding a particle between x=0 and x=L/4 was found to be approximately 9%.
  • ๐Ÿฅผ The current analysis focuses on the energy level n=2 and examines the probability function for this level.
  • ๐Ÿ“ˆ The probability function for n=2 is calculated and normalized to find the probability across the entire curve.
  • ๐Ÿค” The integral of the wave function squared is used to calculate the probability, as there is no imaginary part involved.
  • ๐Ÿ“š The trigonometric identity for sine squared is applied to separate the integral into two parts for calculation.
  • ๐Ÿงฎ The integrals are evaluated, and the proper differential (dX) is determined to be L/(2nPI).
  • ๐ŸŒ€ The symmetry of the wave function is highlighted, which affects the probability distribution.
  • ๐ŸŽฏ The final probability of finding the particle between 0 and L/4 is calculated to be 1/4 or 25%.
  • ๐Ÿ“Š The probability function effectively demonstrates the likelihood of a particle's position within the one-dimensional well.
  • ๐Ÿ”š The process concludes with the confirmation that the expected probability matches the calculated result.
Q & A

  • What was the probability of finding a particle between x=0 and x=L/4 in the previous video?

    -The probability of finding a particle between x=0 and x=L/4 in the previous video was about 9%.

  • What is the significance of the probability function in the context of a one-dimensional well?

    -The probability function represents the likelihood of finding a particle within a certain region of the one-dimensional well. It is derived from the wave function of the particle.

  • How does the wave function change for the energy level n=2 compared to n=1?

    -The wave function for the energy level n=2 looks different from n=1, which in turn affects the shape of the probability function and the distribution of probabilities across different regions of the well.

  • What is the expected probability of finding the particle between 0 and L/4 for the n=2 energy level?

    -The expected probability of finding the particle between 0 and L/4 for the n=2 energy level is about 25%.

  • How is the probability calculated for a specific interval in the one-dimensional well?

    -The probability is calculated by integrating the square of the wave function over the interval of interest. This involves integrating the function without an imaginary part, which simplifies the process.

  • What trigonometric identity is used to simplify the probability function for n=2?

    -The trigonometric identity used to simplify the probability function for n=2 is the sine square identity, which is 1/2 * (1 - cos(2ฮธ)), where ฮธ is the angle in question.

  • How are the integrals separated for the probability calculation of n=2?

    -The integrals are separated by using the trigonometric identity and evaluating them as two distinct integrals: one for the sine function and one for the cosine function, each integrated over the interval from 0 to L/4.

  • What is the role of the proper differential in the integral calculation?

    -The proper differential, which is L/(2ฯ€) in this case, is used to adjust the differential DX to account for the angular frequency (2ฯ€/L) in the integral, ensuring the correct calculation of the area under the curve.

  • How does the symmetry of the wave function affect the probability distribution?

    -The symmetry of the wave function results in equal probabilities for the particle to be found in each quarter of the one-dimensional well, with a 25% chance in each interval from 0 to L/4, from L/4 to L/2, from L/2 to 3L/4, and from 3L/4 to L.

  • What is the final result of the probability calculation for the particle between 0 and L/4 in the n=2 energy level?

    -The final result of the probability calculation for the particle between 0 and L/4 in the n=2 energy level is 1/4, which is equivalent to 0.25 or 25%.

  • How does the probability function demonstrate its effectiveness in the one-dimensional well model?

    -The probability function effectively predicts the distribution of the particle's likelihood across the one-dimensional well, showing clear patterns of probability that align with the expected results based on the particle's energy level and the properties of the well.

Outlines
00:00
๐ŸŒŸ Quantum Mechanics: Probability in a One-Dimensional Well

This paragraph delves into the quantum mechanics concept of finding the probability of a particle's location within a one-dimensional well. It explains how the probability of discovering a particle between x=0 and x=L/4 (the first 1/4 of the well) is approximately 9%. The discussion then shifts to calculating the probability for the energy level n=2, highlighting changes in the wave function and its probability distribution. The process involves integrating the wave function squared over the interval and normalizing the result, leading to a predicted 25% probability. The calculation is carried out using trigonometric identities and separation of variables, ultimately confirming the expected result.

05:01
๐Ÿ“Š Probability Distribution Analysis for n=2 States

The second paragraph continues the analysis of quantum states, focusing on the probability distribution for n=2 in a one-dimensional well. It emphasizes the symmetry of the particle's probability distribution, revealing that there is a 25% chance of finding the particle in each quarter-section of the well. The explanation includes the mathematical derivation of the probability for the first quarter (0 to L/4) and shows how the remaining quarters follow a similar pattern. The conclusion is that the probability function effectively predicts the likelihood of a particle's position as it moves within the confines of the well, demonstrating the practical application of quantum mechanics in determining particle behavior.

Mindmap
Keywords
๐Ÿ’กElectron Line
The term 'Electron Line' likely refers to the context of the video being about electron behavior in a one-dimensional well, specifically addressing the probability of finding an electron within certain regions of the well. It is a conceptual framework used in quantum mechanics to describe the movement and location probabilities of electrons.
๐Ÿ’กProbability
In the context of the video, 'probability' refers to the likelihood of finding a particle, in this case, an electron, within a specified range of a one-dimensional well. It is a fundamental concept in quantum mechanics, indicating the chances of a specific outcome or event, such as the presence of an electron in a certain region.
๐Ÿ’กOne-Dimensional Well
A 'one-dimensional well' is a theoretical model in quantum mechanics that represents a potential well or barrier in one dimension, which confines a particle, like an electron, to move only back and forth along a line. This model is used to study the quantization of energy levels and the behavior of particles under confinement.
๐Ÿ’กWave Function
The 'wave function' is a mathematical description in quantum mechanics that provides information about the quantum state of a system, such as the probability amplitude of a particle's location. It is a fundamental concept used to calculate the probabilities of various outcomes in quantum systems.
๐Ÿ’กNormalization
Normalization in the context of quantum mechanics refers to the process of adjusting the wave function so that the total probability of finding the particle anywhere in the entire space sums up to 1. This ensures that the probabilities calculated are consistent with the interpretation of the wave function.
๐Ÿ’กTrigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the context of the video, trigonometry is used to separate and simplify the integrals involved in calculating the probability.
๐Ÿ’กIntegral
In mathematics, an 'integral' represents the accumulation of a quantity, such as area under a curve, which is a fundamental concept in calculus. In the video, integration is used to calculate the probability of finding a particle within a certain range by integrating the wave function squared over that range.
๐Ÿ’กSine and Cosine
Sine and cosine are trigonometric functions that relate the angles and sides of a right triangle. They are used in the video to describe the shape of the wave function and to perform the necessary calculations for the probability integrals.
๐Ÿ’กEnergy Level
In quantum mechanics, 'energy levels' refer to the quantized, discrete levels of energy that a particle can possess within a system, such as an electron within an atomic orbital. The energy levels determine the possible states of the particle and are key to understanding quantum behavior.
๐Ÿ’กQuantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. It provides a framework for understanding the probabilistic nature of particles and their interactions, as well as the quantization of energy and other physical properties.
๐Ÿ’กSymmetry
In the context of the video, 'symmetry' refers to the balanced distribution of the probability across the one-dimensional well. The particle has an equal chance of being found at symmetrical intervals within the well, which is a result of the wave function's properties and the system's symmetry.
Highlights

The video discusses the probability of finding a particle in a specific location within a one-dimensional well.

In the previous video, the probability of finding a particle between x=0 and x=L/4 was calculated to be about 9%.

The current video focuses on calculating the probability for the energy level n=2.

The wave function for n=2 looks different, affecting the probability function.

The area under the curve of the probability function represents the probability of finding the particle in a given interval.

The calculated probability for n=2 is expected to be about 25%.

The probability is calculated by integrating over the wave function squared.

The integral is separated into two parts using trigonometric identities.

The proper differential is determined for the integral.

The integrals are evaluated, resulting in the probability for the particle being between 0 and L/4.

The probability calculation confirms the expected result of 1/4 or 0.25.

The symmetry of the particle's wave function affects the distribution of probability across the one-dimensional well.

The probability function effectively determines the likelihood of finding a particle in a specific interval.

The video demonstrates the practical application of quantum mechanics in understanding particle behavior in a one-dimensional infinite well.

The method used can be generalized to calculate probabilities for different energy levels and wave functions.

The video provides a clear example of how mathematical models can predict physical phenomena in quantum mechanics.

Transcripts

Browse More Related Video

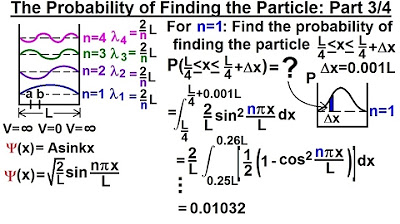
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (23 of 92) Prob. of Finding Particle 3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (27 of 92) Expectation Value=? 1-D Box n=1

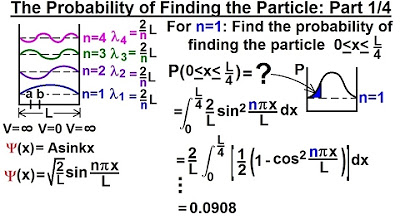
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (21 of 72) Prob. of Finding Particle 1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (34 of 92) Finite Potential Well Part 3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (25 of 92) Prob. of a Particle 1-D Box n=1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (20 of 92) Particle in 1-D Box: Example 2/2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsProbability CalculationOne-Dimensional WellParticle PhysicsWave FunctionsEnergy LevelsSine FunctionsIntegrationTrigonometryPhysics Education