Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (23 of 92) Prob. of Finding Particle 3

Michel van Biezen
24 Feb 201708:38
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the calculation of the probability of finding a particle in a specific location within a potential well. It explains the process of defining the region of interest and using the probability density function to find the likelihood at the first energy level. The script details the mathematical steps, including the use of trigonometric identities and integration, to arrive at the probability for a small region between L/4 and L/4 + Ξ”X. The result provides an understanding of the particle's presence in that area and hints at a method for approximating the result more efficiently.

Takeaways
  • 🌟 The topic is finding the probability of a particle being in a specific location, using the electron line model.
  • πŸ“ The region of interest is between x = L/4 and x = L/4 + Ξ”X, with Ξ”X being a very small distance (0.01L).
  • 🧬 The probability is calculated using the probability density function, which is the square of the wave function at each point.
  • 🌊 The wave function for the first energy level (N=1) is considered, which is real and does not require complex conjugate multiplication.
  • πŸ“ˆ The calculation involves integrating the sine squared of an angle, using the trigonometric identity (1 - cos(2ΞΈ))/2.
  • πŸ”’ The integral is computed over the specified limits (0.25L to 0.26L), with the proper differential (2Ο€/L * dx).
  • πŸ“Œ The result simplifies to a difference in sines of the upper and lower limits, divided by L and 2Ο€.
  • 🎯 As Ξ”X approaches zero, the probability of finding the particle at the exact location L/4 approaches 0.1.
  • πŸ” The method can be used to find the probability of finding the particle at any point along the path, offering a 1% chance at any given point.
  • πŸš€ The approach demonstrates how to calculate probabilities for particles in quantum mechanics, particularly in a one-dimensional infinite potential well.
Q & A

  • What is the main objective of the discussion in the transcript?

    -The main objective is to find the probability of finding a particle in a particular location, specifically between x equals L/4 and a small distance farther (Delta X).

  • How is Delta X defined in the context of the transcript?

    -Delta X is defined as a very small distance, specifically 0.01L, representing the range in which the probability of finding the particle is being calculated.

  • What is the significance of the first energy level (N equals 1) in this discussion?

    -At the first energy level (N equals 1), the probability density function is used to find the particle at any point between 0 and L, which is crucial for calculating the probability in the specified region.

  • How is the probability calculated for the particle being between L/4 and L/4 + Delta X?

    -The probability is calculated by integrating the square of the wave function (since it's real and doesn't require complex conjugation) over the interval from L/4 to L/4 + Delta X.

  • What trigonometric identity is used in the calculation?

    -The trigonometric identity used is 1/2 * (1 - cos(2 * angle)), where the angle is 2 * n * PI * x / L.

  • How does the integral change when Delta X becomes very small?

    -As Delta X approaches zero, the second part of the interval becomes infinitely small, and the probability of finding the particle at exactly that location (L/4) approaches 0.1.

  • What is the final probability calculated for the particle being in the region from x equals L/4 to x equals L/4 plus Delta X?

    -The final probability calculated is approximately 0.0103L, or a 1% chance of finding the particle in that small region.

  • Why is the wave function used in the calculation without its complex conjugate?

    -The wave function is used without its complex conjugate because it does not have an imaginary part at the first energy level (N equals 1).

  • What does the probability density function represent in this context?

    -The probability density function represents the probability of finding the particle at any point between 0 and L at the first energy level.

  • How does the probability change as we make Delta X smaller?

    -As Delta X becomes smaller, the probability of finding the particle at a specific location (L/4) increases, approaching 0.1 or 10% as Delta X goes to zero.

Outlines
00:00
πŸ” Calculating Particle Probability in a Defined Region

This paragraph explains the process of determining the probability of finding a particle within a specific region. It introduces the concept of defining a region between two points, x equals L/4 and x equals L/4 + Ξ”X, where Ξ”X is a very small distance (0.01L). The discussion revolves around the probability density function and the calculation of probability by integrating the wave function's square over the defined region. The integral is broken down into two parts, and the trigonometric identity for sine squared is applied. The calculation involves finding the difference in sine values at the upper and lower limits of the integral, which simplifies to a result that represents the probability of finding the particle in the given region.

05:02
πŸ“‰ Probability as Ξ”X Approaches Zero and the 1% Chance

The second paragraph delves into the implications of making Ξ”X, the interval for finding the particle, increasingly smaller. It explains that as Ξ”X approaches zero, the probability of finding the particle at an exact location (L/4) converges to a specific value, which is 0.1 in this case. The paragraph emphasizes the concept that the probability of finding the particle anywhere along the path within the small region is about 1%, and this probability can be calculated for any specific point along the particle's path. The explanation concludes with a discussion on the mathematical approach to finding the particle's probability at any given point in the region.

Mindmap
Keywords
πŸ’‘probability
In the context of the video, 'probability' refers to the likelihood of finding a particle in a specific location within a defined region. It is a fundamental concept in quantum mechanics, used to describe the chance of a particle's presence at a particular point. The video discusses calculating this probability by integrating the square of the wave function over a certain interval, which in this case is between L/4 and L/4 + Delta X.
πŸ’‘particle
A 'particle' in this video script refers to a subatomic entity, such as an electron, that is being studied within a quantum mechanical system. The particle's behavior is described by its wave function, and the probability of finding it in a specific location is the main focus of the video. The particle is associated with a probability density function, which is used to determine the likelihood of it being in a certain region.
πŸ’‘wave function
The 'wave function' is a mathematical description in quantum mechanics that provides information about a particle's state. It is used to calculate the probability of finding a particle at a certain location. In the video, the wave function is used to determine the probability density function, which is then squared to find the probability of the particle's presence in a given region.
πŸ’‘energy level
An 'energy level' in quantum mechanics refers to the quantized states of energy that a particle can have within a system. The video is specifically discussing the first energy level (N=1), which is the simplest state of the particle within the potential well. The energy levels determine the possible values of energy the particle can possess and are crucial in calculating the wave function and probability distributions.
πŸ’‘potential well
A 'potential well' is a region in space where the potential energy of a particle is lower than its surroundings, effectively trapping the particle within that region. In the context of the video, the particle is confined within a potential well, and the probability of finding it is being calculated within this confined space.
πŸ’‘trigonometric identity
A 'trigonometric identity' is a relationship between different trigonometric functions that is always true. In the video, the identity used is for the sine squared of an angle, which is expressed as 1/2(1 - cos(2ΞΈ)). This identity is crucial for simplifying the mathematical expression used to calculate the probability of finding the particle in the specified region.
πŸ’‘integration
Integration is a mathematical process that finds the area under a curve defined by a function over a certain interval. In quantum mechanics, integration is used to calculate probabilities by integrating the square of the wave function over the space in which the particle could exist. The video describes the process of integration to find the probability of the particle's location.
πŸ’‘differential
A 'differential' is a mathematical term used to describe a small change in a variable. In the context of the video, the differential (dX) represents an infinitesimally small change in the position of the particle, which is necessary for performing the integration to find the probability of the particle's location.
πŸ’‘limits of integration
The 'limits of integration' are the boundaries that define the interval over which an integral is calculated. In the video, these limits are the specific values between which the probability of finding the particle is being determined. The limits are crucial in calculating the probability as they define the region of interest.
πŸ’‘quantum tunneling
Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier that it classically shouldn't be able to overcome. Although not explicitly mentioned in the video script, the concept of finding the probability of a particle's presence in a certain region is related to understanding the behavior of particles at the quantum level, which includes phenomena like quantum tunneling.
πŸ’‘radians
Radians are a unit of measure used to describe angles in the context of trigonometry and calculus. In the video, the term 'radians' is relevant when calculating the sine of an angle, specifically when evaluating the trigonometric functions involved in the integration process to find the probability of the particle's location.
Highlights

The main objective is to find the probability of a particle being in a specific location.

The region of interest is defined between x equals L/4 and a small distance farther (Delta X = 0.01L).

The probability is calculated for the first energy level (N=1) of the particle in a one-dimensional box.

The probability density function is used, which is the product of the wave function since it's real-valued.

The integral involves the sine squared of an angle, which can be simplified using a trigonometric identity.

The limits of integration are 0.25L and 0.26L, representing the region of interest.

The integral is separated into two parts for easier calculation.

The proper differential is used in the integral, which involves multiplying by 2Ο€/L.

The integral of the cosine function results in the sine function, which simplifies the expression.

The probability is found by evaluating the sine functions at the upper and lower limits of integration.

The final probability expression is simplified by canceling out L and combining terms.

The probability of finding the particle in the small region is approximately 0.0103L.

As Delta X approaches zero, the probability of finding the particle at an exact location becomes a definite value.

The process can be used to find the probability of finding the particle at any point along the path.

The method provides a way to calculate the probability distribution of a particle in a quantum system.

The approach demonstrates the application of wave functions and quantum mechanics principles in determining particle location probabilities.

The explanation includes a step-by-step breakdown of the mathematical process, making it accessible for understanding.

Transcripts

Browse More Related Video

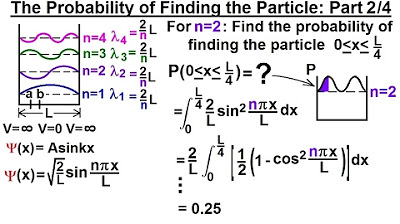
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (22 of 92) Prob. of Finding Particle 2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (25 of 92) Prob. of a Particle 1-D Box n=1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (10 of 92) What is Normalization? Ex. 1

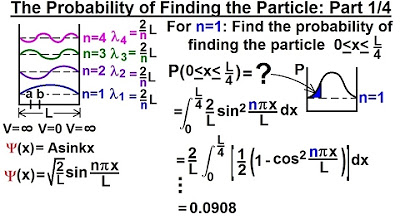
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (21 of 72) Prob. of Finding Particle 1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (27 of 92) Expectation Value=? 1-D Box n=1

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (24 of 92) Prob. of Finding Particle 4

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsProbability CalculationFirst Energy LevelParticle LocationElectron BehaviorTrigonometric IdentitiesWave FunctionIntegrationPhysics EducationScientific AnalysisMathematical Approach