Is Symmetry Fundamental to Reality? Gauge Theory has an Answer
TLDRThe video script explores the concept of symmetry in physics, highlighting its fundamental role in understanding the universe. It explains how symmetry leads to conserved quantities, as exemplified by Noether's theorem, and connects this to fundamental forces like electromagnetism. The script uses the equilateral triangle and circle as analogies to illustrate symmetry and group theory, leading to the revelation that the standard model's fundamental forces arise from specific symmetry groups. The lecture encourages further exploration of symmetry's power and beauty in physics through a recommended course on Wondrium.
Takeaways
- 🔍 Physicists use symmetry as a fundamental concept to understand the universe, akin to detectives searching for clues.
- 🌟 Symmetry in physics often leads to conserved quantities, such as the law of conservation of energy and momentum.
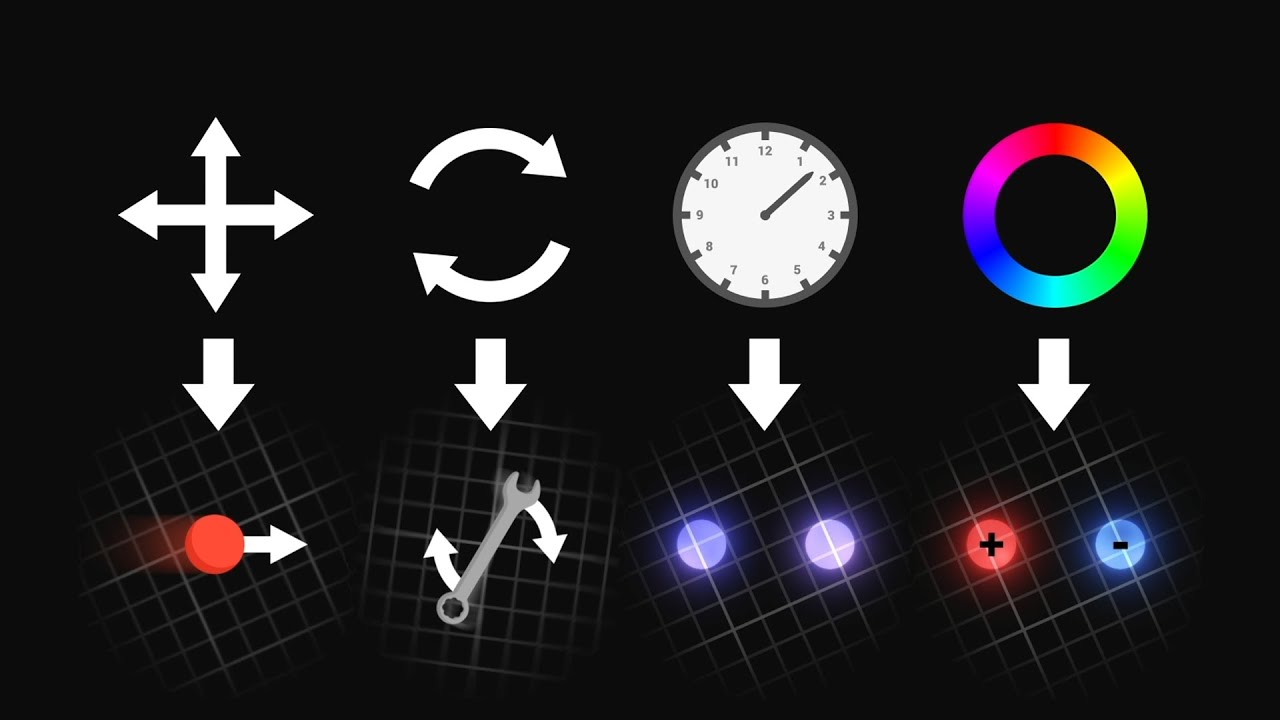
- 📐 The concept of symmetry involves actions that do not visibly change an object, like reflections and rotations of geometrical shapes.
- 🤔 Group theory is the mathematical framework behind the symmetries, describing the operations that can be performed on an object while preserving its symmetry.
- 🔄 The dihedral group is an example of a group theory used to describe the symmetries of shapes like triangles and squares.
- 📈 Noether's theorem connects symmetries with conservation laws, stating that every symmetry corresponds to a conserved quantity.
- 🔄 The U(1) group, associated with circles, is an example of a symmetry group that leads to the conservation of electric charge and is fundamental to the electromagnetic force.
- 🤹 The standard model of particle physics is built upon respecting certain symmetries, which correspond to the fundamental forces of the universe.
- 🌐 The SU(2) and SU(3) groups are more complex symmetry groups that correspond to the weak force and strong force, respectively.
- 🎯 Each generator in a gauge group corresponds to a force-mediating particle, like the photon for the electromagnetic force.
- 🚀 The search for understanding symmetry and its role in physics is ongoing, with resources like Wondrium offering in-depth educational content on the subject.
Q & A
What is the fundamental concept that physicists often associate with the core of physics theories?
-The fundamental concept that physicists often associate with the core of physics theories is symmetry.
How does symmetry relate to conserved quantities in the universe?
-Symmetry relates to conserved quantities in the universe through the principle that every symmetry leads to a conserved quantity, such as the law of conservation of energy, momentum, and electric charge.
What is an example of symmetry in geometry and how does it illustrate the concept of group theory?
-An example of symmetry in geometry is an equilateral triangle, which has multiple lines of reflection and can be rotated 120 degrees to look identical. This illustrates the concept of group theory by showing how a set of transformations (like reflections and rotations) can generate all the symmetries of an object.
What is Noether's theorem and how does it connect symmetry with conservation laws?
-Noether's theorem states that for every symmetry there is a corresponding conservation law. This profound theorem directly connects symmetries with conserved quantities, such as time translation symmetry leading to the conservation of energy and space translation symmetry leading to the conservation of momentum.
How does the Dirac equation demonstrate the role of symmetry in quantum mechanics?
-The Dirac equation demonstrates the role of symmetry in quantum mechanics by showing how the equation for matter particles like electrons remains unchanged under certain symmetry transformations, such as U(1) symmetry, which is associated with the conservation of electric charge and the electromagnetic force.
What are the three fundamental symmetry groups respected by the standard model of particle physics, and what conservation laws do they correspond to?
-The three fundamental symmetry groups respected by the standard model are U(1), SU(2), and SU(3). They correspond to the conservation of electric charge, weak isospin (or weak charge), and color charge, respectively, and are associated with the electromagnetic, weak, and strong forces.
How do the U(1), SU(2), and SU(3) groups relate to the fundamental forces of nature?
-The U(1) group is associated with the electromagnetic force and the conservation of electric charge, mediated by the photon. The SU(2) group is associated with the weak force and the conservation of weak isospin, mediated by the W+, W-, and Z bosons. The SU(3) group is associated with the strong force and the conservation of color charge, mediated by eight different gluons.
What is the significance of generators in group theory?
-Generators in group theory are the basic elements that, through their combinations, produce all the elements of the group. They provide a concise way to describe a group and are analogous to the rules for transformations that preserve the symmetry of an object.
How does the concept of symmetry apply to complex numbers and the representation of a circle?
-The concept of symmetry applies to complex numbers and the representation of a circle through the use of polar coordinates and Euler's formula. A circle can be described with a single complex equation involving the angle phi, which shows how complex numbers can simplify and unify mathematical descriptions while preserving the underlying symmetry.
What is the role of the U(1) group in the context of quantum mechanics and electromagnetism?
-In the context of quantum mechanics and electromagnetism, the U(1) group is associated with the symmetry of rotations around a circle, which leads to the conservation of electric charge. The electromagnetic force is mediated by the photon, which is the force particle associated with the U(1) group's single generator.
How does the lecture series 'The Power of Symmetry' on Wondrium enhance the understanding of symmetry in physics?
-The lecture series 'The Power of Symmetry' on Wondrium, taught by Sean Carroll, enhances the understanding of symmetry in physics by exploring its fundamental role in the universe and its application in various physical theories, including quantum field theory, particle physics, and the search for the Higgs Boson.
Outlines
🔍 The Fundamental Role of Symmetry in Physics
This paragraph introduces the concept of symmetry as a core principle in physics, akin to detectives searching for clues about the universe's fundamental workings. It explains that symmetry leads to conserved quantities, such as energy, momentum, and electric charge, and is integral to understanding the laws of physics. The explanation begins with a simple example of symmetry using an equilateral triangle, demonstrating how symmetry can be observed through actions that do not change the object's inherent properties. The paragraph also introduces the concept of group theory, which is the mathematical framework behind the study of symmetry, and explains how it applies to the symmetries of geometrical shapes like triangles and squares.
📜 Group Theory and the Simplification of Complex Structures
This paragraph delves deeper into group theory, emphasizing its importance in simplifying the description of complex structures by using generators instead of listing all possible elements. It illustrates this with the example of a hexagon and how its symmetry can be described more succinctly using generators like rotations and reflections. The discussion moves on to the profound implications of group theory in physics, particularly in relation to Noether's theorem, which links symmetries to conservation laws. The paragraph also touches on the application of group theory in quantum mechanics and the role of complex numbers in describing circles and the U(1) group, setting the stage for understanding fundamental forces in physics.
🌀 The Emergence of Electromagnetic Force from U(1) Symmetry
This paragraph focuses on the application of U(1) symmetry in the context of the electromagnetic force. It explains how the absence of U(1) symmetry in the initial Dirac equation for fermions leads to a broken theory, which is then resolved by introducing a gauge field associated with the electromagnetic force. The paragraph describes how the addition of the electromagnetic field strength tensor and the photon field to the equation allows for electron interactions mediated by photons, leading to the formulation of quantum electrodynamics (QED). The conservation of electric charge is highlighted as a direct consequence of the U(1) symmetry, and the paragraph establishes the connection between gauge groups and the fundamental forces in the universe.
🌟 The Connection Between Symmetry Groups and Fundamental Forces
The final paragraph discusses the broader implications of symmetry groups in the standard model of particle physics, connecting U(1), SU(2), and SU(3) groups to the electromagnetic, weak, and strong forces, respectively. It explains how each group's symmetry leads to a conservation law and the corresponding force, with the number of generators in a group dictating the number of force-mediating particles. The paragraph also touches on the challenges of visualizing higher-dimensional symmetry groups and ends with a recommendation for a Wondrium course called 'The Power of Symmetry' by Sean Carroll, which provides an in-depth exploration of the topic. The video script concludes with a call to action for viewers to sign up for Wondrium and support the channel.
Mindmap
Keywords
💡Physicists
💡Symmetry
💡Noether's Theorem
💡Conservation Laws
💡Group Theory
💡Dihedral Group
💡Generators
💡Quantum Mechanics
💡Electromagnetic Force
💡Standard Model
💡Quantum Field Theory
Highlights
Physicists study the universe at its most fundamental level, akin to detectives searching for clues.
Symmetry is a core concept in physics and appears to be a fundamental property of the universe.
Every symmetry leads to a conserved quantity, such as the law of conservation of energy.
Symmetry in physics involves actions that don't visibly change anything, but transform the object while it looks the same.
Group theory is the mathematics behind symmetries, describing the operations that can be performed on a group.
The dihedral group of degree 3 represents the symmetries of an equilateral triangle, with 6 permutations.
Generators in group theory are operations that can produce all the elements of the group, simplifying complex structures.
Noether's theorem connects symmetries with conservation laws, stating that for every symmetry there is a corresponding conservation law.
Time translation symmetry leads to the conservation of energy, while space translation symmetry leads to the conservation of momentum.
The fundamental forces of nature arise from certain symmetries, such as the electromagnetic force from U(1) symmetry.
The Dirac equation describes the behavior of fermions, and when modified to respect U(1) symmetry, it introduces the electromagnetic force.
The electromagnetic force is mediated by the photon, which corresponds to the single generator of the U(1) group.
The standard model is constructed to respect symmetries represented by U(1), SU(2), and SU(3) groups, leading to conservation laws and fundamental forces.
The SU(2) group, associated with weak isospin conservation, leads to the weak force mediated by three bosons: W+, W-, and Z.
The SU(3) group, with conservation of color charge, is associated with the strong force mediated by eight gluons.
Symmetries are the foundation of the laws of physics, although the reason for this is not fully understood.
The U(1) group can be visualized as a one-dimensional sphere (circle) in two dimensions, while SU(2) and SU(3) groups are more complex and higher-dimensional.
Each generator of a gauge group corresponds to a force-mediating particle, such as the photon for the U(1) group.
Wondrium offers a course called 'The Higgs Boson and Beyond' taught by Sean Carroll, covering topics from quantum field theory to particle physics and symmetry.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: