Is ACTION The Most Fundamental Property in Physics?
TLDRThe video script explores the Principle of Least Action, a fundamental concept in physics that suggests everything in nature occurs in a way that minimizes or maximizes 'Action'. From Heron of Alexandria's observation of light's path to Fermat's principle of least time, the script delves into the evolution of this principle through Lagrange and Euler's contributions to Lagrangian mechanics. It further discusses the principle's application in Einstein's General Theory of Relativity and quantum mechanics, highlighting its significance in understanding the universe's fundamental nature.
Takeaways
- 🔍 The concept of the Principle of Least Distance was first proposed by Heron of Alexandria, which states that light travels the shortest path between two points.
- 💡 Pierre de Fermat later refined this principle by suggesting that light travels the path of least time, not distance, leading to the Principle of Least Time in optics.
- 🌐 Isaac Newton's laws of motion provided a way to calculate the exact positions, velocities, and accelerations of particles, but these calculations can be complex for intricate systems.
- 🚀 Joseph-Louis Lagrange introduced the concept of Action, which is the time-averaged difference between kinetic and potential energy, leading to the Principle of Least Action.
- 📈 Lagrange's work simplified the understanding of motion by focusing on energy rather than vectors, and led to the development of Lagrangian mechanics.
- 🔄 The Principle of Least Action was later corrected by William Hamilton to include both minimization and maximization of Action, known as the Stationary Action Principle.
- 🌌 Einstein's General Theory of Relativity further validated the Principle of Least Action by showing that the motion of planets, like Mercury, could be described using the relativistic version of Action based on proper time.
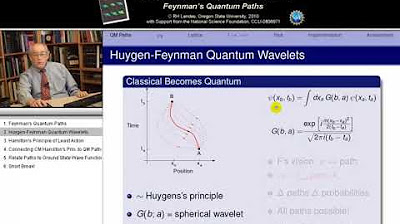
- 🤹 Paul Dirac and Richard Feynman contributed to the understanding of quantum mechanics through the concept of quantum action, which involves the integration of all possible paths a particle can take.
- 🎲 Feynman's path integral formulation of quantum mechanics aligns with the Principle of Least Action, suggesting that particles tend to follow paths that minimize or maximize quantum action.
- 🔗 The concept of configuration space is introduced as the space of all possible trajectories given an object's constraints, which is central to understanding the Principle of Least Action in both classical and quantum mechanics.
- 🌟 The development of the Standard Model Lagrangian, which describes the evolution of all quantum fields, is rooted in the understanding of Action and its application to the evolution of quantum states.
Q & A
What is the Principle of Least Distance proposed by Heron of Alexandria?
-The Principle of Least Distance proposed by Heron of Alexandria suggests that light, when moving between two points, follows the shortest path.
How did Pierre de Fermat refine the understanding of light's path?
-Pierre de Fermat refined the understanding by proposing that light doesn't necessarily travel the path of least distance, but rather the path of least time, which could explain refraction and other phenomena where light doesn't travel in a straight line.
What is the Principle of Least Action, and how did it emerge?
-The Principle of Least Action is a fundamental principle in physics stating that the path taken by a system between two states is the one that minimizes or maximizes the action. It emerged from the work of Joseph-Louis Lagrange, who found that a particular combination of kinetic and potential energy minimized over time, similar to Fermat's principle for light.
What is the Euler-Lagrange equation, and how does it relate to the Principle of Least Action?
-The Euler-Lagrange equations are mathematical equations derived by Euler and Lagrange that allow for the calculation of the path that minimizes the action. They are used in conjunction with the Principle of Least Action to determine the trajectories of particles and the behavior of physical systems.
How does the Principle of Least Action apply in the context of Einstein's General Theory of Relativity?
-In the context of General Relativity, the Principle of Least Action is applied by considering the proper time experienced by an object in its own reference frame. This relativistic version of the action allows for the correct prediction of planetary orbits, such as Mercury's orbit around the Sun.
What is the significance of the quantum action in quantum mechanics?
-The quantum action, as understood by Paul Dirac and Richard Feynman, is related to the integrated time evolution of the wavefunction. It plays a crucial role in the path integral formulation of quantum mechanics, where the most likely outcomes correspond to paths where the quantum action varies slowly, near its stationary points.
How does the concept of configuration space relate to the Principle of Least Action?
-Configuration space is the space of all possible trajectories given an object's constraints. In the context of the Principle of Least Action, the principle states that particles tend to follow paths that minimize the action in configuration space, which can be through space, spacetime, or more abstract quantum state spaces.
What is the Standard Model Lagrangian, and how does it connect to the history of the Principle of Least Action?
-The Standard Model Lagrangian is a mathematical description that combines the Lagrangians for each quantum field, allowing for the tracking of all quantum fields through configuration space and the prediction of the behavior of all known particles. It is a direct result of the application of the Principle of Least Action to quantum field theory.
How did the concept of action evolve from classical mechanics to modern theories?
-The concept of action evolved from being a somewhat vague notion of change in energy in classical mechanics to a more precise measure in relativity as the integral over proper time. In quantum mechanics, it further evolved into a quantum action that determines the likelihood of outcomes based on the phase shifts along various paths.
What is the significance of the path integral formulation in quantum mechanics?
-The path integral formulation of quantum mechanics, introduced by Richard Feynman, is a revolutionary approach that considers all possible paths a particle can take and sums their contributions weighted by the quantum action. This formulation reproduces the predictions of other quantum theories and provides a new perspective on how particles move and interact.
How does the Principle of Least Action relate to the double-slit experiment in quantum mechanics?
-In the double-slit experiment, the Principle of Least Action suggests that particles should land at points where the action of the trajectory is at a minimum or maximum. However, particles are found at all locations, with probabilities that peak near the stationary points of the quantum action, indicating a more complex relationship between action and quantum outcomes.
Outlines
🌟 The Principle of Least Action and its Discovery
This paragraph introduces the concept of the Principle of Least Action, highlighting its significance in physics. It begins with a historical account of Heron of Alexandria's observation that light travels the shortest path between two points, which was later refined by Pierre de Fermat's principle of least time. The discussion then moves to Isaac Newton's laws of motion and the complexity they introduce, leading to Joseph-Louis Lagrange's discovery that a particular combination of kinetic and potential energy minimizes the Action, leading to the Principle of Least Action. The paragraph emphasizes the search for a simple guiding principle in nature and the evolution of this principle through the works of great minds in physics.
🚀 Application of the Principle of Least Action in Modern Physics
The second paragraph delves into the application of the Principle of Least Action beyond classical mechanics, exploring its relevance in general relativity and quantum mechanics. It discusses Einstein's General Theory of Relativity and how the principle helps explain Mercury's orbit, introducing the concept of proper time. The paragraph also touches on the quantum realm, discussing the double-slit experiment and the wavefunction representing all possible paths a particle could take. It highlights the work of Paul Dirac and Richard Feynman, who contributed to understanding the quantum action and its role in determining a particle's path through the path integral formulation of quantum mechanics.
🧠 Deepening Understanding of Action through Quantum Mechanics
This paragraph continues the exploration of the Principle of Least Action in quantum mechanics, focusing on the path integral formulation and its implications. It explains how Richard Feynman's approach to quantum mechanics involves considering all possible paths a particle could take, weighted by the quantum action. The paragraph clarifies that in quantum mechanics, the action is not based on kinetic and potential energy or proper time, but on the phase shift a particle experiences along each path. It also introduces the concept of configuration space, which is the space of all possible trajectories given an object's constraints, and discusses how this concept ties together various aspects of physics, from classical to relativistic to quantum.
🤝 Community Insights on Constructor Theory and Physics
The final paragraph shifts focus to community engagement and discussion on the recent episode about constructor theory. It acknowledges the mixed reactions from the audience, with some finding it contentious and others seeing value in the exploration of this philosophical framework. The discussion includes various perspectives from viewers, such as the comparison of constructor theory to category theory and the potential of constructor theory to narrow down the search for physical laws. The paragraph also touches on the historical context of scientific discovery and the spirit of exploration, drawing parallels with Isaac Newton's alchemical pursuits and the potential for constructor theory to be a revolutionary concept or simply another step in the ongoing journey of understanding the universe.
Mindmap
Keywords
💡Principle of Least Distance
💡Pierre de Fermat
💡Lagrangian Mechanics
💡Action
💡Euler-Lagrange Equations
💡General Relativity
💡Quantum Mechanics
💡Feynman's Path Integral
💡Configuration Space
💡Standard Model Lagrangian
💡Constructor Theory
Highlights
The discussion of an obscure concept in physics that may be more fundamental than energy, entropy, and time itself.
Heron of Alexandria's observation in 40 AD that light follows the shortest path between two points, leading to the Principle of Least Distance.
Pierre de Fermat's proposal that light travels the path of least time, which deviates from the straight line in cases of refraction and gravitational fields.
The search for a similar property to momentum and kinetic energy that could determine the trajectories of matter, which was unsuccessful.
Isaac Newton's laws of motion that provided the ability to explain the motion of all particles in the universe based on exact vector forces.
Joseph-Louis Lagrange's discovery of a principle using energy instead of vectors, which states that a body will follow the path that minimizes the time-averaged difference between kinetic and potential energy.
The introduction of the term 'Action' to describe the integral over time of the difference between kinetic and potential energies.
The Principle of Least Action, which suggests that everything in nature happens in a way that minimizes or maximizes action.
The Euler-Lagrange equations, which are essential for applying the Principle of Least Action and lead to Lagrangian mechanics.
The transition from Newtonian mechanics to Lagrangian mechanics, which simplifies complex equations by focusing on energies rather than forces and vectors.
The application of the Principle of Least Action in Einstein's General Theory of Relativity, which describes gravity through the bending of space-time fabric.
The importance of proper time in relativistic corrections, which is the time perceived by an object in its own reference frame.
The revelation that action is the integral over proper time, simplifying the concept from a change in energy to the time measured on a path.
The exploration of quantum mechanics and the double-slit experiment, which challenges the Principle of Least Action with its interference patterns.
Paul Dirac's insight into a quantum analog of action related to the integrated time evolution of the wavefunction.
Richard Feynman's path integral formulation of quantum mechanics, which involves adding together all possible paths weighted by quantum action.
The concept of configuration space, which is the space of all possible trajectories given an object's constraints and plays a crucial role in understanding the action principle.
The Standard Model Lagrangian, derived from combining Lagrangians for each quantum field, allowing the tracking of all quantum fields through configuration space.
The journey from Heron of Alexandria's study of light to the development of modern quantum theory, illustrating the enduring impact of seeking fundamental patterns in nature.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: