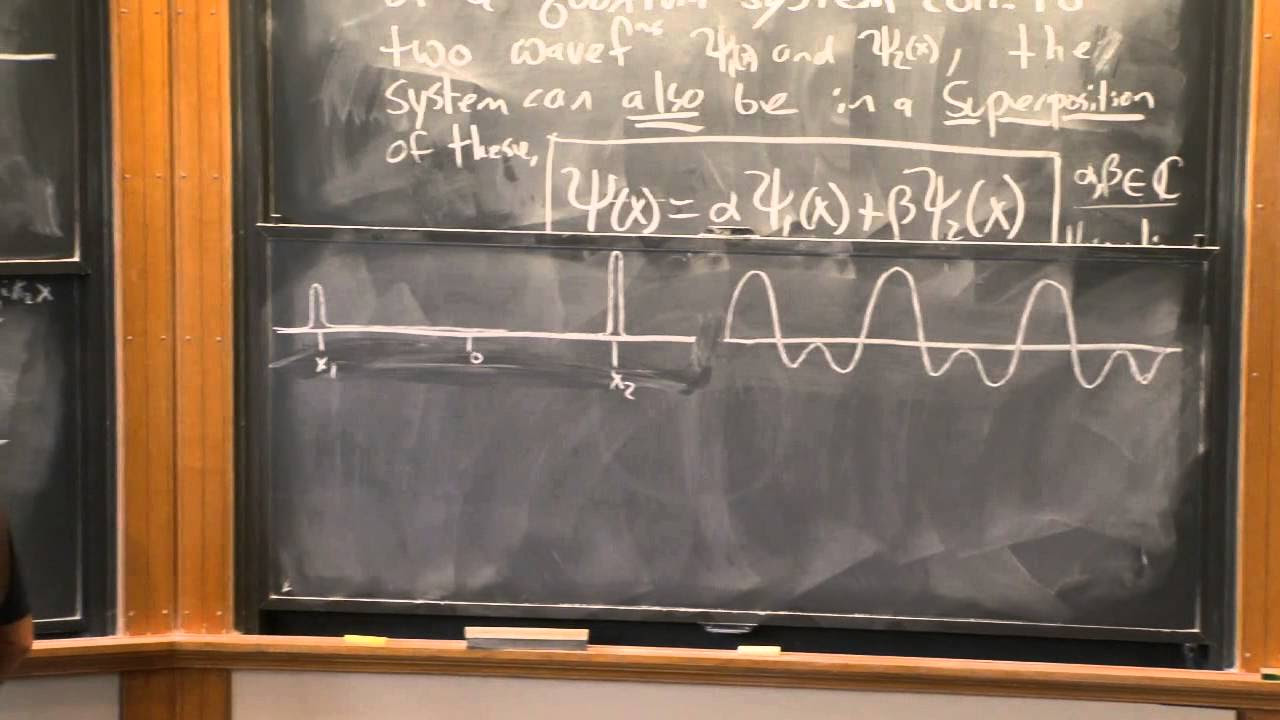What is the Heisenberg Uncertainty Principle? A wave packet approach
TLDRThe video delves into the quantum mechanical description of a freely moving particle, highlighting the profound implications of Heisenberg's uncertainty principle. It explains how the principle, which states that the exact position and momentum of a particle cannot be known simultaneously, emerges from the wave-particle duality of quantum objects. The video illustrates the construction of a localized wave packet through the superposition of multiple waves with varying wavelengths, leading to a Gaussian probability distribution that describes the likelihood of finding a particle at a certain location. The discussion extends to the time evolution of wave packets, emphasizing the inherent probabilistic nature of quantum mechanics and the continuous expansion of a particle's probability distribution over time.
Takeaways
- 🌟 The question of describing a freely moving particle in quantum mechanics leads to the introduction of Heisenberg's uncertainty principle.
- 📈 De Broglie proposed that particles like electrons can exhibit wave-like behavior, leading to the concept of wave-particle duality.
- 🌊 The initial attempt to describe a quantum particle using a plane wave function results in issues regarding wave velocity and non-normalizability.
- 🚀 The principle of superposition is used to create a localized wave function by combining multiple waves with slightly different wavelengths.
- 🌀 The group velocity of a wave packet is shown to be equal to the velocity of the particle it represents, resolving the issue of the plane wave's incorrect velocity.
- 📊 Gaussian modulation of the amplitudes of component waves in a superposition leads to a well-defined, isolated wave packet.
- 📈 The width of the wave packet is related to the uncertainty in the particle's position, while the range of wave numbers corresponds to the uncertainty in momentum.
- 🔄 The product of the uncertainties in position (Δx) and momentum (Δp) is found to be equal to a constant, specifically, the reduced Planck's constant divided by 2,体现Heisenberg's uncertainty principle.
- 🕒 Time dependence is introduced into the wave function, showing that as time progresses, the wave packet spreads out, increasing the uncertainty in the particle's location.
- 🌐 The time evolution of the wave packet is given by a time-dependent wave function, which maintains the same form as the time-independent wave function with specific substitutions.
- 🎓 The video concludes by highlighting the deep connection between the probabilistic description of particles in quantum mechanics and the fundamental limitations imposed by Heisenberg's uncertainty principle.
Q & A
What is the main question the video aims to answer?
-The main question the video aims to answer is how to describe the motion of a freely moving particle in the context of quantum mechanics.
What is Heisenberg's uncertainty principle?
-Heisenberg's uncertainty principle states that it is impossible to simultaneously know the exact location and momentum of a particle, implying a fundamental limit to our knowledge of the physical universe.
What did Louis de Broglie propose about particles and waves?
-Louis de Broglie proposed that if light waves can behave like particles (photons), then it is possible that particles such as electrons can behave like waves, leading to the concept of wave-particle duality.
What is the relationship between a particle's wavelength and its momentum according to de Broglie?
-According to de Broglie, the wavelength (Lambda) of a particle with mass (m) moving at velocity (v) is related to its momentum (p) by the equation Lambda = h/p, where h is Planck's constant.
What is the issue with using a plane wave function to describe a freely moving particle?
-The issue with using a plane wave function to describe a freely moving particle is that the wave function leads to an incorrect velocity (half the speed of the particle) and a non-normalizable wave function, which does not represent a physically realizable state.
How can a localized wave function be created?
-A localized wave function can be created by adding together multiple waves with slightly different wavelengths using the principle of superposition, which results in the formation of a wave packet.
What is the significance of the group velocity of a wave packet?
-The group velocity of a wave packet is significant because it represents the velocity at which the wave packet as a whole moves, which is equal to the velocity of the particle it is meant to represent.
How does the width of a wave packet relate to the uncertainty in the particle's position?
-The width of a wave packet is related to the uncertainty in the particle's position (Δx) such that as the width of the wave packet increases, the uncertainty in the particle's position also increases, and vice versa.
What is the mathematical expression for a Gaussian wave packet?
-The mathematical expression for a Gaussian wave packet is given by the integral involving a Gaussian amplitude function and a cosine term, which, when solved, results in a wave function that has a Gaussian probability density distribution in position space.
How does the time-dependent wave function of a particle evolve?
-The time-dependent wave function of a particle evolves by spreading and widening as it moves through space, with the width of the wave packet increasing over time due to the uncertainty in the particle's velocity.
What does the evolution of a wave packet over time indicate about the particle's position uncertainty?
-The evolution of a wave packet over time indicates that the uncertainty in the particle's position increases with time, reflecting the fact that as the wave packet spreads, the probability distribution of finding the particle in a particular location becomes broader.
Outlines
🌌 Introduction to Quantum Mechanics and the Heisenberg Uncertainty Principle
The video begins with the intention to explain how a freely moving particle is described in quantum mechanics. It introduces the profound concept of the Heisenberg uncertainty principle, which states that it's impossible to simultaneously know a particle's exact position and velocity. This principle revolutionized our understanding of the fundamental laws of physics and is central to quantum mechanics.
📐 De Broglie's Hypothesis and the Wave-Particle Duality
The script discusses Louis de Broglie's hypothesis from 1923, which proposed that particles like electrons could exhibit wave-like behavior. De Broglie suggested a relationship between a particle's mass, momentum, and the wavelength of the associated wave, which was later instrumental in the development of Schrödinger's wave equation. The video then shifts focus to describe the motion of a freely moving particle using wave functions.
🌠 The Problem with Plane Waves and the Need for Wave Packets
The video explains the limitations of using plane waves to describe particles. It points out that plane waves lead to incorrect velocity and non-normalizable wave functions, which are not physically meaningful. To overcome these issues, the concept of wave packets, created by superposing multiple waves with slightly different wavelengths, is introduced. The video then delves into the mathematical details of constructing and analyzing wave packets.
🚀 Group Velocity of Wave Packets and the Representation of a Free Particle
The script discusses the group velocity of wave packets and how it equals the velocity of the particle they represent. It explains the process of creating a localized wave packet through the superposition of multiple waves with varying wavelengths. The video also touches on the concept of normalizability and the importance of the wave function's modulus squared in providing probabilistic information about the particle's location.
📈 Gaussian Wave Packets and the Localization of Particles
The video continues with the construction of a localized wave packet using a Gaussian distribution of amplitudes. It explains how the superposition of a continuous spectrum of wave numbers with modulated amplitudes results in a well-defined, isolated wave packet. The script then discusses the removal of side lobes from the wave packet by modulating the amplitudes and the probabilistic interpretation of the wave function.
🧬 The Heisenberg Uncertainty Principle and Gaussian Distributions
The video connects the construction of Gaussian wave packets to the Heisenberg uncertainty principle. It explains how the product of the uncertainties in position (Δx) and momentum (Δp) is equal to a constant, which is related to the reduced Planck's constant divided by two. The script also discusses the mathematical properties of Gaussian distributions and their normalization, emphasizing their role in quantum mechanics.
🌟 Time Evolution of Wave Packets and the Spreading Effect
The video concludes by discussing the time-dependent behavior of wave packets. It explains how the width of the wave packet increases with time due to the uncertainty in the particle's velocity, leading to a spreading effect. The script then presents the time-dependent wave function and its implications, highlighting that the wave function provides information about the probability of finding a particle at a particular location, not the actual spreading of the particle itself.
Mindmap
Keywords
💡Quantum Mechanics
💡Heisenberg's Uncertainty Principle
💡Wave Function
💡Wave Packet
💡De Broglie Hypothesis
💡Schrodinger Equation
💡Probability Distribution
💡Momentum
💡Gaussian Distribution
💡Group Velocity
Highlights
Exploring the description of a freely moving particle in quantum mechanics leads to the discovery of Heisenberg's uncertainty principle.
De Broglie proposed that particles like electrons can exhibit wave-like behavior, leading to the connection between particle properties and wave characteristics.
The wave-particle duality of matter is demonstrated through the relation between wavelength, momentum, and energy of a particle.
A plane wave function fails to accurately represent a freely moving particle due to incorrect velocity and non-normalizability issues.
The principle of superposition is used to create a localized wave function, which can represent a particle more accurately.
A wave packet is constructed by combining multiple waves with slightly different wavelengths, leading to a group velocity that matches the particle's velocity.
The group velocity of a wave packet is shown to be equal to the velocity of the particle it represents, providing a consistent description of motion.
The concept of wave packet localization is introduced to improve the spatial probability distribution of finding a particle.
Gaussian modulation of wave amplitudes results in a more defined wave packet, reducing unwanted fluctuations.
The mathematical description of a Gaussian wave packet is derived, revealing its probabilistic nature in quantum mechanics.
The modulus squared of the wave function provides the probability density distribution for finding a particle in a particular location.
The uncertainty principle is derived from the wave packet analysis, showing a fundamental limit to the knowledge of a particle's position and momentum.
The time evolution of a wave packet is discussed, explaining how its width increases as it propagates through space.
The time-dependent wave function is obtained, allowing for the analysis of a particle's behavior over time in quantum mechanics.
The spreading of a wave packet with time illustrates the increase in the uncertainty of a particle's location.
Heisenberg's uncertainty principle is reaffirmed as a fundamental concept in quantum mechanics, highlighting the probabilistic nature of particles.
The video concludes with a reflection on the limitations of scientific understanding and the continuous journey into the unknown.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: