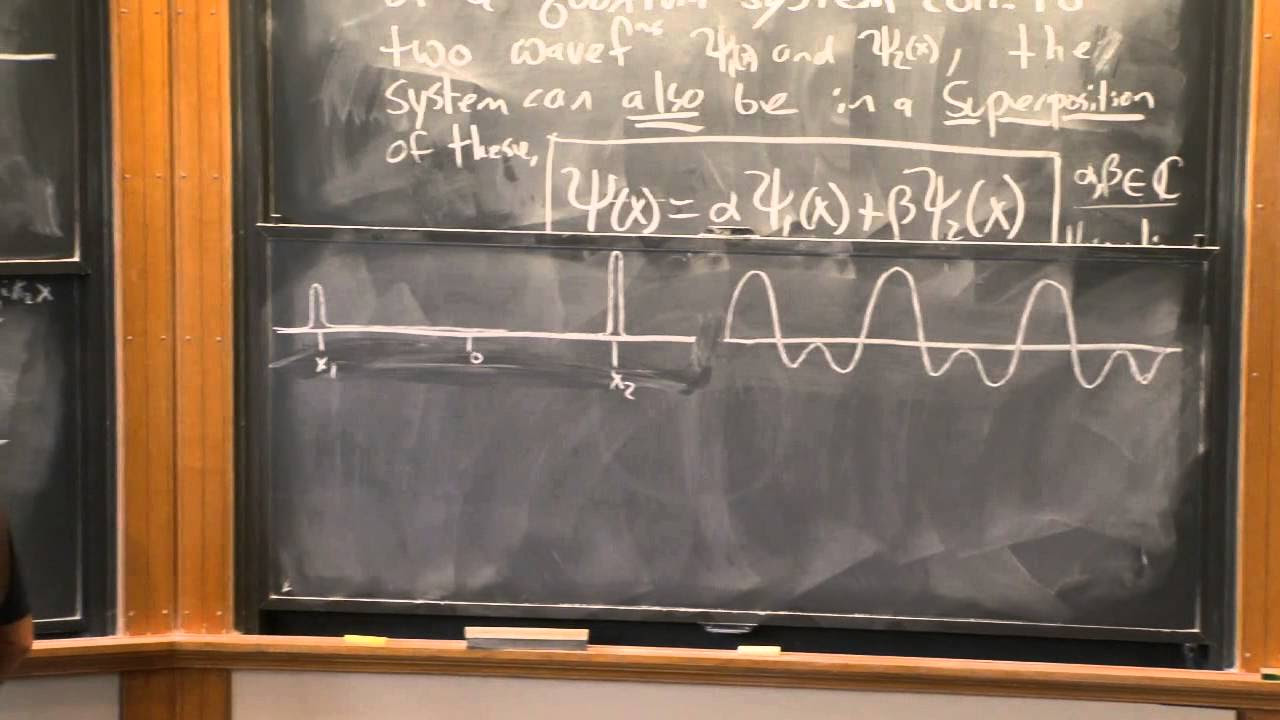The Quantum Wavefunction Explained

Domain of Science
17 Apr 202105:39
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of wave functions in quantum mechanics, emphasizing their mathematical nature and their role in describing particle behavior. It explains that while wave functions are not directly observable, they are essential for calculating probabilities related to a particle's position and other physical properties. The script also touches on the conditions that wave functions must meet, such as being a solution to the Schrödinger equation, normalizable, single-valued, and continuous. The concept of superposition is introduced, highlighting the idea that quantum states can exist in multiple states simultaneously, a phenomenon central to interpretations of quantum mechanics.

Takeaways
  • 🌊 Quantum mechanics describes particles' behavior through wave functions, satisfying the Schrödinger equation.
  • 📈 Wave functions are mathematical tools used in various systems, not just quantum mechanics, to describe wave-like phenomena.
  • 🌐 Quantum wave functions are not real physical waves like water ripples or electromagnetic waves; they lack a physical medium.
  • 🤔 The reality of wave functions is a subject of debate and interpretation within quantum mechanics.
  • 📊 A quantum wave function is a complex mathematical expression that can be visualized for easier understanding.
  • 🕒 The wave function depends on time and space, with simplifications made for visualization purposes.
  • 📏 The probability of finding a particle is determined by the modulus squared of the wave function's amplitude.
  • 🔄 A wave function encodes all measurable properties of a quantum particle, explaining the probabilistic nature of particle locations.
  • 🔗 Wave functions must satisfy the Schrödinger equation, be normalizable, single-valued, and continuous with a continuous gradient.
  • 🌟 Superposition allows for the combination of multiple valid wave functions, leading to the concept of particles being in multiple states simultaneously.
Q & A

  • What is the primary object described by the wave function in quantum mechanics?

    -The wave function in quantum mechanics primarily describes the behavior of particles, including their probabilities of being found in certain locations and other physical properties like momentum, energy, or spin.

  • How does the wave function relate to the Schrödinger equation?

    -The wave function satisfies the Schrödinger equation, which is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time.

  • Are wave functions only used in quantum mechanics?

    -No, wave functions are not unique to quantum mechanics. They are also used in other systems like the motion of ripples on water, sound waves, vibrations on a string, and electromagnetic waves, each with their own wave equation.

  • What is the key difference between quantum wave functions and other types of waves?

    -The key difference is that quantum wave functions are not real physical waves. Unlike other waves, there is no medium like water or an electromagnetic field that is wobbling, so we cannot say that quantum waves are real with our current knowledge because they cannot be measured directly.

  • What is the significance of the wave function being a probability amplitude?

    -The wave function itself is not a physical entity, but its square (mod squared) represents the probability of finding a particle at any point in space. This highlights the probabilistic nature of quantum mechanics.

  • What are the conditions that a wave function must meet?

    -A wave function must be a solution of the Schrödinger equation, normalizable (its integral over all space must equal 1), single-valued, continuous, and have a continuous gradient.

  • What is the concept of superposition in quantum mechanics?

    -Superposition in quantum mechanics refers to the idea that any linear combination of two or more valid wave functions, which satisfy the Schrödinger equation, is also a valid solution. This concept leads to states like Schrödinger's cat being both dead and alive simultaneously, although other quantum phenomena like entanglement and decoherence come into play in reality.

  • How can we visualize the wave function mathematically?

    -We can visualize the wave function by plotting its real and imaginary parts on separate axes, which can result in a spiral of complex values. However, for simplicity, often only a section of the wave function is plotted fixed at a particular point in time.

  • What does the variable 'k' in the wave function represent?

    -In the wave function, 'k' is a variable that controls the size of the wavelength of the cosine wave component.

  • What role does the imaginary number 'i' play in the quantum wave function?

    -The imaginary number 'i' is used in the sine part of the wave function, making it a complex wave function. This complexity is why it requires an additional axis for visualization, even though the wave is one-dimensional.

  • How does the wave function account for all measurable physical quantities?

    -The wave function is a mathematical tool that keeps track of all the properties of a quantum particle. By performing different mathematical operations on the wave function, one can extract information about various physical quantities such as position, momentum, energy, and spin.

Outlines
00:00
🌊 Quantum Mechanics and Wave Functions

This paragraph delves into the concept of quantum mechanics, focusing on the wave function that describes the behavior of particles. It explains that wave functions are solutions to the Schrödinger equation and are not unique to quantum mechanics, as they are used in various systems like water ripples, sound waves, and electromagnetic waves. The key difference highlighted is that quantum wave functions are not real physical waves, as there is no medium like water or an electromagnetic field involved. The paragraph also touches on the interpretation of wave functions in terms of probability amplitudes, which can be used to calculate the probability of finding a particle at any point in space. Additionally, it outlines the conditions that wave functions must meet, such as being a solution to the Schrödinger equation, normalizable, single-valued, continuous, and having continuous gradient. The concept of superposition is introduced, explaining how it allows for the coexistence of multiple states in quantum mechanics.

05:00
🎥 Video Acknowledgments and Further Resources

The second paragraph shifts focus from the technical aspects of quantum mechanics to acknowledge the support behind the creation of the video. It expresses gratitude to the patrons on Patreon and those who purchase items from the speaker's store, emphasizing that their support is crucial for the continuation of the channel. The paragraph also recommends an additional resource for viewers interested in exploring the subject further, directing them to an excellent video by Sabine Hosenfelder on the related topic of Schrödinger's cat, entanglement, and decoherence, which are beyond the scope of the current video.

Mindmap
Keywords
💡quantum mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the smallest scales, such as particles at the atomic and subatomic levels. It is characterized by the use of wave functions and the Schrödinger equation, which are central to understanding the probabilistic nature of quantum phenomena. In the video, quantum mechanics is the main subject, with the discussion revolving around the interpretation and visualization of wave functions and their implications for understanding particle behavior.
💡wave function
A wave function is a mathematical function that describes the quantum state of a particle or system in quantum mechanics. It contains all the information about the system and is used to calculate the probabilities of various physical properties, such as position, momentum, and energy. The wave function is not a physical wave but a mathematical representation that guides our understanding of quantum behavior. In the video, the wave function is visualized and explained as a key to interpreting the probabilistic nature of quantum particles.
💡Schrödinger equation
The Schrödinger equation is a fundamental partial differential equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is named after Austrian physicist Erwin Schrödinger and is essential for determining the wave function of a system. The video emphasizes the importance of the Schrödinger equation in defining the behavior of wave functions in quantum mechanics.
💡probability amplitude
In quantum mechanics, the probability amplitude is a complex number associated with a wave function that, when squared (mod squared), gives the probability of finding a particle in a particular state or at a specific location. It is not a physical entity on its own but is crucial for understanding the probabilistic outcomes of quantum events. The video clarifies that the wave function represents this probability amplitude, which is central to the interpretation of quantum phenomena.
💡normalizable
A wave function is said to be normalizable if its integral over all space converges to a finite value, which is a requirement for it to represent a physical state. This property ensures that the total probability of finding the particle anywhere in space is equal to one, adhering to the fundamental principle that probabilities must sum to 100%. Normalizability is one of the conditions that a valid quantum wave function must satisfy.
💡superposition
Superposition is a principle in quantum mechanics stating that a quantum system can be in multiple states simultaneously until it is measured. When two or more wave functions represent valid states of a system, any linear combination of these wave functions is also a valid state. This principle is key to understanding phenomena like Schrödinger's cat being both dead and alive until an observation is made, as mentioned in the video.
💡single-valued
In the context of quantum mechanics, a wave function must be single-valued, which means that for any given position in space, there is only one value of the wave function. This property ensures consistency and predictability in the mathematical description of quantum states and is one of the conditions that a valid wave function must meet.
💡continuous
Continuity in mathematics and physics means that a function does not have any gaps, jumps, or breaks in its graph. For a wave function in quantum mechanics to be physically meaningful, it must be continuous, ensuring a smooth transition of values across its domain. This is important for maintaining the integrity of the mathematical model and for making accurate predictions about quantum systems.
💡differentiable
Differentiability in mathematics refers to the property of a function that allows it to be differentiated, meaning it has a derivative at every point in its domain. In quantum mechanics, the wave function's differentiability is crucial because it ensures that the function's slope (gradient) is continuous, which is necessary for the wave function to satisfy the Schrödinger equation and accurately describe the quantum state.
💡interpretations of quantum mechanics
The interpretations of quantum mechanics refer to various philosophical and scientific perspectives on the meaning and implications of the theory's mathematical formalism. These interpretations attempt to explain phenomena such as wave-particle duality, superposition, and the measurement problem. The video touches on this topic when discussing the reality of the wave function and refers to different interpretations without delving into specifics.
💡visualization
Visualization in the context of the video refers to the graphical representation of complex mathematical concepts, such as the wave function, to aid in understanding. Since quantum wave functions cannot be seen directly, visualizing their mathematical form helps to convey their behavior and the probabilistic nature of quantum particles.
Highlights

In quantum mechanics, particles are only seen when measured, with their movement described by a wave function.

The wave function satisfies the Schrödinger equation, a fundamental equation in quantum mechanics.

Wave functions are not unique to quantum mechanics and are used in other systems like water ripples, sound waves, and electromagnetic waves.

Quantum wave functions are not real physical waves as there is no medium like water or an electromagnetic field.

The reality of the wave function is a subject of debate within the interpretations of quantum mechanics.

Visualization of the mathematical equations of the wave function is possible, even though the quantum wave function cannot be seen.

The wave function depends on time and one dimension of space, simplifying the complex three-dimensional reality.

The wave function is a complex function, involving the imaginary number i.

The wave function can be plotted, showing a spiral of complex values.

The wave function is called a probability amplitude, which is not physical on its own.

The mod squared of the amplitude gives the probability of finding a particle at any point in space.

The wave function provides information about all measurable physical quantities of a quantum particle.

A wave function must be a solution of the Schrödinger equation to be valid.

The wave function must be normalizable, meaning it cannot have an infinite area.

Quantum wave functions must be single-valued and continuous, with no breaks or discontinuities.

Superposition is a property of quantum mechanics where two or more wave functions can combine to form a valid solution.

The concept of superposition leads to ideas like Schrödinger's cat being both dead and alive simultaneously.

Other quantum phenomena like entanglement and decoherence affect the concept of superposition.

Transcripts

Browse More Related Video

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

25. Quantum Mechanics VII: Summary of postulates and special topics

Lecture 9 | The Theoretical Minimum

Lecture 5: Operators and the Schrödinger Equation

Lecture 3: The Wave Function

23. Quantum Mechanics V: Particle in a Box

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsWaveFunctionSchrodingerEquationProbabilityAmplitudeSuperpositionPhysicsExplainedQuantumBehaviorMathematicalToolsPhysicsEducationSandbox