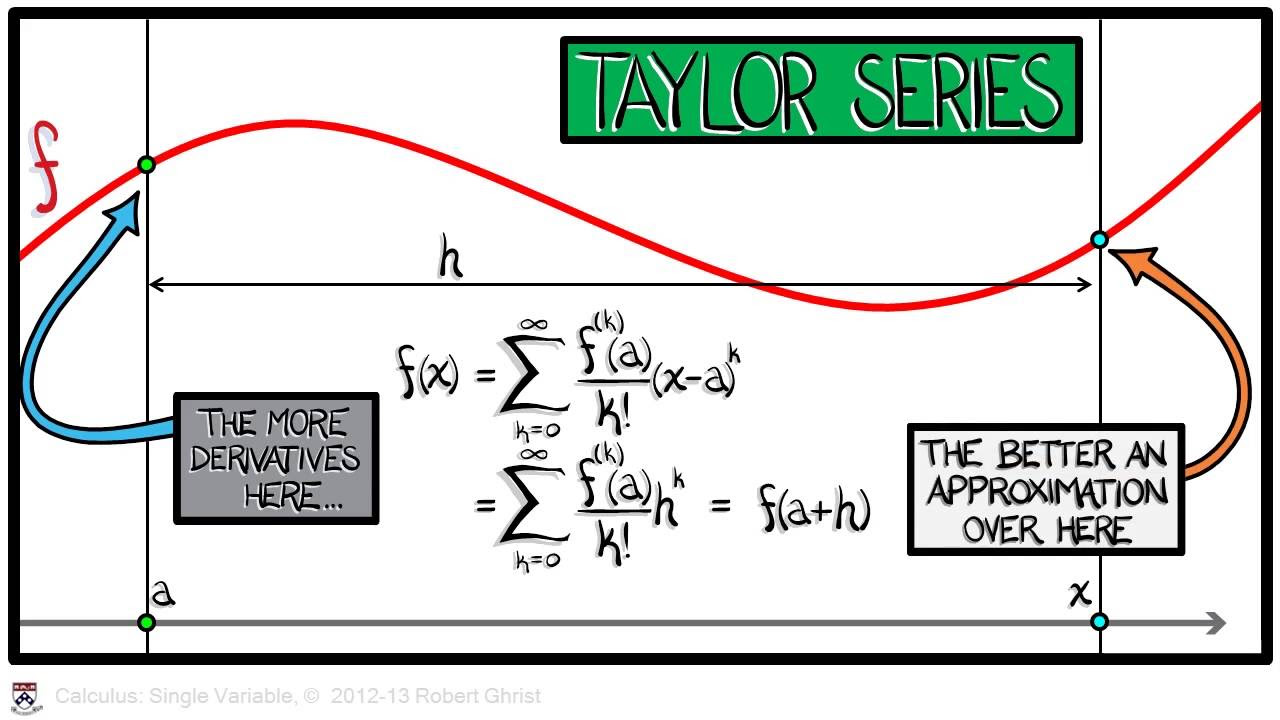
Integration of Taylor's Series | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this recitation, Professor Joel Lewis introduces a Taylor series with coefficients that form a linear polynomial. He challenges students to identify the underlying function, offering a hint to use calculus on Taylor series. The solution involves integrating the series term by term, revealing an antiderivative that resembles a familiar geometric series. The function is eventually identified as the derivative of 1/(1-x), with the series valid for x between -1 and 1. The video also touches on the concept of radius of convergence, emphasizing its invariance under differentiation and integration.
Takeaways
- 📚 The lecture is about Taylor series and their manipulations, with an example given that the students haven't seen in the lecture.
- 🔍 The task for the students is to identify the function represented by the given Taylor series: 1 + 2x + 3x^2 + 4x^3 + 5x^4, and so on.
- 🤔 The lecturer suggests using known tools for manipulating Taylor series, such as calculus operations like differentiation and integration.
- 📉 Differentiating the series results in a new series with coefficients that follow a quadratic polynomial pattern, complicating the situation.
- 📈 Integrating the series is straightforward and leads to a simpler expression, suggesting that integration might be a useful manipulation.
- 🌟 The lecturer introduces the series as 'f(x)' and integrates it term by term, resulting in a series that resembles a geometric series.
- 🎯 The integration leads to the conclusion that 'f(x)' is the derivative of 1/(1-x), a known geometric series.
- 📝 The choice of the constant of integration is highlighted as irrelevant because differentiation will eliminate it.
- 🧩 The final function form of 'f(x)' is derived as the derivative of 1/(1-x), which simplifies to 1/(1-x)^2 using the chain rule.
- 🔄 The process of verifying the derived function can be done by computing the power series for 1/(1-x)^2 or by squaring the geometric series.
- 📊 The radius of convergence for the series is discussed, noting that it remains unchanged after differentiation or integration and is valid between -1 and 1.
- 💡 The lecture concludes with a hint at further exploration, such as finding the function whose power series has coefficients following a quadratic polynomial.
Q & A
What is the main topic discussed in the recitation?
-The main topic discussed in the recitation is the manipulation of Taylor series and identifying the function represented by a given Taylor series.
What is the given Taylor series in the example?
-The given Taylor series is 1 + 2x + 3x^2 + 4x^3 + 5x^4, and so on, where the coefficients follow a linear polynomial pattern.
What hint does the instructor provide to help identify the function represented by the Taylor series?
-The instructor suggests using calculus on Taylor series, such as taking derivatives and integrals, to simplify the expression and identify the function.
What calculus operation does the instructor perform on the Taylor series to simplify it?
-The instructor performs integration on the Taylor series to find its antiderivative, which simplifies the expression and helps identify the function.
What is the antiderivative of the given Taylor series?
-The antiderivative of the given Taylor series is c + x + x^2 + x^3 + x^4 + ..., where c is the constant of integration.
Why does the instructor choose c to be 1 in the antiderivative?
-The instructor chooses c to be 1 because it leads to a familiar power series that is known to equal 1 / (1 - x), which simplifies the process of identifying the original function.
What familiar power series does the instructor recognize after setting c to 1?
-The instructor recognizes the power series 1 + x + x^2 + x^3 + x^4 + ..., which is known to be equal to 1 / (1 - x).
What is the function represented by the given Taylor series?
-The function represented by the given Taylor series is the derivative of 1 / (1 - x), which is 1 / (1 - x)^2.
How can one verify the identified function is correct?
-One can verify the identified function by computing a few terms of the power series for 1 / (1 - x)^2 using the derivative formula or by multiplying the polynomial (1 - x) by itself and comparing it to the original series.
What is the radius of convergence for the identified function?
-The radius of convergence for the identified function is between -1 and 1, as the series diverges at the endpoints.
Why does the radius of convergence remain the same after taking a derivative or antiderivative of a power series?
-The radius of convergence remains the same because these operations do not change the fundamental behavior of the series' convergence, only its value at the endpoints may be affected.
Outlines
📚 Introduction to the Taylor Series Problem
In this video script, Professor Joel Lewis introduces a unique Taylor series problem to his students. He presents a series that expands as 1 plus 2x plus 3x^2 and so on, with each term's coefficient increasing linearly. The challenge is to identify the function that this series represents. Lewis hints at using the students' knowledge of calculus and series manipulation to simplify the series into a recognizable form. He encourages students to apply their understanding of derivatives, integrals, and other algebraic operations to find the function. The video sets the stage for a deeper exploration of series manipulation and function identification.
🧩 Solving the Taylor Series Puzzle
After giving the students time to ponder the Taylor series, Professor Lewis proceeds to guide them through the solution. He suggests considering the calculus tools at their disposal, particularly differentiation and integration. By differentiating the series, the coefficients transform into a quadratic polynomial, which initially seems to complicate matters. However, Lewis cleverly shifts focus to integration, noting that the series has a straightforward antiderivative. He renames the series as f(x) and integrates term by term, resulting in a series that resembles a geometric series with a constant of integration. Lewis then chooses a convenient value for the constant, leading to the realization that the series is the derivative of 1/(1-x), a well-known geometric series. The function f(x) is thus identified as the derivative of 1/(1-x) squared, and Lewis demonstrates how to verify this by expanding the function into a power series or by squaring the geometric series. He also touches on the concept of radius of convergence, noting that it remains unchanged after differentiation or integration, and confirms the series' divergence at the endpoints of its interval of convergence.
Mindmap
Keywords
💡Taylor series
💡Differentiation
💡Integration
💡Coefficients
💡Antiderivative
💡Power series
💡Chain rule
💡Radius of convergence
💡Geometric series
💡Function manipulation
💡Derivative formula
Highlights
Introduction to the task of identifying a function from its Taylor series.
The given Taylor series is 1 + 2x + 3x^2 + 4x^3 + 5x^4, and so on.
The hint to use known tools to manipulate Taylor series, such as calculus operations.
Differentiation of the series results in coefficients that follow a quadratic polynomial pattern.
Integration of the power series is suggested as an easy manipulation to simplify the expression.
The antiderivative of the series is a power series with terms x, x^2, x^3, etc., plus a constant of integration.
Choosing a convenient value for the constant of integration, specifically c=1.
Recognition of a familiar power series pattern after integration, 1 + x + x^2 + x^3 + ...
The known formula for the series 1/(1-x) is related to the integrated form of the given series.
The function f(x) is identified as the derivative of 1/(1-x).
Differentiation of 1/(1-x) to find f(x) results in 1/(1-x)^2.
Verification of the derived function by computing its power series or multiplying the known series by itself.
Discussion on the radius of convergence and its invariance under differentiation and integration.
The series converges for x between -1 and 1, and diverges at the endpoints.
Application of the method to identify other power series by taking derivatives or integrals of known series.
Conclusion summarizing the approach to deducing the functional form of a power series.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: