What does Sin, Cos, Tan actually mean? Trigonometry explained for Beginners!
TLDRThe video script offers an insightful exploration of trigonometric functions—sine, cosine, and tangent—presenting them as abstract concepts rather than tangible objects. It explains their roles as functions, taking an angle as input and providing a ratio as output. The script creatively uses the analogy of a price tag to illustrate this concept and delves into mathematical notation, demonstrating how these functions are represented. A unit circle is introduced to visually depict how sine and cosine relate to horizontal and vertical shifts, respectively, and the tangent function is defined as the slope of a line. The video aims to provide a visual understanding of these concepts, moving beyond rote memorization to a deeper comprehension of their applications and significance in trigonometry.
Takeaways
- 📚 Sine, cosine, and tangent are nouns that represent mathematical functions, not tangible objects.
- 📈 These functions take an input (an angle) and provide an output (a ratio or value related to that angle).
- 🤔 The concept of 'price' is used as an analogy to explain functions, where the input is a product and the output is its cost.
- 📊 Mathematical notation for functions is expressed using the function name, input in parentheses, and an equals sign followed by the output.
- 🌐 The input for sine, cosine, and tangent functions is an angle measured in degrees, and the output is a numerical value.
- 📐 The unit circle is a circle with a radius of one, centered at the origin of the coordinate plane, and is used to visualize trigonometric functions.
- 🔄 As an angle moves around the unit circle, the horizontal shift corresponds to the cosine value and the vertical shift corresponds to the sine value.
- 🔢 Tangent is the ratio of the vertical shift (sine) to the horizontal shift (cosine), representing the slope of the radius line from the center to a point on the circle.
- 🚫 Tangent of 90 degrees is undefined because cosine of 90 degrees is zero, leading to division by zero.
- 📈 The values of sine and cosine for specific angles (like 30, 45, 60, 90 degrees) are explained with the help of the unit circle.
- 🎥 The video aims to provide a visual understanding of trigonometric functions, moving beyond just rote memorization of definitions.
Q & A
What are sine, cosine, and tangent in the context of this script?
-In the script, sine, cosine, and tangent are described as functions, not tangible objects. They are used to represent the relationship between an angle and its corresponding values in trigonometry.
How does the script explain the concept of a noun in mathematics?
-The script explains that while nouns typically refer to tangible objects, some nouns in mathematics represent concepts or relationships, such as 'price' or 'function', which are not physical entities.
What is the role of a unit circle in trigonometry?
-The unit circle is central to understanding sine, cosine, and tangent. It is a circle with a radius of one, centered at the origin of the coordinate plane. The horizontal and vertical shifts from the center to any point on the circle represent the cosine and sine values of the angle, respectively.
How are sine, cosine, and tangent functions represented in mathematical notation?
-In mathematical notation, sine, cosine, and tangent functions are represented with the function name followed by parentheses enclosing the input value. For example, sin(30°) represents the sine of 30 degrees.
What is the significance of angles in trigonometric functions?
-Angles are the input values for trigonometric functions like sine, cosine, and tangent. They are used to calculate the corresponding output values, which represent the ratios of the sides in a right-angled triangle or the shifts on the unit circle.
How does the script explain the concept of a function in mathematics?
-The script explains a function as a relationship where one value (the input) determines another value (the output). In the context of trigonometry, the input is an angle, and the output is a value related to that angle's position on the unit circle.
What is the tangent function in trigonometry?
-The tangent function, denoted as tan, is the ratio of the vertical shift (sine) to the horizontal shift (cosine) of a point on the unit circle at a given angle. It represents the slope of the line drawn from the center of the circle to the point on the circle.
Why does the tangent of 90 degrees give an error?
-The tangent of 90 degrees gives an error because the cosine value, which represents the horizontal shift, is zero at this angle. Dividing by zero (as in the rise over run calculation for slope) is undefined, leading to an error.
How does the script illustrate the relationship between trigonometric functions and right-angled triangles?
-The script connects the concepts by showing that the horizontal and vertical shifts on the unit circle correspond to the sides of a right-angled triangle, with sine representing the ratio of the opposite side to the hypotenuse and cosine representing the ratio of the adjacent side to the hypotenuse.
What is the significance of the 45-degree angle in trigonometry?
-At a 45-degree angle on the unit circle, the horizontal and vertical shifts are equal, meaning sine and cosine values are the same. This results in the tangent value being 1, as the rise and run of the slope calculation are equal.
How does the script suggest further learning in trigonometry?
-The script suggests that further learning in trigonometry can be achieved by visual understanding and practical application of concepts, as well as watching more videos on the subject, which the speaker plans to post on their channel.
Outlines
📚 Introduction to Trigonometric Functions
The paragraph introduces the concept of trigonometric functions, specifically sine, cosine, and tangent, as nouns that represent abstract mathematical functions rather than tangible objects. It draws an analogy with the concept of 'price' as a function, explaining that just like 'price', these functions take an input and produce an output. The input for these functions is an angle, and the output is a numerical value. The explanation includes the idea of angles and how they relate to the unit circle, emphasizing that these functions are not physical objects but mathematical concepts.
📝 Mathematical Notation and Functions
This paragraph delves into the mathematical notation used for functions, using the example of the 'price' function to illustrate how inputs and outputs are represented. It then applies this notation to sine, cosine, and tangent functions, showing how angles are used as inputs. The paragraph also introduces the concept of an open function, where the input is represented by a variable (like 'x' or 'θ'), which can take any value within a specified range, such as 0 to 360 degrees for angles.
📐 The Unit Circle and Trigonometric Functions
The explanation shifts to the unit circle, a visual tool used to understand sine, cosine, and tangent functions. The unit circle is defined and its relationship to angles and their corresponding coordinates (x and y) is explored. The paragraph describes how moving a point around the unit circle at various angles (45, 90, 135, 180, 270, and 70 degrees) results in different x and y coordinates, which correspond to the cosine and sine of those angles, respectively.
🔄 Understanding Angle Positions on the Unit Circle
This section continues the exploration of angles on the unit circle, focusing on how the position of an angle (magnet) affects its x and y coordinates. The explanation includes a detailed look at how the horizontal (x) and vertical (y) shifts of the magnet correspond to the cosine and sine values, respectively. The paragraph provides examples of calculating these values at different angles, such as 45, 90, 180, and 270 degrees, and emphasizes the relationship between the unit circle and the trigonometric functions.
📌 Trigonometric Functions and the Unit Circle
The paragraph further clarifies the connection between the unit circle and trigonometric functions. It explains how the horizontal shift on the unit circle represents the cosine of an angle, while the vertical shift represents the sine. The explanation includes practical examples of calculating cosine and sine values for various angles, reinforcing the concept with visual and numerical information. The paragraph also touches on the periodic nature of these functions, as seen when the angle reaches 360 degrees and returns to its starting point.
📈 Visualizing Trigonometric Functions with the Unit Circle
This paragraph visually connects the concepts of sine and cosine with the unit circle, transitioning into a discussion on the tangent function. It explains the tangent function as the slope of the line drawn from the center of the unit circle to a point on the circle, which is determined by the angle. The paragraph uses the unit circle to demonstrate how the tangent of an angle is calculated as the ratio of sine to cosine. The explanation includes examples and highlights the undefined nature of the tangent function at 90 degrees due to division by zero.
🎓 Conclusion and Future Trigonometry Lessons
The paragraph concludes the video script by summarizing the visual understanding of trigonometric functions presented in the video. It emphasizes the practical application of the unit circle in understanding sine, cosine, and tangent, and how this knowledge can enhance the learning experience beyond mere memorization. The speaker expresses hope that the video has been helpful and encourages viewers to subscribe for more content on trigonometry and other mathematical concepts.
Mindmap
Keywords
💡Trigonometry
💡Sine
💡Cosine
💡Tangent
💡Unit Circle
💡Right-Angled Triangle
💡Function
💡Variable
💡Graph
💡Coordinate Plane
💡Degree
Highlights
Sine, cosine, and tangent are nouns that represent mathematical functions, not tangible objects.
These functions can be thought of as relationships, similar to the concept of 'price' relating a product to its cost.
In mathematics, sine, cosine, and tangent functions take an angle as input and produce a numerical output.
Angles can range from 0 to 360 degrees and are used as inputs for these trigonometric functions.
The mathematical notation for these functions uses the name of the function, followed by an input in parentheses, and an equals sign with the output.
A variable, often 'x' or the Greek letter 'theta', is used to represent an unspecified input value for the function.
The unit circle, a circle with a radius of one centered at the origin of the coordinate axes, is key to understanding sine and cosine.
The horizontal shift from the center of the unit circle represents the cosine of the angle, while the vertical shift represents the sine.
Tangent is defined as the ratio of the vertical shift to the horizontal shift, or equivalently, sine divided by cosine.
At 0 degrees, the tangent is 0 because there is no rise (vertical shift), and the run (horizontal shift) is 1.
At 90 degrees, the tangent function is undefined because the cosine (horizontal shift) is 0, and division by zero is not possible.
At 45 degrees, the tangent is 1 because the rise (sine) equals the run (cosine), making the ratio 1.
The concepts of sine, cosine, and tangent are visually demonstrated using a magnet rotating around a unit circle to show the corresponding shifts.
The relationship between angles and their corresponding sine, cosine, and tangent values is foundational to trigonometry.
This visual approach aims to provide a better understanding of trigonometric functions rather than just memorization.
The video provides a practical application of sine, cosine, and tangent by connecting their abstract definitions to a right-angled triangle.
The content is designed to supplement and enhance understanding of trigonometry for students and those interested in mathematics.
Transcripts
Browse More Related Video
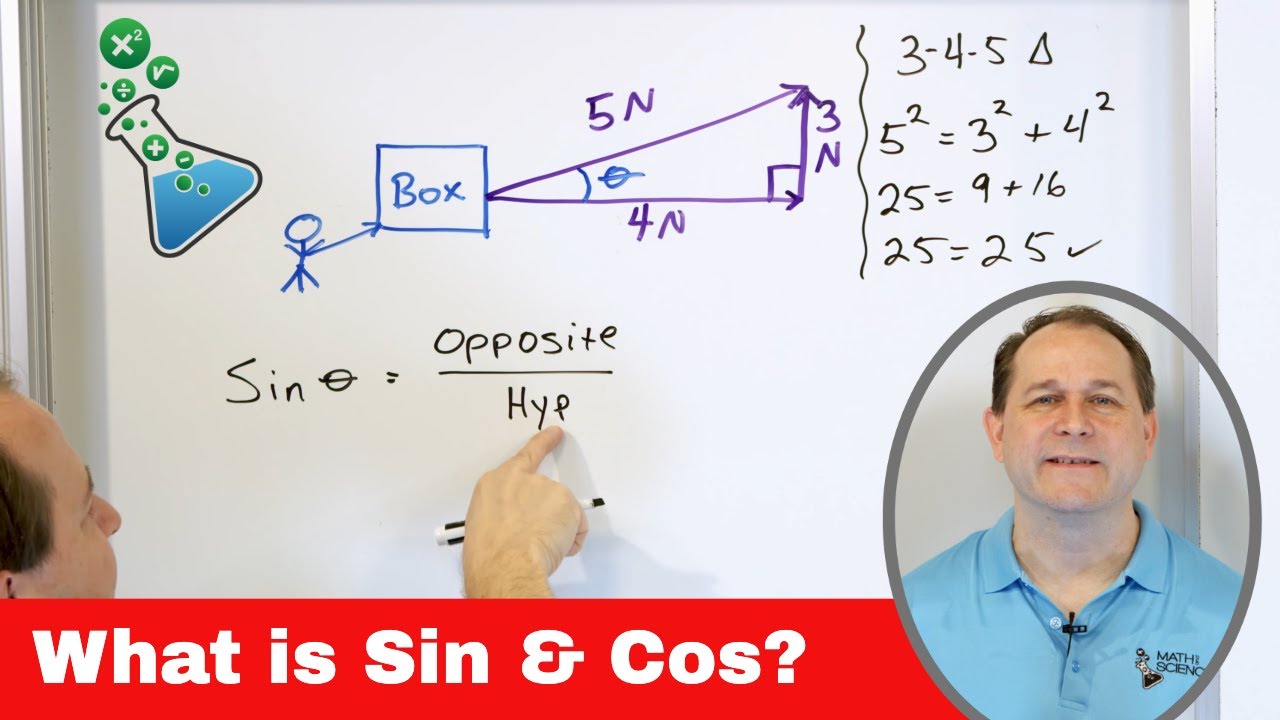
05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?

The Graphs of Sine and Cosine (Precalculus - Trigonometry 11)
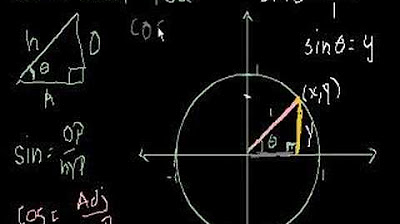
Unit Circle Definition of Trig Functions

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

Calculus 1 Lecture 0.3: Review of Trigonometry and Graphing Trigonometric Functions
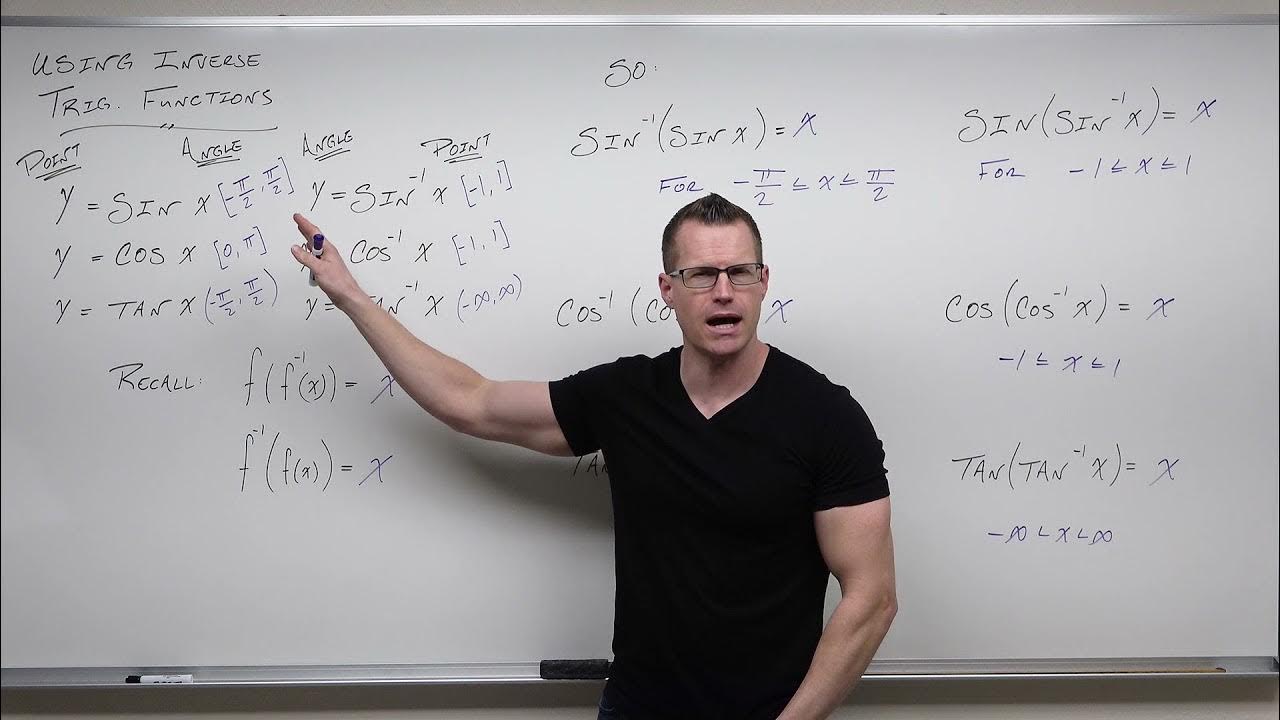
How to Use Inverse Trigonometric Functions (Precalculus - Trigonometry 18)
5.0 / 5 (0 votes)
Thanks for rating: