7.2.5 Determinant of a Square Matrix
TLDRThis video script explains the concept of determinants and their role in finding the inverse of a square matrix, specifically focusing on 2x2 matrices. It outlines the method to calculate the determinant and use it to determine if a matrix has an inverse. The process of finding the inverse of a 2x2 matrix is detailed, with examples provided for matrices with both non-zero and zero determinants. The video also briefly touches on the challenges of calculating determinants and inverses for larger matrices and the use of calculators to assist in these tasks.
Takeaways
- 📚 The determinant of a square matrix is a value that can be calculated from the matrix's elements and is used in various mathematical operations.
- 🔍 For a 2x2 matrix, the determinant is found by multiplying the top left element by the bottom right element and subtracting the product of the top right element and the bottom left element.
- 🔁 Determinants are linked to the inverse of a square matrix; a matrix has an inverse if and only if its determinant is non-zero.
- ❌ A matrix without an inverse is referred to as singular or non-invertible, which is the case when the determinant is zero.
- 🧮 To find the inverse of a 2x2 matrix, one must first check that the determinant is non-zero, then use a specific formula involving swapping the main diagonal elements and changing the signs of the off-diagonal elements.
- 📈 The process of finding the inverse of a matrix becomes more complex for matrices larger than 2x2, often requiring the use of calculators or computational software.
- 🔢 The determinant of a 3x3 matrix can be calculated using a calculator's matrix functions, as demonstrated in the script.
- 🖥️ In the case of matrices with decimal entries, it can be helpful to convert the results into fractions for easier interpretation and manipulation.
- 📊 The video script provides step-by-step instructions on how to calculate the determinant and find the inverse of matrices, emphasizing the importance of these operations in mathematics.
- 🎓 Understanding determinants and matrix inversion is fundamental for studying linear algebra and its applications in various fields.
- 👨🏫 The script serves as an educational resource, guiding viewers through the concepts and procedures of matrix determinants and inverses with clear examples.
Q & A
What is the determinant of a 2x2 square matrix?
-The determinant of a 2x2 square matrix is calculated by multiplying the top left element (a) by the bottom right element (d) and subtracting the product of the top right element (b) and the bottom left element (c).
How is the determinant related to the inverse of a square matrix?
-The determinant is crucial in determining whether a square matrix has an inverse. If the determinant is zero, the matrix does not have an inverse. However, if the determinant is any non-zero number, the matrix does have an inverse.
What happens when the determinant of a matrix is zero?
-If the determinant of a matrix is zero, the matrix does not have an inverse. This is because the inverse of a matrix is directly related to its determinant, and division by zero is undefined in mathematics.
How do you find the inverse of a 2x2 square matrix?
-To find the inverse of a 2x2 square matrix, first ensure that the determinant (ad - bc) is not zero. Then, take the reciprocal of the determinant (1/(ad - bc)), and rearrange the matrix by swapping a with d and changing the signs of b and c. Finally, perform scalar multiplication by multiplying each element in the matrix by the reciprocal of the determinant.
What is the formula for finding the inverse of a 2x2 matrix?
-The formula for the inverse of a 2x2 matrix A with elements a, b, c, and d is given by 1/(ad - bc) times the matrix formed by swapping a with d and changing the signs of b and c: ((1/(ad - bc)) * [(a/d), (-c/b); (-b/a), (c/d)]).
Why is it important to check the determinant before finding the inverse of a matrix?
-Checking the determinant before finding the inverse of a matrix is important because it quickly informs us whether the matrix has an inverse or not. If the determinant is zero, the matrix is singular and does not have an inverse, which means the process of finding the inverse would be futile.
What happens when you try to find the inverse of a matrix with a non-zero determinant?
-When the determinant of a matrix is non-zero, it indicates that the matrix is invertible. You can then proceed to find its inverse using the appropriate formula for the inverse, which involves the determinant and the elements of the original matrix.
How can you use a calculator to find the determinant and inverse of a larger matrix?
-For larger matrices, the process of finding the determinant and inverse can be complex and time-consuming. Calculators with matrix capabilities can be used to input the matrix, calculate the determinant, and then find the inverse if it exists, simplifying the process and reducing the chance of error.
What is the significance of the determinant in linear algebra?
-The determinant is significant in linear algebra as it provides important information about the properties of a matrix, such as whether it is invertible or not. It is also used in solving systems of linear equations, finding the area or volume of geometric shapes, and understanding the behavior of linear transformations.
How does the process of finding the inverse of a matrix differ for larger matrices compared to 2x2 matrices?
-For larger matrices, the process of finding the inverse becomes more complex and typically requires the use of advanced methods such as the Gauss-Jordan elimination, LU decomposition, or the use of a calculator or computer software, as opposed to the straightforward method used for 2x2 matrices.
What are some practical applications of finding the inverse of a matrix?
-The inverse of a matrix is used in various fields such as physics for solving systems of equations that describe multiple variables, in computer graphics for transformations like scaling and rotations, in control theory for system stability analysis, and in finance for portfolio optimization.
Outlines
📚 Introduction to Determinants and Inverse of 2x2 Matrices
This paragraph introduces the concept of determinants, specifically focusing on 2x2 square matrices. It explains the method to calculate the determinant of a 2x2 matrix using the formula of (ad - bc). The significance of the determinant is highlighted in relation to the inverse of a square matrix; if the determinant is zero, the matrix does not have an inverse, but if it is any other number, the matrix does. The process of finding the inverse of a 2x2 matrix using the determinant is also detailed, which involves checking the determinant, rearranging the matrix entries, and performing scalar multiplication with the reciprocal of the determinant. Two examples are provided to illustrate the process, one with a matrix that has an inverse and another that does not due to a determinant of zero.
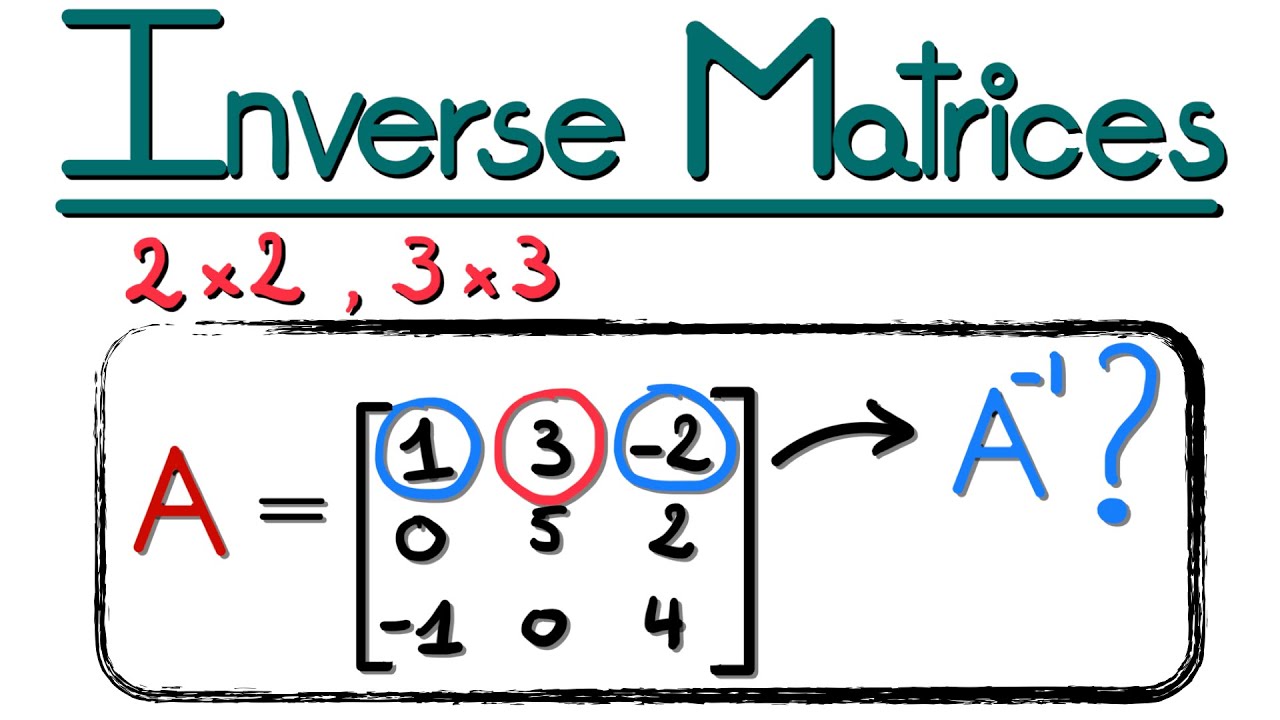
📱 Using a Calculator for Larger Matrices and Finding Inverse
This paragraph discusses the process of finding the determinant and inverse of a 3x3 matrix using a calculator. It emphasizes the complexity of dealing with larger matrices and the utility of calculators in such situations. A 3x3 matrix with specific entries is presented, and the steps to input this matrix into the calculator, calculate its determinant, and subsequently find its inverse are outlined. The calculator results are shown, and the method to convert decimal results into fractions for clarity is briefly explained. The paragraph concludes with the presentation of the final inverse matrix obtained from the calculator.
Mindmap
Keywords
💡determinant
💡square matrix
💡inverse matrix
💡2x2 matrix
💡linear algebra
💡matrix multiplication
💡identity matrix
💡calculus
💡reciprocal
💡scalar multiplication
💡fractions
Highlights
The video begins with an introduction to the concept of determinants, specifically for square matrices.
The determinant of a 2x2 matrix is calculated using the formula ad - bc, where a, b, c, and d are the matrix entries.
Determinants are important because they help determine if a square matrix has an inverse.
A matrix does not have an inverse if its determinant is zero.
If the determinant is non-zero, the matrix has an inverse, and the inverse can be found using the determinant.
To find the inverse of a 2x2 matrix, the entries are rearranged and scalar multiplication is applied using the reciprocal of the determinant.
An example is provided where the matrix [3 1; 4 2] has its determinant calculated as 2, indicating it has an inverse.
The inverse of the matrix [3 1; 4 2] is shown to be [2 -1; -2 1] after applying the method described.
Another matrix example [6 3; 4 2] is given, with its determinant calculated as 0, meaning it does not have an inverse.
The concept of undefined values in mathematics is briefly touched upon, explaining why a matrix with a determinant of 0 cannot have an inverse.
A 3x3 matrix is introduced with entries across the top, middle, and bottom rows.
The process of finding the determinant of the 3x3 matrix using a calculator is demonstrated.
The determinant of the 3x3 matrix is found to be 3, confirming the matrix has an inverse.
The inverse of the 3x3 matrix is calculated using the calculator, showing a matrix with fractional entries.
The video concludes with a reminder of the importance of understanding determinants and inverses in matrix operations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: