6th Grade Math: Finding Surface Area Using Nets

Math with Ms Sun

6 Jun 202017:08

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script introduces the concept of using nets to calculate the surface area of three-dimensional shapes. It explains that a net is a two-dimensional representation of a 3D shape when laid flat. The script covers the nets for common shapes like the rectangular prism, triangular prism, square pyramid, and triangular pyramid, highlighting that opposite faces are identical. It guides viewers through identifying nets corresponding to specific shapes and calculating surface area by summing the areas of the two-dimensional shapes within the net. The video encourages note-taking and active participation, offering step-by-step examples to ensure understanding.

Takeaways

📘 A net is a two-dimensional representation of a three-dimensional shape, showing how it would look if laid flat.
📙 The purpose of using nets is to calculate the surface area of 3D shapes by unwrapping them and identifying the areas of the 2D shapes that make them up.
📕 The video covers the nets for common 3D shapes like the rectangular prism, triangular prism, square pyramid, and triangular pyramid.
📗 The rectangular prism's net has six rectangular faces with opposite faces being identical, reflecting the shape's dimensions.
📒 The triangular prism's net consists of five faces, including two triangles for the bases and three rectangles for the sides, which may or may not be equal depending on the triangle's dimensions.
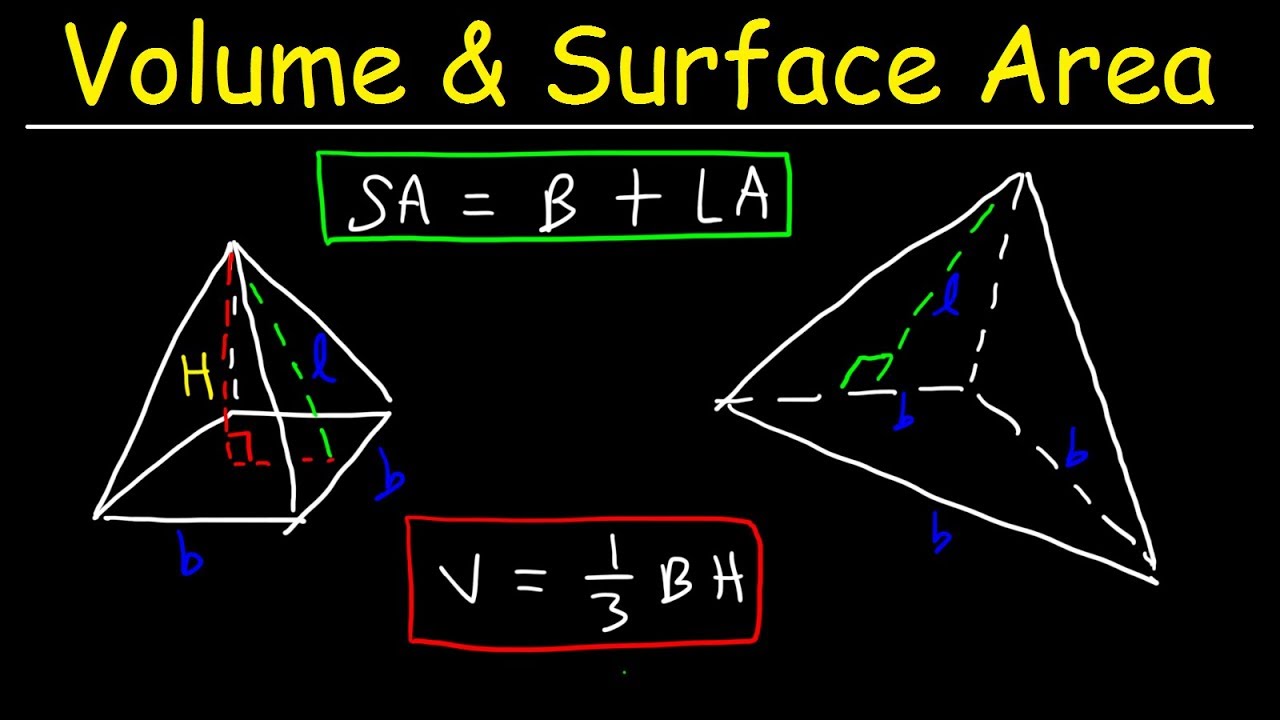
📔 The square pyramid's net features a square base and four equal triangular sides that meet at the apex, indicating its structure.
📓 The triangular pyramid's net has a triangular base and three side triangles, which may or may not be equal, depending on the base triangle's dimensions.
📃 The surface area of a 3D shape is calculated by adding up the areas of all the individual shapes in its net.
📂 The video provides examples of identifying which 3D shape a net corresponds to, such as eliminating options that don't match the expected shape's characteristics.
📁 The process of finding the surface area involves determining the dimensions of the shapes in the net and then calculating the total area by multiplying and adding these dimensions accordingly.
📊 The video script emphasizes the importance of understanding nets and using them as a tool to simplify the calculation of surface area for various 3D shapes.

Q & A

What is a net in the context of three-dimensional shapes?
-A net is a representation of what a three-dimensional shape looks like when it is unwrapped and laid flat. It consists of two-dimensional shapes that, when combined, form the original three-dimensional shape.
Why are nets useful for calculating surface area?
-Nets are useful for calculating surface area because they allow us to see all the individual two-dimensional shapes that make up the three-dimensional shape. By adding up the areas of these shapes, we can determine the total surface area of the object.
What is the surface area of a three-dimensional shape?
-The surface area of a three-dimensional shape is the total outside area that would be covered if you were to wrap the shape with a layer of material, such as paper.
How many rectangular faces does a net of a rectangular prism typically have?
-A net of a rectangular prism typically has six rectangular faces, with opposite faces being identical to each other.
What is the difference between the net of a rectangular prism and a triangular prism?
-A net of a rectangular prism has six rectangular faces, while a net of a triangular prism has five faces, consisting of two equal triangles for the bases and three rectangles for the sides.
How many faces does the net of a square pyramid have?
-The net of a square pyramid has five faces: one square base and four equal triangular side faces that meet at the apex.
What is the base shape of a triangular pyramid?
-The base shape of a triangular pyramid is a triangle, and the net consists of this triangular bottom and three side triangles, making a total of four triangular faces.
How can you determine which net corresponds to a given three-dimensional figure?
-You can determine which net corresponds to a figure by eliminating options that do not match the shape's characteristics, such as the presence of triangles or squares, and then by visualizing the wrapping or unwrapping process of the shape.
How do you calculate the surface area of a cube using its net?
-To calculate the surface area of a cube using its net, you identify that all sides are squares of the same size. Since a cube has six faces, you multiply the area of one square (side length squared) by six to get the total surface area.
What is the formula for calculating the surface area of a rectangular prism given its net?
-To calculate the surface area of a rectangular prism using its net, you find the areas of the different rectangles (length times width for each) and then add them together, remembering that opposite faces are identical and should be multiplied by two before adding.

Outlines

00:00

📐 Introduction to Surface Area Calculation Using Nets

This paragraph introduces the concept of calculating the surface area of three-dimensional shapes using two-dimensional nets. It emphasizes the importance of noting key information and examples, and understanding that a net is the flat representation of a 3D shape. The example of a cube is given to illustrate how its net consists of flat shapes that, when wrapped, form the 3D cube. The goal is to calculate the total outside area of the shape, which is analogous to wrapping paper around the shape. The paragraph also introduces the idea of adding the areas of individual two-dimensional shapes to find the total surface area.

05:02

📏 Understanding Nets for Different 3D Shapes

This section delves into the specifics of nets for various common 3D shapes. The rectangular prism's net is described, highlighting that it consists of six rectangular faces with opposite faces being identical. The triangular prism's net is also discussed, which has five faces including two triangles and three rectangles. The square pyramid's net is characterized by a square base and four equal triangular sides meeting at the apex. Lastly, the triangular pyramid's net is explained, which has a triangular base and three side triangles that may or may not be equal, depending on the base's dimensions. The paragraph reinforces the concept of surface area as the sum of the areas of the shapes within the net.

10:04

🧩 Applying Net Knowledge to Identify 3D Shapes and Calculate Surface Area

The paragraph focuses on applying the knowledge of nets to identify 3D shapes and calculate their surface area. It presents a problem-solving approach where the net of a Rubik's Cube is used to eliminate incorrect options and identify the correct shape. The process of unwrapping and rewrapping the shape in one's mind is suggested as a method to verify the solution. Another example involves calculating the surface area of a cube by adding the areas of its six identical square faces. The paragraph illustrates the mathematical process of multiplying the area of one square by six to find the total surface area, which is 54 square units in the given example.

15:04

📝 Calculating Surface Area of Irregular 3D Shapes

This paragraph extends the concept of surface area calculation to more complex 3D shapes where the faces are not all the same, specifically focusing on the rectangular prism. It guides the viewer through identifying the dimensions of each face of the net and calculating the surface area by adding the areas of the different pairs of faces. The example provided has a rectangular prism with different dimensions for its top and bottom, front and back, and sides. The viewer is shown how to match corresponding sides and multiply their areas by two, then summing these to get the total surface area, which is 52 square units in the example. The paragraph concludes with a reminder to square the units when calculating surface area.

Mindmap

Keywords

💡Surface Area

Surface area refers to the total area of all the surfaces of a three-dimensional object. In the context of the video, it is the cumulative area of the two-dimensional shapes that make up the net of a 3D shape. The script explains how to calculate the surface area by using nets, which are unfolded representations of 3D shapes, to sum the areas of individual shapes to find the total surface area.

💡Nets

Nets are two-dimensional representations of three-dimensional shapes that show how the shape would look if it were laid out flat. They are essential in the video's theme as they provide a visual and mathematical method to calculate surface area. The script uses nets to demonstrate how to unwrap shapes like cubes and rectangular prisms to calculate their surface areas.

💡Three-Dimensional Shapes

Three-dimensional shapes, or 3D shapes, are geometric figures with length, width, and height. The video's main theme revolves around finding the surface area of these shapes using nets. Examples given in the script include cubes, rectangular prisms, triangular prisms, square pyramids, and triangular pyramids.

💡Rectangular Prism

A rectangular prism is a three-dimensional shape with six rectangular faces, where opposite faces are equal in size. The script explains that the net of a rectangular prism consists of six rectangles, with the top and bottom, front and back, and sides being mirror images of each other, making it a key concept in calculating surface area.

💡Triangular Prism

A triangular prism is a polyhedron with two triangular bases and three rectangular sides. The video script describes its net as having five faces, with two equal triangles for the bases and three rectangles for the sides, which may or may not be of equal length depending on the dimensions of the triangular bases.

💡Square Pyramid

A square pyramid is a type of pyramid with a square base and triangular side faces that meet at a common vertex, or apex. The script mentions that the net of a square pyramid includes one square and four congruent triangles, which is crucial for understanding how to calculate its surface area.

💡Triangular Pyramid

A triangular pyramid, also known as a tetrahedron, is a pyramid with a triangular base and three other triangular faces. The video script explains that its net consists of a triangular base and three side triangles, which may or may not be congruent, depending on the base's dimensions.

💡Base Shape

The base shape of a prism or pyramid refers to the polygonal shape that forms the bottom of the three-dimensional figure. In the video, the base shape is important because it dictates the shape and size of the other faces in the net. For instance, a rectangular prism has a rectangular base, and a square pyramid has a square base.

💡Opposite Faces

Opposite faces in the context of the video refer to the pairs of faces in a 3D shape that are mirror images of each other. The script explains that in shapes like the rectangular prism, the top and bottom, front and back, and left and right faces are opposite and identical, which simplifies the calculation of surface area.

💡Calculation

Calculation, in the video's context, involves the mathematical process of determining the surface area of 3D shapes using their nets. The script provides examples of how to calculate surface area by adding the areas of the individual two-dimensional shapes that make up the net, such as multiplying the dimensions of each face and summing them up.

💡Example

Examples in the video are used to illustrate the process of finding surface areas of different 3D shapes using their nets. The script provides step-by-step demonstrations, such as unwrapping a cube and calculating its surface area by adding the areas of its six square faces, which helps viewers understand the concepts being taught.

Highlights

Introduction to finding surface area using nets.

Explanation of what a net is in relation to three-dimensional shapes.

Demonstration of a net for a cube and its unwrapping process.

Importance of understanding nets to calculate the surface area of 3D shapes.

Description of the net for a rectangular prism and its six rectangular faces.

Clarification on how opposite faces of a rectangular prism's net are identical.

Introduction of the triangular prism net with five faces including two triangles and three rectangles.

Details on the net of a square pyramid with one square base and four triangular sides.

Explanation of the triangular pyramid net with four triangular faces and a triangular base.

Emphasis on the method to calculate surface area by adding areas of individual shapes in the net.

Guidance on how to identify which 3D shape a net corresponds to with an example.

Strategy to visualize wrapping up a net to confirm the corresponding 3D shape.

Example problem to find the surface area of a cube using its net.

Explanation of the surface area calculation for a rectangular prism with different face dimensions.

Technique to identify and calculate the surface area for a shape with non-matching faces.

Summary of the process for calculating surface area using nets and adding up areas of shapes.

Invitation for students to ask questions and an indication of future class interaction.

Transcripts

Browse More Related Video

Three-Dimensional Shapes Part 1: Types, Calculating Surface Area

VOLUME OF SOLID FIGURES | GRADE 6

What Is a Prism? | The Dr. Binocs Show | Best Learning Videos For Kids | Peekaboo Kidz

Calculus Chapter 4 Lecture 36 Surface Area

Surface Area of a Pyramid & Volume of Square Pyramids & Triangular Pyramids

Volume