AP Calculus AB Unit 1 Review | Limits and Continuity
TLDRThis video script offers an in-depth exploration of Unit 1 in Calculus AB, focusing on limits and continuity. It explains the concept of limits, including one-sided limits, and how to solve them analytically, especially in cases of indeterminate forms. The script also covers trigonometric limits, the Squeeze theorem, and limits at infinity. Continuity is discussed with examples of discontinuities and how to ensure a function is continuous. The Intermediate Value Theorem is introduced, highlighting its relation to continuity. The video aims to prepare viewers for AP exam questions on these topics.
Takeaways
- 📚 The video covers Unit 1 of Calculus AB, focusing on limits and continuity, which are essential topics for the AP exam.
- 🔍 A limit is defined as the value that a function approaches as the input (x) approaches a certain value. For example, the limit of f(x) as x approaches 1 is 3 for the function y = 3x.
- 📈 Limits can be one-sided, indicated by a plus or minus sign next to the value x approaches, representing the right or left approach respectively.
- 📉 In the case of a piecewise function, if the function does not exist at a certain point but the limit exists, the limit is still defined by the approach of the function's values.
- 🤔 Limits can sometimes be undefined, such as when the left and right limits are different, indicating no single value the function approaches at that point.
- 🧩 Adding or multiplying limits is straightforward and intuitive, as demonstrated with graphical examples.
- 🔢 Analytical solutions for limits involve plugging in values, especially for simple expressions like x squared minus three.
- 💡 Special cases like division by zero require careful handling, where the limit can be infinity or negative infinity depending on the approach.
- 📚 The video also discusses the use of trigonometric identities and special rules for trigonometric limits to solve problems.
- 📉 The Squeeze theorem is introduced as a useful tool for solving limits, especially for trigonometric functions.
- 🌟 Limits to infinity indicate vertical asymptotes, while horizontal asymptotes are approached but never reached, as shown in the graph.
- 📐 Continuity is a concept where a function does not break; it is guaranteed when the limit equals the function's value at a given point.
- 🚫 Discontinuities can occur in three forms: at a point where the limit exists but the function does not, at jumps where the left and right limits differ, and at asymptotes where the function approaches infinity.
- 🔍 The Intermediate Value Theorem (IVT) is related to continuity and states that a continuous function on an interval will take on every value between its endpoints at least once.
Q & A
What is the main topic of Unit 1 in Calculus AB?
-The main topic of Unit 1 in Calculus AB is limits and continuity.
Why are limits important in calculus?
-Limits are important in calculus because they help in understanding the behavior of a function as the input approaches a certain value, and they are a fundamental concept for both multiple-choice questions (MCQs) and free-response questions (FRQs) on the AP exam.
What does the limit of a function represent?
-The limit of a function represents the value that the function approaches as the input variable approaches a certain point.
How can you determine the limit of a function at a certain point if the function is defined piecewise?
-You can determine the limit of a function at a certain point if it's defined piecewise by checking if the function's values converge to a specific number as the input approaches that point, even if the function itself is not defined at that point.
What are one-sided limits and how are they notated?
-One-sided limits are limits that approach a point from either the left or the right side. They are notated with a minus sign (for the left side) or a plus sign (for the right side) next to the value that the input variable approaches.
What does it mean if the limit from the left and the limit from the right are different at a certain point?
-If the limit from the left and the limit from the right are different at a certain point, it means that the overall limit as the input approaches that point does not exist because the function does not approach a single value from both sides.
How can you solve limits analytically for simple expressions?
-You can solve limits analytically for simple expressions by directly substituting the value of the input variable into the function and simplifying the result.
What is the Squeeze Theorem and how is it used in solving limits?
-The Squeeze Theorem states that if a function f(x) is bounded between two other functions g(x) and h(x), and the limits of g(x) and h(x) as x approaches a certain value are the same, then the limit of f(x) is also that value. It is particularly useful for solving trigonometric limits.
How can you determine the limit of a function as the input approaches infinity?
-To determine the limit of a function as the input approaches infinity, you can use rules based on the growth rate of the function's numerator and denominator, such as comparing the leading terms or coefficients, to find if the limit is zero, a finite number, or infinity.
What is continuity and why is it important in calculus?
-Continuity refers to a function that does not have any breaks or jumps in its graph. It is important in calculus because continuous functions have certain properties that allow for the application of calculus operations, such as differentiation and integration.
What are the three types of discontinuities mentioned in the script?
-The three types of discontinuities mentioned are: 1) where a function has a limit but no point at the value of the limit, 2) jumps, where the limit from both sides are different and there is a gap between them, and 3) asymptotes, where the limits go to infinity and never reach each other.
How can you test the continuity of a piecewise function?
-You can test the continuity of a piecewise function by checking if the function's value at a certain point is equal to the limit of the function as the input approaches that point from both sides. If they are equal, the function is continuous at that point; otherwise, it is not.
What is the Intermediate Value Theorem (IVT) and how does it relate to continuity?
-The Intermediate Value Theorem (IVT) states that if a function is continuous on an interval, then it takes on every value between the function's values at the endpoints of the interval at least once. This theorem is related to continuity because it relies on the property that continuous functions do not have gaps in their range.
Outlines
📚 Introduction to Limits and Continuity in Calculus
This paragraph introduces the concept of limits and continuity in calculus, which are key topics in Unit 1 of Calculus AB. The speaker emphasizes the importance of understanding limits for both multiple-choice and free-response questions on the AP exam. Limits are defined as the value that a function approaches as the input approaches a certain point. The concept of one-sided limits is also introduced, denoted by a plus or minus sign, indicating the direction from which the limit is approached. The paragraph covers the intuitive process of adding and multiplying limits and discusses common types of limit problems, including analytical solutions for simple expressions and handling indeterminate forms like 0/0. Trigonometric limits are addressed with the use of trigonometric identities, and special rules for limits involving sine and cosine functions are highlighted. The Squeeze Theorem is introduced as a useful tool for solving trigonometric limits. The paragraph concludes with an explanation of vertical and horizontal asymptotes and how to solve limits involving infinity using growth rate rules.
🔍 Discontinuities and the Intermediate Value Theorem
The second paragraph delves into the topic of discontinuities, which are points where a function is not defined or where the limit exists but is not equal to the function's value at that point. Three types of discontinuities are discussed: a gap, a jump, and asymptotes. The paragraph explains how to test for continuity by comparing the function's value at a point with the limit from both sides. An example is given to illustrate how to find a value that makes a piecewise function continuous by setting the left and right limits equal. The Intermediate Value Theorem (IVT) is introduced as a theorem related to continuity, stating that a continuous function on an interval will take on every value between its endpoints. The speaker provides an example to demonstrate the IVT and concludes by encouraging viewers to review the basic rules covered in the video and to ask questions if anything is unclear, while also promoting the upcoming Unit 2 video.
Mindmap
Keywords
💡Limit
💡Continuity
💡Piecewise Function
💡One-Sided Limit
💡Vertical Asymptote
💡Horizontal Asymptote
💡Squeeze Theorem
💡Discontinuity
💡Intermediate Value Theorem (IVT)
💡Growth Rate
Highlights
Introduction to Unit 1 of Calculus AB focusing on limits and continuity, emphasizing their importance in the AP exam.
Definition of a limit and its significance in the context of a graph approaching a certain value.
Explanation of how to determine the limit of a function as x approaches a specific value.
Illustration of limits in piecewise functions, even when the function is undefined at a certain point.
Introduction to one-sided limits and their notation with plus or minus signs.
Clarification on the non-existence of a limit when left and right limits differ.
Demonstration of adding and multiplying limits with intuitive examples.
Analytical solution of simple limits by direct substitution.
Approach to handle indeterminate forms like 0/0 in limits by simplification.
Use of trigonometric identities to solve trigonometric limits.
Special rules for trigonometric limits involving sine and cosine functions.
Application of the Squeeze theorem for solving limits, especially in trigonometric cases.
Understanding vertical and horizontal asymptotes in the context of limits approaching infinity.
Three simple rules for solving limits as x approaches infinity based on growth rates.
Definition and importance of continuity in functions and its graphical representation.
Identification of three types of discontinuities in functions.
Method to test the continuity of a function by comparing function values and limits.
Strategy to find a value that makes a piecewise function continuous by setting limits equal.
Explanation of the Intermediate Value Theorem and its relation to continuity.
Conclusion summarizing the simplicity of limits and continuity on the AP exam and the importance of remembering basic rules.
Transcripts
Browse More Related Video

One Sided Limits, Graphs, Continuity, Infinity, Absolute Value, Squeeze Thereom - Calculus Review

AP Calculus AB - Chapter 1 Review - Part 2

AP Calculus AB and BC Unit 1 Review [Limits and Continuity]

Calculus 1 Lecture 1.4: Continuity of Functions

Calculus 1 Review - Basic Introduction
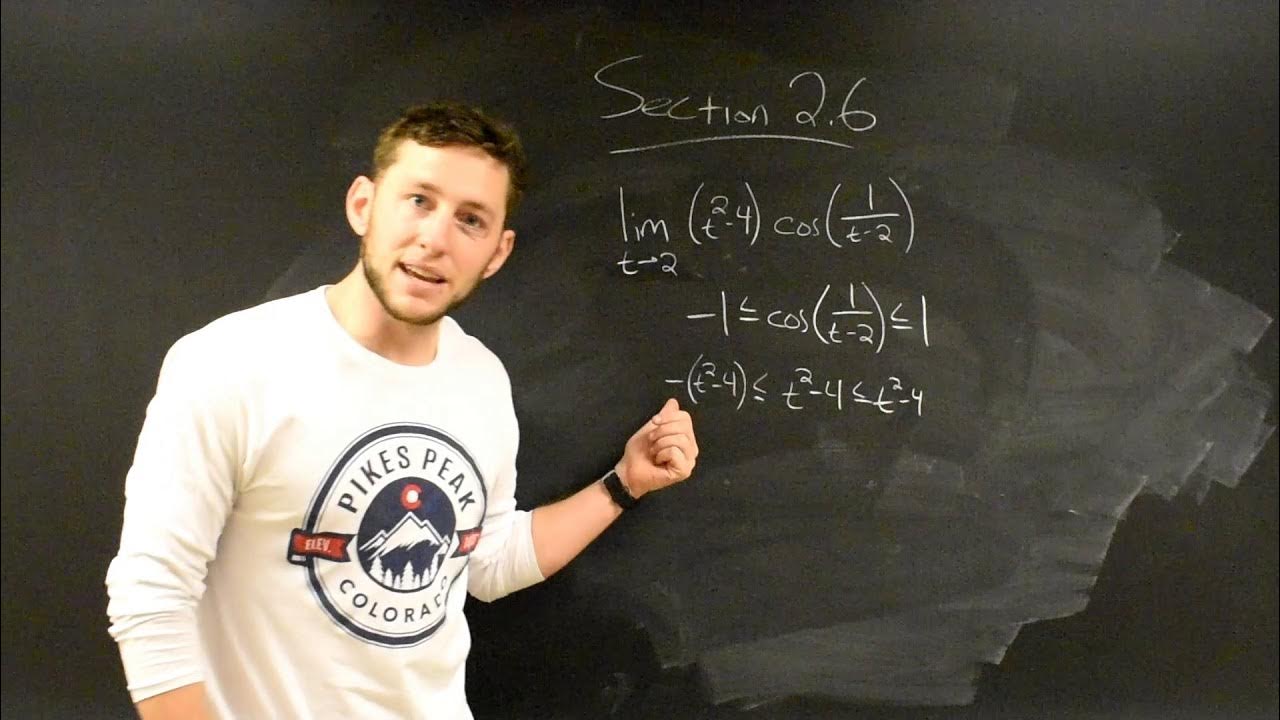
Limits Involving Sine and Cosine & The Squeeze Theorem!
5.0 / 5 (0 votes)
Thanks for rating: