The Einstein Field Equations | Tensor Calc Finale
TLDRThis final episode of the tensor calculus series for physics aims to derive Einstein's field equations in a non-rigorous but insightful manner. The video discusses the criteria these equations must satisfy, such as being a second-rank tensor equation, linear in second derivatives of the metric, and reducing to Poisson's equation in the Newtonian limit. It explores the relationship between the energy-momentum tensor and spacetime geometry, leading to the formulation of Einstein's equations as a balance between the Ricci tensor, scalar, and the metric tensor influenced by mass-energy distribution.
Takeaways
- 📚 The final episode of the tensor calculus series aims to derive Einstein's field equations, providing a conceptual understanding rather than a formal derivation.
- 🔗 The presenter intends to make more videos on tensor calculus in the future, indicating an ongoing interest and commitment to the topic.
- 🔑 The goal of the video is to satisfy the audience's curiosity by arriving at Einstein's field equations through a series of logical arguments.
- 📉 The presenter acknowledges a previous misestimation in covering both Einstein's field equations and the interpretation of curvature tensors in one video, hence splitting the content into separate videos.
- 🔍 The video provides links to previous episodes that explain the Riemann curvature tensor, the Bianchi identities, and the Newtonian limit's relation to the metric tensor, which are foundational for understanding the current topic.
- 🌌 Einstein's field equations are approached by generalizing Poisson's equation to a fully relativistic form, encapsulating mass-energy density in the energy-momentum tensor.
- 📈 The energy-momentum tensor is highlighted as a critical component that encodes information about energy, momentum, pressure, and stress within a system.
- 📉 The video emphasizes the need for the field equations to be linear in second derivatives of the metric tensor, mirroring the properties of Poisson's equation.
- 🔧 The presenter discusses the criteria that the field equations must satisfy, including being a second-rank tensor equation, simple, and reducing to Poisson's equation in the Newtonian limit.
- 🔄 The contracted Bianchi identities are used to derive a relationship between the coefficients of the field equations, narrowing down the possibilities for these coefficients.
- 📝 The derivation of the magnitude of the coefficient 'a' in the field equations is detailed, ultimately concluding that 'a' equals one, aligning with the standard form of Einstein's field equations.
Q & A
What is the main goal of the video?
-The main goal of the video is to arrive at Einstein's field equations through a series of arguments, without a formal derivation, and to provide a satisfying understanding of how these equations are derived.
What is the significance of the energy-momentum tensor in the context of Einstein's field equations?
-The energy-momentum tensor encodes all the information about energy, momentum, pressure, and stress within a system, and it is crucial for fully describing how the geometry of space changes due to the presence of matter.
Why does the video mention the Newtonian limit?
-The Newtonian limit is used to simplify the discussion and to connect the general theory of relativity with classical Newtonian gravity, showing how the Laplacian of the metric tensor in the Newtonian limit is related to mass density.
What is meant by 'keeping it simple stupid' (KISS) in the context of deriving Einstein's field equations?
-The KISS principle is applied to avoid unnecessary complexity in the derivation of Einstein's field equations, focusing on the simplest possible form that still satisfies the required physical conditions.
What does the video suggest as the general form of the Einstein field equations before determining the coefficients?
-The video suggests that the general form of the Einstein field equations could be a linear combination of the Ricci tensor and the Ricci scalar times the metric tensor, with coefficients to be determined.
Why is the divergence of the energy-momentum tensor considered in the derivation?
-The divergence of the energy-momentum tensor is considered because it represents local energy-momentum conservation, which is a fundamental physical principle that the field equations must satisfy.
What role do the contracted Bianchi identities play in the derivation?
-The contracted Bianchi identities provide a relationship between the covariant derivative of the Riemann curvature tensor and the Ricci tensor, which is used to simplify the derivation of the field equations.
What is the significance of the Riemann curvature tensor in the context of the video?
-The Riemann curvature tensor is significant because it represents the intrinsic curvature of spacetime, and it is used to construct the tensors that appear in the Einstein field equations.
How does the video address the issue of the coefficients in the Einstein field equations?
-The video addresses the issue of the coefficients by using the criteria of local energy-momentum conservation and the Newtonian limit to determine the values of these coefficients.
What is the final form of the Einstein field equations presented in the video?
-The final form of the Einstein field equations presented in the video is \( R_{\mu\nu} - \frac{1}{2} R g_{\mu\nu} = 8\pi G T_{\mu\nu} \), where \( R_{\mu\nu} \) is the Ricci tensor, \( R \) is the Ricci scalar, \( g_{\mu\nu} \) is the metric tensor, and \( T_{\mu\nu} \) is the energy-momentum tensor.
Outlines
📚 Final Episode of Tensor Calculus for Physics
This paragraph introduces the final episode of a series on tensor calculus with a focus on physics, based on the book 'Tensor Calculus for Physics.' The speaker hints at the possibility of future videos on the subject due to their love for tensor calculus. The main goal of the episode is to derive Einstein's field equations, not through a formal derivation but through a series of logical arguments. The speaker acknowledges a previous video's optimistic scope and decides to dedicate a separate video to the interpretation of different curvature tensors, including the Riemann curvature tensor, in the future. Key concepts from previous videos, such as the Newtonian limit and the relationship between the metric tensor and gravitational potential, will be referenced to simplify the discussion in this episode.
🔍 Criteria for Einstein's Field Equations
The speaker outlines the criteria that the field equations must satisfy, emphasizing that they should be a second-rank tensor equation, linear in second derivatives of the metric tensor, and simple. The equations should also respect local energy-momentum conservation, meaning the divergence of the energy-momentum tensor should be zero. The paragraph discusses the implications of these criteria, including the reduction of the metric tensor's independent components from ten to six due to symmetry and the requirement for the equations to reduce to Poisson's equation in the Newtonian limit. The speaker also hints at the importance of the Riemann curvature tensor and its relation to the field equations.
🌐 Exploring the Form of g_munu
This paragraph delves into the possible form of g_munu, a component of the field equations, which is expected to be a second-rank tensor. The speaker discusses the need for tensors built from second derivatives of the metric and mentions the Riemann curvature tensor as a candidate due to its unique properties. The paragraph also introduces the Ricci tensor and scalar, as well as the possibility of including terms that vanish in the Newtonian limit, such as a cosmological constant. The speaker concludes that the field equations can be guessed to be a combination of the Ricci tensor and scalar, multiplied by constants, and set equal to the energy-momentum tensor.
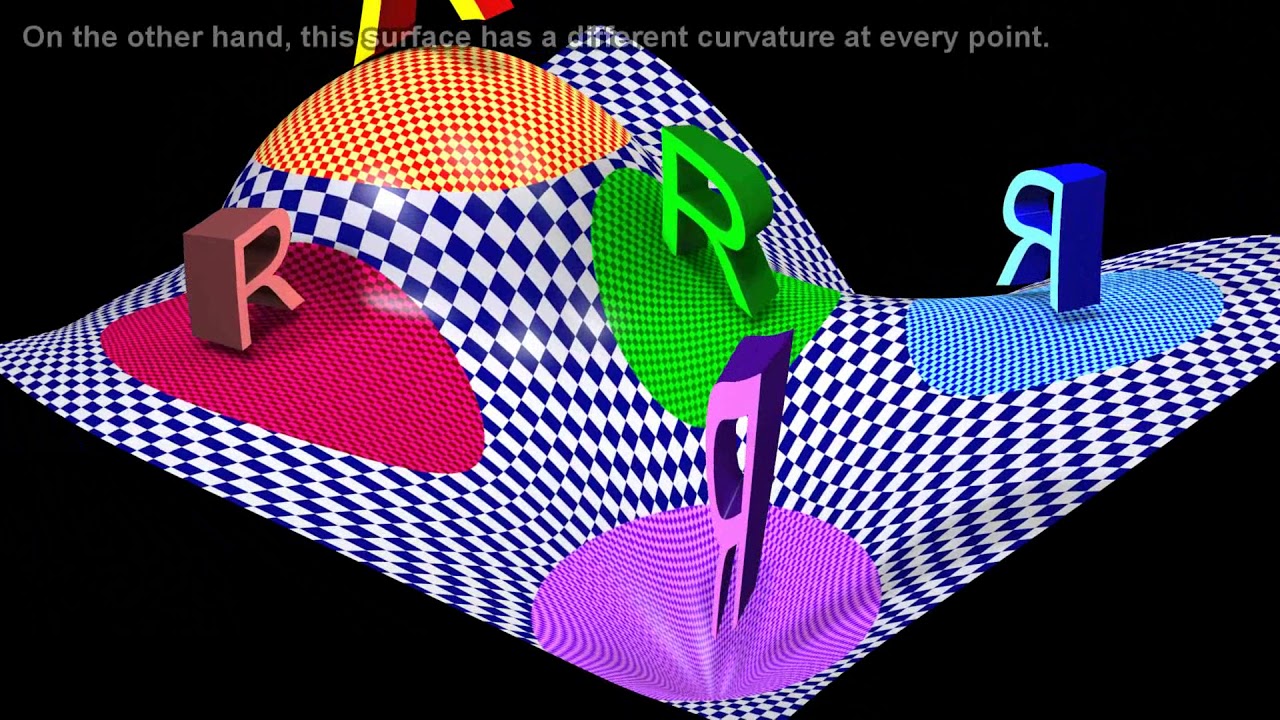
📉 The Significance of the Riemann Curvature Tensor
The speaker expresses a personal dissatisfaction with the fact that the Ricci tensor, rather than the Riemann curvature tensor, explicitly appears in Einstein's field equations. They discuss the properties of the Riemann curvature tensor and its role in describing the intrinsic curvature of subspaces of vectors. The paragraph explores the implications of using the Riemann tensor directly in the field equations and the issues that arise, particularly with vacuum solutions where curvature can still exist even in the absence of mass. The speaker also touches on the redundancy of information in the Riemann tensor compared to the Ricci tensor.
🔧 Determining the Coefficients in Einstein's Field Equations
The paragraph focuses on determining the coefficients in the proposed form of Einstein's field equations using the criterion of local energy momentum tensor conservation. The divergence of both sides of the equation is taken, leading to an expression that must equal zero. By applying the contracted Bianchi identity, the speaker simplifies the equation and finds a relationship between the coefficients. The paragraph concludes with the identification of one unknown variable, 'a', which will be determined through further analysis in the following paragraphs.
📌 Static Weak Field Limit and Riemann Normal Coordinates
The speaker uses the static weak field limit and Riemann normal coordinates to analyze the field equations further. They define the Riemann curvature tensor and its relation to the Ricci tensor in these coordinates, simplifying the expressions by considering the static and weak field conditions. The paragraph discusses the Christoffel symbols and their properties in this limit, leading to an expression for the Ricci tensor in terms of the metric tensor's derivatives. The speaker aims to find the value of 'a' by comparing the field equations to the Laplacian of the gravitational potential in the Newtonian limit.
🧲 Relating the Ricci Tensor to the Laplacian of the Gravitational Potential
This paragraph continues the analysis by relating the zero-zero component of the Ricci tensor to the Laplacian of the gravitational potential in the Newtonian limit. The speaker derives an expression for the Ricci tensor in terms of the metric tensor and its derivatives, leading to a connection with Laplace's equation. The paragraph also discusses the relationship between the Ricci scalar and the zero-zero component of the Ricci tensor, ultimately finding that the Ricci scalar is related to the Laplacian of the gravitational potential as well.
🔄 Determining the Value of Coefficient 'a'
The speaker concludes the determination of the coefficient 'a' by substituting the expressions for the Ricci tensor and scalar into the field equations. They compare the resulting equation to Laplace's equation and find that 'a' must be equal to -1 to satisfy the equation in the Newtonian limit. The paragraph discusses the implications of the sign conventions used throughout the series and how they affect the sign of 'a'. The standard form of Einstein's field equations is presented with 'a' equal to 1, reflecting the most common sign convention.
🎉 Arrival at Einstein's Field Equations
The final paragraph celebrates the arrival at Einstein's field equations after a lengthy series of videos. The speaker humorously relates the significance of the equations to the curvature of space-time caused by massive objects. They reflect on the journey through the series, emphasizing the importance of the physical assumptions made and the challenges of the static weak field limit. The speaker expresses gratitude to the audience for their engagement throughout the series and hints at future videos that may explore solving the field equations for simple cases like the vacuum solution.
👋 Sign Off and Future Engagement
In the closing paragraph, the speaker signs off and invites the audience to engage with future content. They express a desire to see the audience in the next video, indicating an ongoing series or a continuation of the topic. The speaker leaves the audience with an open invitation to continue the exploration of physics and tensor calculus.
Mindmap
Keywords
💡Tensor Calculus
💡Einstein's Field Equations
💡Riemann Curvature Tensor
💡Bianchi Identities
💡Energy-Momentum Tensor
💡Metric Tensor
💡Newtonian Limit
💡Covariant Derivative
💡Christoffel Symbols
💡Ricci Tensor
💡Ricci Scalar
Highlights
Introduction to the final episode of a series on tensor calculus for physics, with a focus on deriving Einstein's field equations.
The goal is to arrive at Einstein's field equations through a series of arguments rather than a formal derivation.
A discussion on the limitations of covering both Einstein's field equations and the interpretations of different curvature tensors in one video.
The importance of the energy-momentum tensor in encoding information about energy, momentum, pressure, and stress.
The generalization of Poisson's equation to a fully relativistic form using a second-rank tensor equation.
Assumption that the equations of motion will be represented by a second-rank tensor equation involving the energy-momentum tensor.
Criteria for the Einstein field equations, including the requirement for them to be a second-rank tensor equation and linear in second derivatives of the metric.
The desire for simplicity in the field equations, avoiding unnecessary complexity.
The necessity for the field equations to satisfy local energy-momentum conservation.
The reduction of the metric tensor's independent components from ten to six due to symmetry and the requirement for divergencelessness.
The requirement for the field equations to reduce to Poisson's equation in the Newtonian limit.
The exploration of tensors built from second derivatives of the metric, such as the Riemann curvature tensor.
The uniqueness of the Riemann curvature tensor and its role in constructing the field equations.
The decision to use the Ricci tensor and scalar, derived from the Riemann curvature tensor, as components of the field equations.
The process of finding the coefficients of the field equations by considering local energy-momentum tensor conservation.
The use of contracted Bianchi identities to simplify the derivation of the field equations.
The derivation of the Einstein field equations in the form Rμν - (1/2)Rgμν = 8πGTμν, with the coefficient 'a' determined to be 1.
Reflection on the significance of the derived field equations and their implications for understanding how matter curves spacetime.
The presenter's intention to potentially explore solutions to the field equations in future videos.
Acknowledgment of the audience's engagement throughout the lecture series and an invitation for feedback.
Transcripts
Browse More Related Video

Relating Metric Tensor to Gravity | Tensor Calculus Ep. 16

General Relativity Lecture 9

Einstein Field Equations - for beginners!

Tensor Calculus 26 - Ricci Tensor/Scalar Properties

Tensor Calculus For Physics Majors 006 | The Metric Tensor pt. 1
Einstein's Field Equations of General Relativity Explained
5.0 / 5 (0 votes)
Thanks for rating: