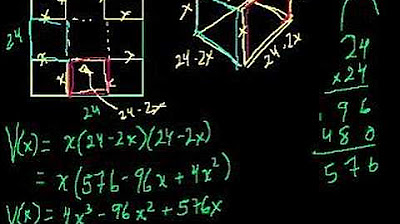Optimisation Grade 12

Kevinmathscience
20 May 202105:21
EducationalLearning
32 Likes 10 Comments

TLDRThe video script guides students through a geometric problem involving maximizing the volume of an open-top box made from a square piece of paper by cutting and folding. The original dimensions of the paper are given, and students are instructed to visualize the process of creating the box by folding corners up, resulting in a box with a volume formula dependent on the variable x. The script then applies calculus to find the maximum volume by setting the first derivative of the volume equation to zero and solving for x. Two solutions are obtained, but only x = 10 yields a realistic maximum volume, as x = 33.33 results in a negative volume, which is physically impossible.

Takeaways
  • 📚 The speaker is addressing a common issue where students struggle to visualize the problem at hand.
  • 📝 The exercise involves imagining a piece of paper and cutting out squares from its corners to form a 3D shape without a lid.
  • 📐 The speaker guides the audience to visualize the process of bending the edges of the paper upwards to create the shape of a box.
  • 📉 The objective is to find the value of 'x' that maximizes the volume of the box, indicating the use of calculus to solve the problem.
  • 🔢 The dimensions of the box are derived from the original paper size, with the length being 80 - 2x, the breadth 50 - 2x, and the height x.
  • 📈 The volume of the box is expressed as a function of 'x', which is simplified to a cubic equation in 'x'.
  • 🧠 The speaker explains that to find the maximum volume, one must take the first derivative of the volume equation and set it to zero.
  • ✏️ The derivative of the volume equation is solved using the quadratic formula, yielding two potential solutions for 'x'.
  • 🔍 The speaker emphasizes the importance of interpreting mathematical answers in a real-world context, ruling out the negative volume solution.
  • 📊 To determine the maximum volume, the speaker suggests plugging the two solutions for 'x' back into the volume equation and comparing the results.
  • 🏁 The conclusion is that when x is 10, the volume of the box is at its maximum, which is 18,000 cubic units.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is to guide students through the process of visualizing a geometric problem involving a piece of paper being transformed into a box, and then using calculus to find the maximum volume of the box.

  • Why is it important to visualize the problem correctly?

    -Visualizing the problem correctly is crucial because it helps students understand what the question is asking and sets the foundation for solving the problem accurately.

  • What shape is initially described in the transcript?

    -The initial shape described is a piece of paper, which is then manipulated to form a box without a lid.

  • How is the piece of paper transformed into the box?

    -The transformation involves cutting out squares from the corners of the paper and then bending the edges upwards to form the sides of the box.

  • What mathematical concept is used to find the maximum volume of the box?

    -The mathematical concept used to find the maximum volume is calculus, specifically by taking the first derivative of the volume equation and setting it to zero to find critical points.

  • What are the dimensions of the original piece of paper?

    -The original dimensions of the piece of paper are 80 units in length and 50 units in breadth.

  • How does the length of the box change after cutting out the squares?

    -The length of the box becomes 80 minus 2x, where x is the length of the side of the square cut out from the corners.

  • What is the formula used to calculate the volume of the box?

    -The formula used to calculate the volume of the box is length times breadth times height, which becomes (80 - 2x) * (50 - 2x) * x after substituting the dimensions.

  • What is the simplified form of the volume equation after multiplying out the brackets?

    -The simplified form of the volume equation is -260x^2 + 4000x.

  • How many critical points are found when setting the first derivative equal to zero?

    -Two critical points are found: x equals 10 and x equals approximately 33.3.

  • Which value of x gives the maximum volume of the box?

    -When x is 10, the volume of the box is at its maximum, which is 18,000 cubic units.

  • Why is the solution of x approximately 33.3 not applicable in this context?

    -The solution of x approximately 33.3 is not applicable because it results in a negative volume, which doesn't make sense in real-life scenarios where volume cannot be negative.

Outlines
00:00
📏 Visualizing the Geometry of a Box Problem

The speaker introduces a geometric problem involving a piece of paper that is transformed into a box. The audience is guided to visualize cutting squares from the corners of the paper and folding the sides up to form a box without a lid. The focus is on understanding the shape and dimensions of the box, which will be essential for solving the problem. The length, breadth, and height of the box are described in terms of the variable x, which represents the size of the squares cut from the paper.

05:00
📐 Applying Calculus to Maximize Box Volume

The speaker proceeds to explain how to calculate the volume of the box using the dimensions derived from the previous visualization. The volume is expressed as a function of x, and the formula is simplified to a cubic equation. To find the maximum volume, the speaker uses calculus, specifically the first derivative, and sets it equal to zero to find critical points. The quadratic formula is applied to solve for x, yielding two potential solutions. The speaker emphasizes the importance of interpreting these mathematical results in the context of the real-world problem, ultimately determining that x equals 10 provides the maximum volume for the box, while the other solution is discarded as it results in a negative volume, which is not physically meaningful.

Mindmap
Keywords
💡Visualization
Visualization refers to the ability to form a mental image or picture of something that is not present or cannot be seen. In the video's context, it is essential for students to visualize the geometric shapes and transformations described to understand the problem-solving process. For example, the script asks students to imagine a piece of paper and then visualize cutting out squares from the corners to form a 3D shape.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. In the video, calculus is used to find the maximum volume of the 3D shape created by the paper folding process. The script mentions using calculus to determine the value of 'x' that maximizes the volume, indicating the application of derivatives to find the critical points of the volume function.
💡Volume
Volume is the measure of the amount of space occupied by a three-dimensional object. The video's main theme revolves around calculating the volume of a box formed by folding a piece of paper. The script explains how to calculate the volume by multiplying length, breadth, and height, and then uses this formula to derive an equation for the volume in terms of 'x'.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. The script uses the first derivative of the volume function to find the points where the volume could be at a maximum or minimum. The first derivative is set to zero to find critical points, which are then analyzed to determine the maximum volume.
💡Quadratic Formula
The quadratic formula is a method used to solve quadratic equations of the form ax^2 + bx + c = 0. In the script, the quadratic formula is applied to the first derivative of the volume function to find the values of 'x' that make the derivative zero, which are potential candidates for maximum or minimum volume.
💡Critical Points
Critical points are the points on a graph where the derivative is zero or undefined, indicating potential maxima or minima. The script identifies critical points by setting the first derivative equal to zero and solving for 'x', which are then evaluated to find the maximum volume of the box.
💡Maximum Volume
Maximum volume refers to the largest possible volume that an object can occupy under given constraints. The video's objective is to find the dimensions that result in the maximum volume of the paper box. The script guides the audience through the process of using calculus to determine the value of 'x' that maximizes the volume function.
💡First Derivative Test
The first derivative test is a method used to determine the local maxima and minima of a function by analyzing the sign of the first derivative around critical points. The script uses this test to find the critical points and then evaluates them to identify the maximum volume of the box.
💡Geometric Transformation
Geometric transformation involves changing the shape, size, or position of a geometric figure without altering its intrinsic properties. In the video, the script describes a series of transformations applied to a piece of paper to create a 3D box, which is a key part of visualizing and solving the problem.
💡Real-life Application
Real-life application refers to the practical use of theoretical concepts in everyday situations. The script emphasizes the importance of interpreting mathematical results in a way that makes sense in real-life contexts, such as dismissing a negative volume as an impossible outcome when considering the physical constraints of the problem.
💡Interpretation
Interpretation in mathematics involves understanding and making sense of mathematical results within a given context. The script highlights the need for human judgment to interpret mathematical solutions, such as recognizing that a negative volume is not applicable to the physical world.
Highlights

The importance of visualizing the problem before attempting to solve it.

Using a piece of paper to demonstrate the concept of creating a box with maximum volume.

Cutting out square corners from the paper to form the base of the box.

Bending the sides of the paper upwards to create the box shape.

The box is visualized without a lid for simplicity.

Determining the value of x to maximize the volume of the box using calculus.

Calculating the length, breadth, and height of the box based on the value of x.

Formulating the volume equation as length times breadth times height.

Expanding and simplifying the volume equation to prepare for differentiation.

Taking the first derivative of the volume equation to find critical points.

Setting the first derivative equal to zero to solve for x.

Using the quadratic formula to find the possible values of x.

Interpreting the mathematical solutions to find the one that makes sense in the context of the problem.

Evaluating which value of x results in a maximum volume for the box.

Rejecting the negative volume solution as it does not make sense in real-life applications.

The conclusion that x equals 10 gives the maximum volume for the box.

Transcripts

Browse More Related Video

Optimization with Calculus 2

Optimisation [IB Maths AI SL/HL]

Optimisation Grade 12: Maximum Volume Box

Ex: Optimizing the Volume of a Box With Fixed Surface Area

Optimisation Grade 12: Maximum Surface Area Box

Maximization Word Problem #2!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusMathematicsVolume MaximizationVisualizationStep-by-StepProblem SolvingEducationalTutorialMath StudentsGeometry