AP Physics B Kinematics Presentation General Problems #12
TLDRThis script explains the physics of a projectile launched from a 95-meter cliff with an initial velocity of 15 m/s at a 37-degree angle. It calculates the maximum height reached at 141 meters, the total time in the air as 8.4 seconds, and the horizontal distance covered at 335 meters. The script also determines the velocity of the projectile just before impact at the cliff's base, which is 66 m/s, using fundamental projectile motion equations and the Pythagorean theorem.
Takeaways
- 🎯 The initial speed of the projectile is 50 meters per second at an angle of 37 degrees above the horizontal.
- 🧮 The vertical acceleration is -9.8 meters per second squared and the horizontal acceleration is 0 meters per second squared.
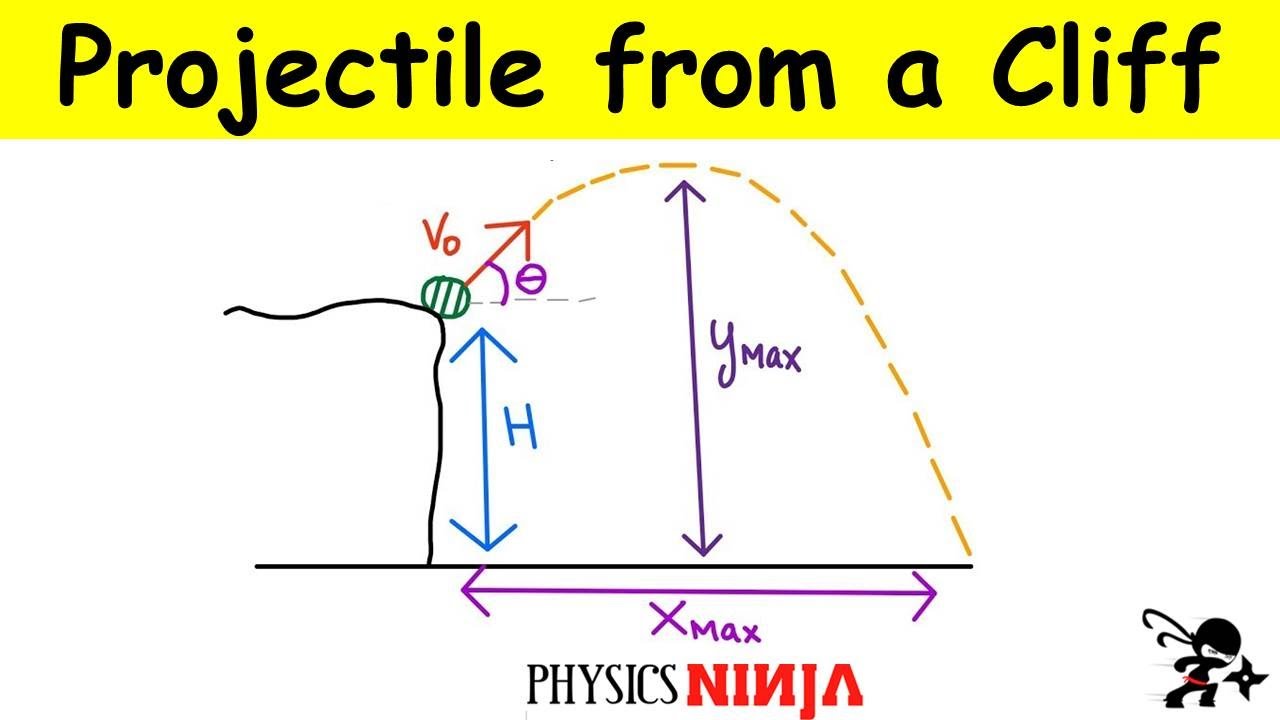
- ⛰️ The cliff from which the projectile is fired is 95 meters high.
- 🚀 The maximum height reached by the projectile above the ground is calculated to be 141 meters.
- ⏱️ The total time the projectile is in the air is determined to be 8.4 seconds.
- 📏 The maximum horizontal distance covered by the projectile is 335 meters.
- 📐 To find the velocity just before the projectile hits the ground, the vertical and horizontal components of the velocity are calculated.
- 🔽 The vertical component of the velocity just before impact is -52 meters per second.
- ➡️ The horizontal component of the velocity just before impact is 40 meters per second.
- 📊 The resultant velocity of the projectile just before it hits the ground is 66 meters per second.
Q & A
What is the initial speed of the projectile fired from the cliff?
-The initial speed of the projectile is 15 meters per second.
What is the height of the cliff from which the projectile is launched?
-The cliff is 95 meters high.
What is the angle at which the projectile is launched above the horizontal?
-The projectile is launched at an angle of 37 degrees above the horizontal.
What is the formula used to calculate the maximum height reached by the projectile?
-The formula used is \( y_{\text{apex}}^2 = v_{0y}^2 + 2a_{y}\Delta y \).
What is the vertical acceleration acting on the projectile?
-The vertical acceleration is \( g \), which is -9.8 meters per second squared.
How is the maximum height calculated in the script?
-The maximum height is calculated by rearranging the formula to solve for \( y \) and plugging in the given values.
What is the total time the projectile spends in the air before hitting the ground?
-The total time in the air is 8.4 seconds.
What formula is used to determine the time of flight of the projectile?
-The formula used is \( y = y_0 + v_{0y}T + \frac{1}{2}a_yT^2 \), which is rearranged to form a quadratic equation in terms of \( T \).
What is the maximum horizontal distance covered by the projectile?
-The maximum horizontal distance covered is 335 meters.
How is the horizontal distance calculated?
-The horizontal distance is calculated using the formula \( x = x_0 + v_{0x}T \), with \( x_0 = 0 \) and \( a_x = 0 \).
What is the velocity of the projectile just before it hits the bottom of the cliff?
-The velocity of the projectile just before impact is 66 meters per second.
How is the final velocity of the projectile calculated?
-The final velocity is calculated using the Pythagorean theorem, by finding the square root of the sum of the squares of the horizontal and vertical velocity components.
Outlines
🚀 Projectile Motion Analysis
This paragraph discusses the physics of projectile motion, specifically the calculation of the maximum height reached by a projectile. The given scenario involves a projectile launched from a 95-meter cliff with an initial velocity of 15 m/s at a 37-degree angle. The vertical acceleration due to gravity is -9.8 m/s², and the horizontal acceleration is 0. The initial vertical position is 95 meters, and the horizontal position is assumed to be zero. The paragraph explains the use of the formula for the maximum height (y_apex) in projectile motion, which is derived from the kinematic equations, to find that the projectile reaches a height of 141 meters above the ground.
⏱ Calculating Time of Flight
The second paragraph focuses on determining the total time the projectile spends in the air. It starts by setting up the kinematic equation for vertical motion, considering the initial vertical position (95 meters) and the final vertical position (0 meters at ground level). The paragraph then transforms the equation into a quadratic form to solve for the time of flight (T). Using the quadratic formula, the paragraph calculates the time it takes for the projectile to reach the bottom of the cliff, which is found to be 8.4 seconds, disregarding the negative solution as it is not physically meaningful in this context.
📏 Determining Horizontal Range
In this paragraph, the calculation of the horizontal distance covered by the projectile is presented. By using the horizontal component of the initial velocity and the time of flight determined in the previous paragraph, the horizontal range is calculated. Since there is no horizontal acceleration, the horizontal motion is uniform, and the range is found by multiplying the horizontal component of the initial velocity (50 m/s at a 37-degree angle) by the total time of flight (8.4 seconds), resulting in a horizontal distance of 335 meters.
🌪 Final Velocity Components
The final paragraph addresses the determination of the projectile's velocity just before it hits the bottom of the cliff. It breaks down the velocity into its vertical (V_y) and horizontal (V_x) components. The vertical component is calculated using the initial vertical velocity, the acceleration due to gravity, and the time of flight, resulting in a final vertical velocity of -52 m/s. The horizontal component remains constant due to zero horizontal acceleration, resulting in a horizontal velocity of 40 m/s. The paragraph then combines these components to find the resultant velocity at impact using the Pythagorean theorem, yielding a velocity of 66 m/s.
Mindmap
Keywords
💡Projectile
💡Initial Velocity
💡Angle of Projection
💡Vertical Acceleration
💡Horizontal Acceleration
💡Cliff Height
💡Apex
💡Trajectory
💡Time of Flight
💡Horizontal Distance
💡Resultant Velocity
Highlights
A projectile is launched from a 95-meter high cliff with an initial speed of 15 meters per second at a 37-degree angle.
The initial velocity is given as 50 meters per second, which is a typographical error in the transcript.
The vertical acceleration due to gravity is -9.8 m/s², and the horizontal acceleration is 0 m/s².
The projectile's maximum height is calculated using the formula for vertical displacement in projectile motion.
The highest point reached by the projectile is 141 meters above the ground.
The total time in the air is determined by solving a quadratic equation for time.
The time to reach the bottom of the cliff is calculated to be 8.4 seconds.
The horizontal distance covered by the projectile is found using the horizontal velocity and time in the air.
The projectile covers a horizontal distance of 335 meters before hitting the ground.
The velocity components just before impact are calculated separately for the horizontal and vertical directions.
The vertical component of the velocity at impact is found to be -52 m/s, indicating a downward direction.
The horizontal component of the velocity remains constant at 40 m/s due to no horizontal acceleration.
The resultant velocity at the bottom of the cliff is calculated using the Pythagorean theorem.
The projectile's velocity just before impact is 66 m/s.
The problem-solving approach demonstrates the application of projectile motion equations in real-world scenarios.
The importance of accurate initial conditions for the correct calculation of projectile motion is highlighted.
The method illustrates the step-by-step process of solving for various aspects of projectile motion.
The transcript provides a clear example of how to apply physics formulas to calculate projectile motion parameters.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: