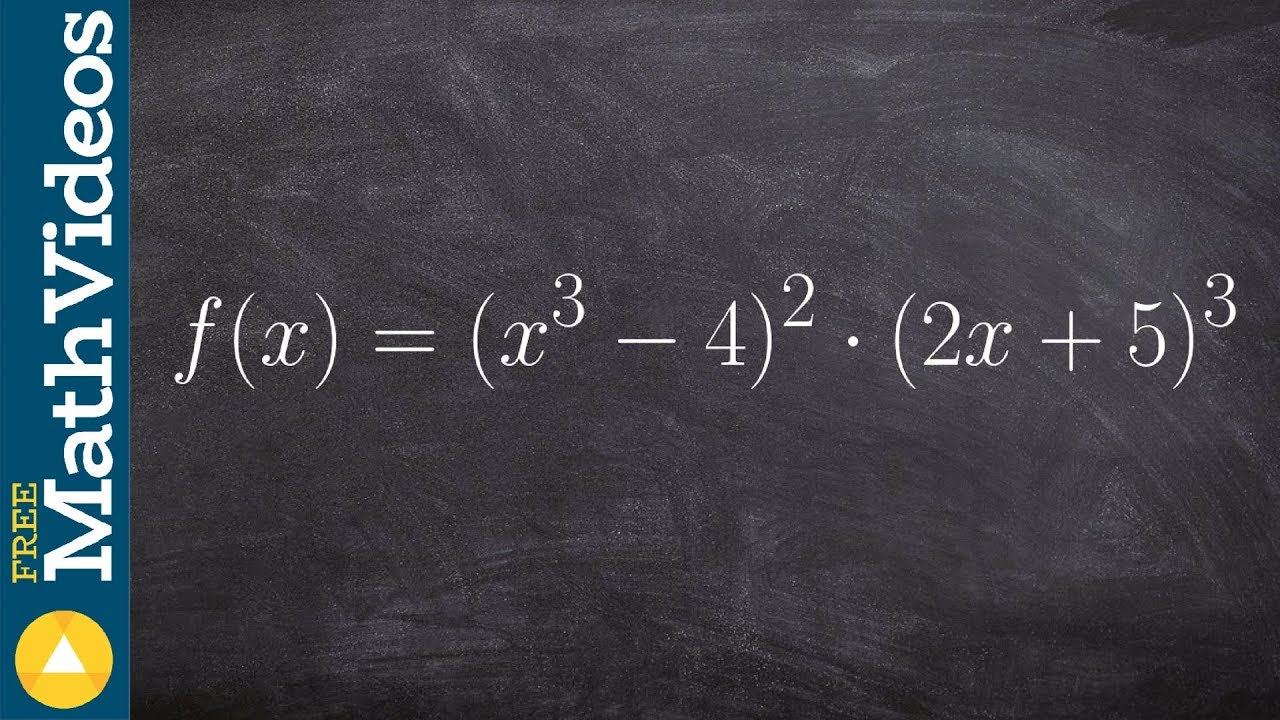First Principles exam Questions

Kevinmathscience

27 Apr 202304:38

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial explains how to determine the first derivative of a function using first principles. The instructor breaks down the process step by step, starting with the fundamental formula for the derivative. By working through an example where the function is negative x squared, the tutorial highlights common pitfalls, especially regarding signs and algebraic manipulation. The video emphasizes the importance of correctly applying the formula and simplifying expressions to arrive at the correct derivative, which in this case, is -2x.

Takeaways

📜 The first derivative can be determined using the first principles formula.
📈 The formula is the limit as H approaches zero of [f(x + h) - f(x)] / H.
🤔 Many learners struggle with this formula, but it's manageable with proper steps.
🔄 To apply the formula, replace x with x + h in the function f(x).
🧮 Example: For f(x) = -x², f(x + h) becomes -[(x + h)²].
➕ Be mindful of signs; they can easily cause mistakes, especially negatives.
🧩 Simplify the expression step by step, combining like terms and distributing negatives.
🚫 Terms without H should cancel out after simplification.
💡 Factor out H from the remaining terms, allowing you to cancel it with the denominator.
✔️ Finally, let H approach zero, simplifying the expression to find the derivative.

Q & A

What is the first principle formula for finding the derivative?
-The first principle formula for finding the derivative is the limit as H approaches zero of the expression [f(x + h) - f(x)] / h.
Why do some learners struggle with using the first principle formula?
-Learners often struggle with the first principle formula because it involves substituting variables and simplifying expressions, which can be confusing, especially with negatives and complex expressions.
How do you substitute f(x) in the first principle formula?
-To substitute f(x) in the first principle formula, you replace all instances of 'x' in the function with 'x + h' for f(x + h).
What should you do with the 'minus' sign in the first principle formula?
-You should carefully apply the 'minus' sign when subtracting f(x) from f(x + h) to avoid mistakes, especially when dealing with negative terms.
What happens to the terms without 'h' after expanding and simplifying?
-Terms without 'h' should cancel out after expanding and simplifying the expression. If they don't, it indicates a mistake in the process.
Why is it important to cancel out the 'h' in the denominator?
-It's important to cancel out the 'h' in the denominator because if 'h' were to go to zero while in the denominator, it would create an undefined expression. Canceling allows you to safely take the limit.
What is the final step in finding the derivative using first principles?
-The final step is to let 'h' approach zero after canceling out 'h' in the denominator, which gives the derivative. In this case, the final answer is -2x.
Why do you need to expand the expression in brackets carefully?
-Carefully expanding the expression in brackets is crucial because mistakes here can lead to incorrect simplifications and a wrong final answer.
What is the purpose of finding the derivative using first principles in this problem?
-The purpose is to demonstrate the understanding of the derivative concept through a step-by-step process, which is especially important when explicitly required in exams or assignments.
How do you handle the negative sign when expanding (x + h)²?
-When expanding (x + h)², you should distribute the negative sign across all terms after the expansion to ensure the correct signs in your expression.

Outlines

00:00

📐 Understanding the First Derivative Using First Principles

This paragraph introduces the concept of determining the first derivative using first principles. The speaker begins by recalling the first principles formula, which involves calculating the limit as H approaches zero of the function f(x+h) minus f(x) divided by H. The speaker acknowledges that many learners struggle with this concept and aims to simplify it. A step-by-step approach is presented, emphasizing the substitution of variables and simplifying the formula to make it more accessible.

📝 Substituting Values into the Formula

The speaker explains how to substitute values into the first principles formula. By replacing x with specific values, such as f(1) or f(2), learners can understand the process. The concept of substituting x with (x + h) is also introduced, showing how to modify the function accordingly. This process is crucial for applying the first principles formula correctly.

🔄 Simplifying the Expression

The paragraph focuses on simplifying the expression derived from the first principles formula. The speaker emphasizes the importance of writing the limit as H approaches zero throughout the process. The steps involve expanding and simplifying the expression, dealing with negatives, and combining like terms. The speaker also provides tips for avoiding common mistakes, particularly when handling negative signs in the equation.

➖ Canceling Out Terms and Finalizing the Result

In this section, the speaker explains how to cancel out terms in the expression to reach the final result. The key idea is that after simplification, all terms without an H should cancel out. The remaining terms are then factored and simplified further until the final derivative is obtained. The speaker emphasizes the importance of canceling the H at the bottom of the expression before letting H approach zero, which leads to the final answer of -2x.

🎓 Conclusion: Applying First Principles for Full Marks

The final paragraph wraps up the explanation by highlighting the importance of following the first principles method, especially when required by the question. While the final result of -2x can be obtained using other methods, the speaker underscores that using the first principles approach is essential for earning full marks in an exam setting. The detailed process is necessary to demonstrate understanding and to meet the question's requirements.

Mindmap

Keywords

💡First Derivative

The first derivative of a function represents the rate at which the function's value changes as its input changes. In the context of the video, it is calculated using first principles, which involves finding the limit as H approaches zero. The first derivative is central to understanding how a function behaves and is fundamental in calculus, particularly in determining the slope of a tangent to the curve at any point.

💡First Principles

First principles refer to the basic method of deriving the first derivative of a function by applying the definition of a derivative. In the video, the process involves using the formula limit as H approaches zero of [f(x+h) - f(x)] / H. This method is essential for understanding the foundational concept of derivatives before using shortcuts like the power rule.

💡Limit

A limit describes the value that a function approaches as the input approaches a certain point. In the video, the limit is taken as H approaches zero to calculate the first derivative. Understanding limits is crucial because it helps in defining derivatives and continuity, which are key concepts in calculus.

💡H (in the context of calculus)

In the context of calculus, H represents a small increment in the input value of a function. As H approaches zero, it helps to determine the exact rate of change (derivative) of the function. The video repeatedly emphasizes how H is used in the first principles method to calculate the derivative.

💡Function (f(x))

A function f(x) is a mathematical relationship where each input (x) has a corresponding output. In the video, the function being differentiated is f(x) = -x². Understanding the behavior of functions is crucial for applying calculus concepts, as derivatives describe how these functions change.

💡Substitution

Substitution refers to replacing a variable in a function with a given value or expression. In the video, substitution is used when f(x+h) is computed by replacing x in the function with (x+h). This step is fundamental in applying first principles to find the derivative.

💡Simplification

Simplification involves reducing an expression to its simplest form. In the video, after applying the first principles formula, various algebraic steps are taken to simplify the expression, such as expanding brackets and canceling terms, leading to the final derivative result.

💡Negative Sign Handling

Negative sign handling refers to correctly managing negative signs during calculations. The video highlights how mistakes can occur if negatives are not carefully handled, especially during the simplification process. Proper handling ensures that the final answer is correct.

💡Common Factor

A common factor is a term that is common in all parts of an expression and can be factored out. In the video, H is factored out from the numerator of the expression, which simplifies the process of finding the derivative by canceling it with the H in the denominator.

💡Final Answer

The final answer refers to the result obtained after all the calculations are completed. In the context of the video, the final derivative of the function f(x) = -x² using first principles is -2x. The video emphasizes the importance of following through each step carefully to arrive at this correct answer.

Highlights

Explanation of the first derivative using first principles.

Introduction to the first principle formula for derivatives.

Clarification on how to substitute values into the function f(x).

Example using f(x) = -x^2 to demonstrate substitution.

Step-by-step guide on substituting x+h into the function.

Instruction on writing the limit expression throughout the process.

Simplification of the expression after substitution.

Warning about potential mistakes when dealing with negative signs.

Multiplication of terms within the brackets and simplification.

Key insight: Everything that doesn't have an h should cancel out.

Factoring out h as a common factor from the expression.

Explanation of why you can let h approach zero in the final steps.

Final simplification to reach the derivative result of -2x.

Comparison to the first method of taking the derivative directly.

Emphasis on the importance of using the first principles method for full marks.

Transcripts

Browse More Related Video

First principles grade 12: Practice

Definition of the Derivative

First Principles Calculus Grade 12 | With Fraction

How to take the derivative with chain rule inside product rule

How To Find The Equation of the Normal Line