How To Find The Equation of the Normal Line

The Organic Chemistry Tutor
30 Dec 201910:25
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial explains the process of finding the equation of a normal line to a given curve at a specific point. It begins with a clear introduction to the concept, using the curve y=x^2 as an example. The video demonstrates how to calculate the slope of the tangent line by taking the first derivative of the function, and then finding the negative reciprocal to determine the slope of the normal line. The method is applied to two examples, showing the step-by-step process of finding the y-coordinate of the point of intersection, calculating the slopes, and finally using the point-slope formula to derive the equation of the normal line. The video is a comprehensive guide for anyone looking to understand the mathematical principles behind finding normal lines to curves.

Takeaways
  • 📚 The video discusses the method for finding the equation of a normal line to a curve at a given point.
  • 📈 The curve y = x^2 is used as an example to illustrate the process of finding the normal line.
  • 🔍 To find the normal line, one must first determine the slope of the tangent line at the given point on the curve.
  • 🔄 The slope of the normal line is the negative reciprocal of the tangent line's slope.
  • 🤔 The point of intersection (x, y) between the normal line and the curve is essential for the calculation.
  • 🧠 The y-coordinate of the intersection point can be found by substituting the x-value into the curve's equation.
  • 📊 The first derivative of the curve's equation provides the slope of the tangent line.
  • 🌟 The point-slope form of a line is used to express the equation of the normal line initially.
  • 📐 The slope-intercept form is derived by rearranging the point-slope equation to solve for y.
  • 📝 A second example is provided where the normal line to the curve y = 3x^2 - 5x - 7 at x = 3 is calculated.
  • 🔍 The process involves finding the y-value for x = 3, calculating the first derivative, and then the slope of the normal line.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to find the equation of a normal line to a curve at a given point.

  • What is the relationship between the slope of a tangent line and the slope of the normal line?

    -The slope of the normal line is the negative reciprocal of the slope of the tangent line.

  • What is the equation of the curve y = x^2?

    -The equation of the curve is y equals x squared.

  • How do you find the y-coordinate of a point on the curve y = x^2 when x = 2?

    -By substituting x with 2 in the equation, the y-coordinate is calculated as 2^3 - 4*2^2 + 5, which simplifies to -3.

  • What is the derivative of the function y = x^3 - 4x?

    -The derivative of the function is 3x^2 - 8x.

  • What is the slope of the tangent line to the curve y = x^3 - 4x at x = 2?

    -The slope of the tangent line at x = 2 is -4, obtained by substituting x with 2 in the derivative of the function.

  • How do you convert the slope of the tangent line to the slope of the normal line?

    -To convert the slope of the tangent line to the slope of the normal line, you change the sign from negative to positive and take the reciprocal of the value.

  • What is the point-slope form of the equation of a line?

    -The point-slope form of the equation of a line is y - y1 = m(x - x1), where m is the slope of the line and (x1, y1) is a point on the line.

  • What is the equation of the normal line to the curve y = 3x^2 - 5x - 7 at x = 3?

    -The equation of the normal line in slope-intercept form is y = (-1/13)x + 68/13.

  • How do you find the y-value of the point where the normal line touches the curve y = 3x^2 - 5x - 7 when x = 3?

    -By substituting x with 3 in the equation of the curve, the y-value is calculated as 3*3^2 - 5*3 - 7, which simplifies to 5.

  • What is the derivative of the function y = 3x^2 - 5x - 7?

    -The derivative of the function is 6x - 5.

Outlines
00:00
📚 Finding the Equation of a Normal Line

This paragraph introduces the concept of finding the equation of a normal line to a curve. It explains the difference between a tangent line, which intersects a curve at a single point, and a normal line, which is perpendicular to the tangent line at the point of intersection. The video provides a step-by-step guide on how to calculate the slope of the normal line by taking the negative reciprocal of the tangent line's slope. It uses the example of the curve y = x^2 and finding the normal line at the point where x = 2. The process involves finding the y-coordinate by substituting the x-value into the curve's equation, calculating the tangent line's slope using the first derivative, and then using the point-slope formula to write the equation of the normal line.

05:02
📝 Solving for the Normal Line on a Practice Problem

The second paragraph continues the discussion by working through another example to find the equation of a normal line. The curve in this example is y = 3x^2 - 5x - 7, and the task is to find the normal line at x = 3. The video demonstrates how to calculate the y-value for the given x-coordinate, determine the slope of the tangent line using the first derivative, and then find the slope of the normal line by taking the negative reciprocal of the tangent line's slope. Finally, it uses the point-slope formula to derive the equation of the normal line in both point-slope and slope-intercept forms.

10:03
🚀 Conclusion and预告 for the Next Video

In the concluding paragraph, the video wraps up the discussion on finding the equation of a normal line and briefly mentions the next topic, which is finding the slope of a secant line. The video encourages viewers to search for the next related video on YouTube using specific keywords, ensuring that the audience knows where to find continued educational content on the subject.

Mindmap
Keywords
💡Normal Line
A normal line is a line that is perpendicular to another line at a given point. In the context of the video, it refers to the line that is perpendicular to the tangent line at a specific point on a curve. The video explains how to find the equation of a normal line to a curve, which is essential for understanding the concept of tangency and perpendicularity in geometry and calculus.
💡Tangent Line
A tangent line is a line that touches a curve at a single point without crossing it. In the video, the tangent line intersects the curve y = x^2 at one point and has a specific slope at that point. The concept of a tangent line is crucial for understanding rates of change and derivatives in calculus.
💡Slope
Slope is a measure of the steepness of a line, indicating the rate of change of the y-values with respect to the x-values. In the video, the slope is used to determine the equation of both the tangent and normal lines to a curve at a given point.
💡Derivative
A derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its variable. In the video, the derivative is used to find the slope of the tangent line to a curve, which is essential for determining the equation of the normal line.
💡Point-Slope Form
The point-slope form is a method of defining a line when given a point on the line and the line's slope. It is used in the video to express the equation of the normal line in terms of its slope and the point where it intersects the curve.
💡Reciprocal
A reciprocal is a mathematical term that refers to the inverse of a number or expression, typically used with fractions. In the context of the video, the negative reciprocal of the tangent line's slope is used to find the slope of the normal line.
💡Curve
A curve is a set of points plotted on a two-dimensional plane that do not form a straight line. In the video, the curve is represented by the equation y = x^2, and the goal is to find the equation of the normal line at a specific point on this curve.
💡Intersection Point
The intersection point is the point at which two lines or a line and a curve meet. In the video, the intersection point is crucial for determining the equation of the normal line, as it provides the coordinates of the point where the normal line touches the curve.
💡First Derivative
The first derivative of a function is the result of differentiating the function with respect to its variable. It is used to find the slope of the tangent line at a specific point on a curve and, by extension, the slope of the normal line.
💡Slope Intercept Form
The slope intercept form is a way to express the equation of a line when the equation is in the form y = mx + b, where m is the slope and b is the y-intercept. In the video, the equation of the normal line is converted to slope intercept form for clarity and simplicity.
💡Power Rule
The power rule is a fundamental calculus rule that allows the differentiation of functions where the variable is raised to a constant power. It states that the derivative of x^n (where n is a constant) is nx^(n-1).
Highlights

The video discusses finding the equation of a normal line to a curve, providing a clear and methodical approach.

The example begins with a curve y = x^2 and finding the normal line at a specific point on the curve.

The tangent line is defined as the line intersecting the curve at one point, and the normal line is perpendicular to it.

The slope of the normal line is the negative reciprocal of the tangent line's slope.

The point of intersection for both the tangent and normal lines is the same.

To find the y-coordinate of the point, the x-value is substituted into the curve's equation.

The slope of the tangent line is calculated by taking the first derivative of the function.

The derivative of x^n is n * x^(n-1), which is used to find the first derivative of the given function.

The first derivative of the function y = x^2 is 2x, and for y = x^3, it is 3x^2.

The slope of the tangent line at x=2 is -4, found by substituting x into the first derivative.

The slope of the normal line is the positive reciprocal of the tangent line's slope, which is 1/4.

The point-slope form of the equation is used to find the equation of the normal line with the known point and slope.

The final equation of the normal line is y = (1/4)x - (3/2), demonstrated through step-by-step calculation.

A second example is provided to illustrate the process of finding the normal line to the curve y = 3x^2 - 5x - 7 at x=3.

The y-value at the point of tangency for the second example is found to be 5, establishing the point (3, 5).

The first derivative for the second example is 6x - 5, used to find the slope of the tangent line.

The slope of the tangent line at x=3 is 13, and the normal line's slope is -1/13.

The point-slope form of the equation for the second example is y - 5 = (-1/13)(x - 3).

The final equation of the normal line for the second example is y = (-1/13)x + 68/13.

The video concludes with a mention of a future video on finding the slope of a secant line.

Transcripts

Browse More Related Video

Equation of a normal line [IB Maths AI SL/HL]

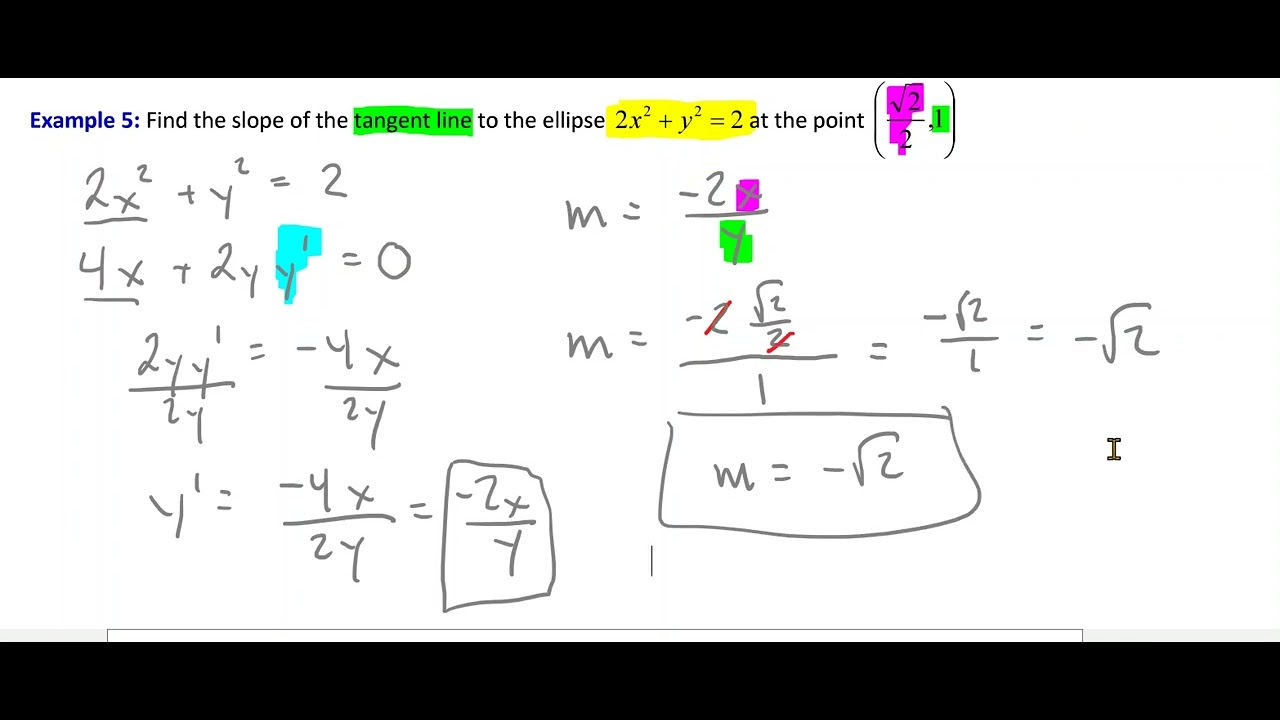
Implicit Differentiation - Finding Equation of Tangent Line

How To Find The Equation of a Tangent Line Using Derivatives - Calculus 1

Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy

Calculus 1: Tangent and Normal Lines Example Problems

Tangent Line to a Polynomial | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusDerivativesNormal LineTangent LineSlope CalculationEquation SolvingEducational ContentVideo TutorialOrganic Chemistry Tutor