Lesson 15 - Calculating Variance in Statistics

Math and Science
29 Mar 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces the concept of variance, distinguishing between sample variance and population variance. It provides a step-by-step guide on how to calculate sample variance using a dataset of five numbers. The process involves finding the mean, calculating deviations from the mean, squaring each deviation, summing them up, and then dividing by the number of samples minus one. The script emphasizes the importance of writing down each step to avoid errors, especially when dealing with larger datasets.

Takeaways
  • 📚 The lesson focuses on understanding the concept of variance, distinguishing between sample variance and population variance.
  • 🔍 Sample variance is calculated using a formula that involves the sum of squared deviations from the mean, divided by n - 1, where n is the number of samples.
  • 📈 Population variance would be calculated if every value in the population was known, but this is often impractical due to the size of the population.
  • 🧮 To calculate variance, first find the mean of the data set by summing all values and dividing by the number of data points.
  • ✍️ When calculating variance, write down each step carefully to avoid errors, especially with larger data sets.
  • 📝 The formula for sample variance is represented as S^2 and involves squaring each deviation before summing them up.
  • 📉 Each data point's deviation from the mean is calculated, then squared, and these squared values are summed for the variance calculation.
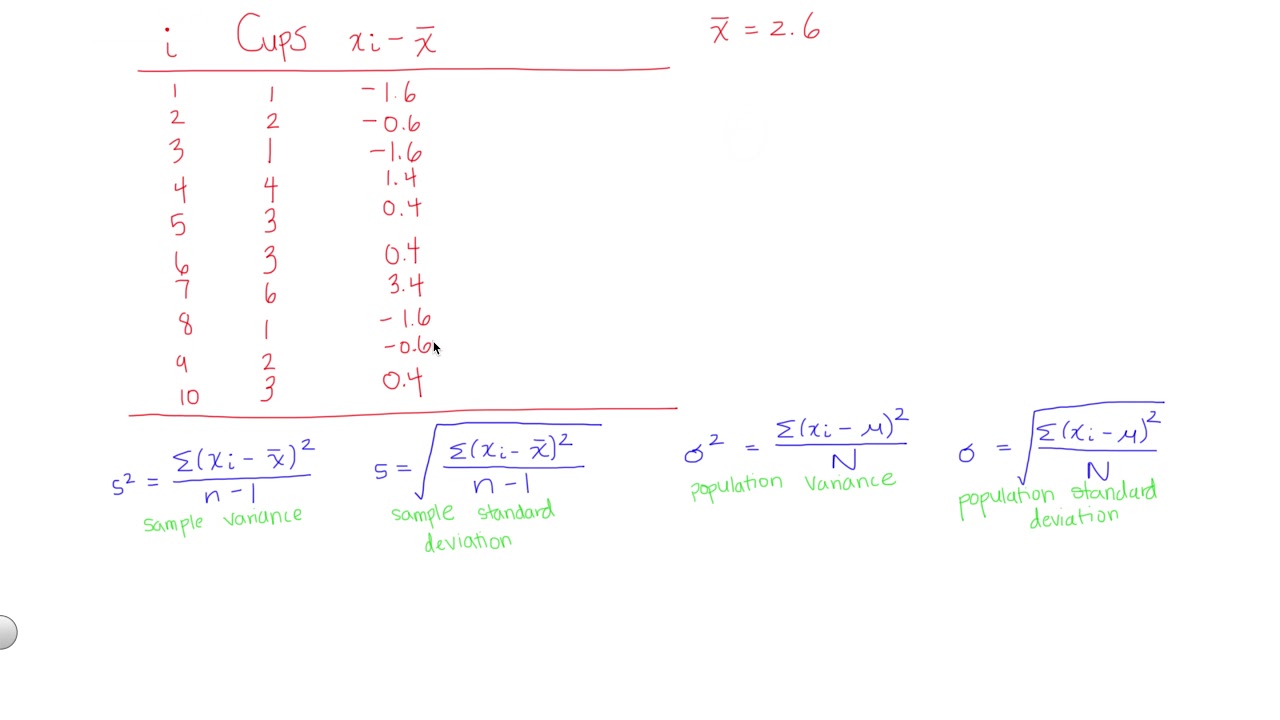
  • 🔢 The provided data set for the example is 5, 8, 7, 6, and 9, and the process involves finding the mean and then calculating the variance.
  • 📊 The mean of the given data set is calculated to be 7, which is used as the reference point for finding deviations.
  • 📌 The script emphasizes the importance of not skipping steps and taking the time to simplify calculations to ensure accuracy.
  • 📝 The script provides a step-by-step guide on how to write out the calculations for variance, highlighting the methodical approach to avoid mistakes.
Q & A

  • What is the difference between sample variance and population variance?

    -Sample variance is calculated when you have a collection of samples, while population variance is calculated when you know every single value in the population. Population variance is rarely calculated because populations are usually too large.

  • Why is it often impractical to calculate the population variance?

    -It is impractical to calculate the population variance because the population is usually too large to know every single value.

  • What is the first step in calculating the sample variance of a data set?

    -The first step in calculating the sample variance is to find the mean of the data set.

  • How do you calculate the mean of a data set?

    -To calculate the mean of a data set, you sum all the values and then divide by the number of values.

  • What is the mean of the data set 5, 8, 7, 6, 9?

    -The mean of the data set 5, 8, 7, 6, 9 is 7.

  • What equation is used to calculate sample variance?

    -The equation used to calculate sample variance is the sum of squared deviations from the mean, divided by the number of samples minus one (n-1).

  • Why is it important to write down each step when calculating variance?

    -It is important to write down each step to avoid mistakes and to ensure that the calculation can be reviewed for accuracy.

  • How do you find the deviations from the mean for each data point?

    -You find the deviations from the mean by subtracting the mean from each data point.

  • What do you do with the deviations before summing them?

    -Before summing the deviations, you square each one.

  • What is the final step in calculating the sample variance after summing the squared deviations?

    -The final step is to divide the sum of the squared deviations by the number of samples minus one (n-1).

Outlines
00:00
📚 Introduction to Variance Calculation

This paragraph introduces the concept of variance, distinguishing between sample variance and population variance. The speaker explains that while population variance is calculated from every value in a large dataset, sample variance is computed from a subset of that population. The focus of the lesson is on calculating sample variance using a specific formula, which involves summing the squared deviations from the mean, divided by the number of samples minus one. The speaker provides an example dataset and emphasizes the importance of finding the mean first, as it is essential for calculating variance. The paragraph concludes with a step-by-step approach to calculating variance, including a reminder to write down each step carefully to avoid errors.

Mindmap
Keywords
💡Variance
Variance is a measure of the dispersion or spread of a set of data points. In the context of the video, it is introduced as a statistical concept that helps understand the distribution of a dataset. The script distinguishes between sample variance and population variance, with the former calculated from a subset of data and the latter from the entire dataset. The video's theme revolves around mastering the calculation of variance, which is essential for statistical analysis.
💡Sample Variance
Sample variance is the variance calculated from a sample of a population. It is an estimate of the population variance and is used when the entire population is too large to measure directly. The script provides a formula for calculating sample variance, emphasizing its importance in statistical analysis and its calculation method using the mean of the sample data.
💡Population Variance
Population variance is the variance of an entire population. It is typically calculated when every single value in the population is known, which is often impractical due to the size of the population. The script mentions this concept in contrast to sample variance, highlighting the limitations in its calculation and its theoretical importance.
💡Mean
The mean, often referred to as the average, is the sum of all data points divided by the number of points. It serves as a central value in a dataset and is crucial for calculating variance. The script demonstrates how to find the mean of a sample, which is a fundamental step in determining the sample variance.
💡Deviation
Deviation refers to the difference between each data point and the mean of the dataset. In the script, deviations are calculated by subtracting the mean from each data point. These deviations are then squared and summed up to find the variance, illustrating their role in quantifying the spread of data points around the mean.
💡S squared Equation
The S squared equation, or the sample variance formula, is used to calculate the variance of a sample. The script explains that this equation involves summing the squared deviations of each data point from the mean and then dividing by the number of samples minus one. It is a key formula in the video's lesson on variance calculation.
💡Data Point
A data point is an individual value or observation within a dataset. The script uses the term to refer to the specific numbers in the sample set, which are used in the calculations of mean and variance. Each data point plays a role in determining the spread and distribution of the dataset.
💡Sample
A sample is a subset of a larger population used for statistical analysis. The script discusses calculating the sample variance, which involves analyzing a sample to infer properties about the entire population. The sample size and its representativeness are important factors in the accuracy of statistical inferences.
💡Calculation
Calculation in this context refers to the process of performing mathematical operations to determine statistical measures such as variance. The script provides a step-by-step guide on how to calculate the sample variance, emphasizing the importance of careful calculation to avoid errors.
💡Statistical Analysis
Statistical analysis is the process of examining and interpreting data to draw conclusions. The video's main theme is mastering statistics, specifically the calculation of variance, which is a fundamental aspect of statistical analysis. The script demonstrates how understanding variance contributes to a deeper analysis of data.
💡Error
In the context of the script, an error refers to a mistake made during the calculation process. The speaker advises against skipping steps and emphasizes the importance of writing down calculations to minimize errors. This highlights the precision required in statistical calculations to ensure accurate results.
Highlights

Introduction to variance and the difference between sample variance and population variance.

Explanation of why population variance is often not calculated due to the large size of the population.

Overview of how to calculate sample variance using the S squared equation.

Emphasis on the importance of finding the mean before calculating variance.

Demonstration of calculating the mean of a sample data set.

Advice on writing down all steps when calculating variance to avoid errors.

Step-by-step guide on how to calculate sample variance using a specific data set.

Explanation of the formula for sample variance: sum of squared deviations divided by n-1.

Highlighting the need to square each deviation before summing them up.

Illustration of the process of calculating deviations for each data point from the mean.

Advice on not skipping steps and simplifying calculations to ensure accuracy.

Emphasis on writing down all calculations to track the process and identify mistakes.

Explanation of how to handle the calculation when the data point equals the mean.

Demonstration of squaring the result of each data point minus the mean.

Advice on not relying on mental calculations to avoid potential errors.

Final step of summing up the squared deviations and dividing by n-1 to find the sample variance.

Summary of the importance of careful calculation and documentation in mastering statistics.

Transcripts

Browse More Related Video

Variance - Clearly Explained (How To Calculate Variance)

Variance and Standard Deviation: Sample and Population Practice Statistics Problems

What is Variance in Statistics? Learn the Variance Formula and Calculating Statistical Variance!

How to Calculate Standard Deviation and Variance by Hand

How To Calculate Variance

Variance and Standard Deviation: Why divide by n-1?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsVarianceSample VariancePopulation VarianceCalculationMeanData AnalysisEducationalTutorialMathematics