Physics - Optics: Lenses (4 of 5) Lens Combinations - Converging & Diverging Lenses

Michel van Biezen
1 May 201305:56
EducationalLearning
32 Likes 10 Comments

TLDRThis script explains a lens combination experiment involving both a converging and a diverging lens. The object is placed 50 cm from the first lens, and using ray diagrams, the script demonstrates how to find the image location and calculate magnification. The first image is real and inverted, with a magnification of -0.67. The second image, formed by the diverging lens, is real, inverted, and magnified 4.5 times. The total magnification is -3, indicating an inverted, three times larger final image compared to the original object.

Takeaways
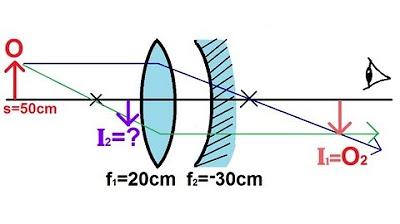
  • 🔍 Lens combination four looks identical to lens combination three but the object is placed differently, at 50 cm from the first lens.
  • 📏 Using ray diagrams, the image location of the first lens is determined.
  • ↔️ Draw a horizontal ray to the converging lens, which then bends to the focal point on the other side.
  • 🔄 Draw another ray from the object through the front focal point, bending horizontally after hitting the lens.
  • 📊 The first image is located using the equation S1' = S1 * F1 / (S1 - F1), resulting in a distance of 33.3 cm.
  • 🔍 The first image is real and inverted, with a magnification of -0.67, indicating it's two-thirds the size of the original object.
  • ↔️ The distance from the first image to the second lens is 23.3 cm, as the image of the first lens becomes the object for the second lens.
  • 📏 The second lens's image location is found using S2' = S2 * F2 / (S2 - F2), yielding a distance of 104 cm.
  • 🔄 The second image is also real and inverted, with a magnification of 4.5 times the size of the second object.
  • 🔍 The total magnification of the system is the product of the individual magnifications, resulting in -3, meaning the final image is three times the size of the original object and inverted.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is the analysis of lens combination number four, which involves both a converging lens and a diverging lens.

  • How does the object's position differ in lens combination number four compared to number three?

    -In lens combination number four, the object is placed 50 cm away from the first lens, which is a different location compared to lens combination number three.

  • What is the focal length of the first lens (F1) in the script?

    -The focal length of the first lens (F1) is 20 cm.

  • How is the image location of the first lens determined using ray diagrams?

    -The image location of the first lens is determined by drawing a horizontal ray until it hits the converging lens and bends to the focal point on the other side, and then continues on.

  • What is the formula used to find the image location (S1') of the first lens?

    -The formula used to find the image location (S1') of the first lens is S1' = S1 * F1 / (S1 - F1).

  • What is the calculated distance to the first image (S1') in cm?

    -The calculated distance to the first image (S1') is 33.3 cm.

  • Why is the first image considered a real image?

    -The first image is considered a real image because it has a positive image distance, indicating that it is formed on the opposite side of the lens from the object.

  • How is the magnification (M1) of the first lens calculated?

    -The magnification (M1) of the first lens is calculated as M1 = -S1' / S1, which in this case is -33.3 cm / 50 cm, resulting in -0.67.

  • What does the magnification of -0.67 signify about the image formed by the first lens?

    -A magnification of -0.67 signifies that the image is inverted and about 2/3 the size of the original object.

  • How is the object distance (S2) for the second lens determined in the script?

    -The object distance (S2) for the second lens is determined by considering the image of the first lens as the object for the second lens, with a negative value since the object is behind the lens, resulting in S2 = -23.3 cm.

  • What is the focal length of the second lens (F2) in the script?

    -The focal length of the second lens (F2) is -30 cm, indicating it is a diverging lens.

  • How is the image location (S2') of the second lens calculated?

    -The image location (S2') of the second lens is calculated using the formula S2' = S2 * F2 / (S2 - F2), resulting in a positive 104 cm.

  • What does the positive value of S2' indicate about the second image?

    -A positive value of S2' indicates that the second image is a real image, formed on the same side of the lens as the object.

  • How is the magnification (M2) of the second lens calculated?

    -The magnification (M2) of the second lens is calculated as M2 = -S2' / S2, resulting in a positive 4.5.

  • What does the magnification of 4.5 signify about the second image?

    -A magnification of 4.5 signifies that the second image is 4.5 times larger than the second object, which is the image of the first lens, and it is also inverted.

  • How is the total magnification of the lens combination calculated?

    -The total magnification of the lens combination is calculated as the product of the magnifications of the two lenses, M_total = M1 * M2, which results in approximately -3.

  • What does the total magnification of -3 indicate about the final image?

    -A total magnification of -3 indicates that the final image is three times larger than the original object and is inverted in direction.

Outlines
00:00
🔍 Explaining Lens Combination Number Four

This paragraph introduces lens combination number four, which is similar to lens combination number three but with a different object placement. The object is positioned 50 cm away from the first lens. The paragraph details the process of locating the first image using ray diagrams and the standard lens equation. The first image distance is calculated as 33.3 cm, and it is a real and inverted image with a magnification of -0.67.

05:01
🔭 Finding the Second Image and Magnification

This paragraph explains the process of finding the second image formed by the second lens. The image from the first lens becomes the object for the second lens, with a distance of -23.3 cm due to its position. Using the lens equation, the second image distance is found to be 104 cm, making it a real image. The magnification of the second lens is calculated as 4.5. The paragraph concludes by determining the total magnification, which is -3, indicating the final image is three times the size of the original object and inverted.

Mindmap
Keywords
💡Lens Combination
A lens combination refers to the arrangement of multiple lenses to work together in focusing light. In the video, the theme revolves around understanding how different lens combinations affect image formation. The script describes a specific lens combination where the object is placed differently, affecting the image location and properties.
💡Object Distance (S1)
Object distance is the distance between the object and the lens. It is a crucial parameter in lens equations and affects the location and properties of the image formed. In the script, the object is placed 50 cm away from the first lens, which is used to calculate the image location and magnification.
💡Focal Point
The focal point is the point where parallel rays of light converge after passing through a lens. It is a fundamental concept in optics and is used to determine the behavior of light through lenses. The script mentions rays bending towards the focal point and the significance of rays passing through the focal point in image formation.
💡Ray Diagrams
Ray diagrams are graphical representations used to visualize the path of light rays through optical systems. They are essential tools in the script for determining the location of the image formed by the lens. The video uses ray diagrams to illustrate how rays from the object interact with the lens to form an image.
💡Image Distance (S1')
Image distance is the distance from the lens to the image formed. It is calculated using lens equations and is a key parameter in understanding the properties of the image. The script calculates S1' using the lens equation to find where the first image is formed relative to the first lens.
💡Magnification (M1)
Magnification is the ratio of the image size to the object size and indicates whether the image is larger or smaller than the object. It is a measure of the change in size and orientation of the image. In the script, the magnification M1 is calculated to determine that the first image is inverted and about 2/3 the size of the original object.
💡Real Image
A real image is formed where light rays actually converge and can be projected onto a screen. The script identifies the first image as real because the calculated image distance is positive, indicating that the light rays converge to form the image.
💡Inverted Image
An inverted image is one where the top and bottom of the image are reversed relative to the object. The script explains that the first image is inverted because the magnification is negative, indicating a flip in the vertical orientation of the image.
💡Diverging Lens
A diverging lens, also known as a concave lens, spreads out light rays. It has a negative focal length and is used in the second part of the lens combination in the script. The lens causes the light rays from the first image to diverge, affecting the formation of the second image.
💡Total Magnification
Total magnification is the product of the magnifications of each lens in a combination. It gives the overall change in size from the original object to the final image. The script calculates the total magnification by multiplying M1 and M2, revealing that the final image is three times larger than the original object but inverted.
💡Converging Lens
A converging lens, also known as a convex lens, bends light rays inward to converge at a focal point. It has a positive focal length and is used in the first part of the lens combination in the script. The lens is responsible for forming the first image, which then becomes the object for the second lens.
Highlights

Lens combination number four is introduced, which appears identical to lens combination number three but with the object placed at a different location.

The object is positioned 50 cm away from the first lens.

Ray diagrams are used to determine the image location of the first lens.

A horizontal ray is drawn from the object until it hits the converging lens, bending to the focal point on the other side.

A second ray is drawn from the object through the focal point on the front side of the lens.

The first image is formed where the two rays meet.

The standard lens equation S1' = S1 * F1 / (S1 - F1) is used to find the location of the first image.

The first image distance S1' is calculated to be 33.3 cm, indicating a real image.

The magnification M1 is found to be -0.67, meaning the image is inverted and about 2/3 the size of the original object.

The distance from the first image to the second lens is determined to be 23.3 cm.

The image of the first lens becomes the object for the second lens, with a negative object distance of -23.3 cm.

The second image is calculated using the equation S2' = S2 * F2 / (S2 - F2) with a diverging lens having a negative focal length.

The second image distance S2' is found to be 104 cm, indicating a real image.

The magnification of the second lens M2 is +4.5, suggesting the image is upright but inverted due to the previous inversion.

The final image is calculated to be 3 times the size of the original object and inverted, as determined by the total magnification M_total = M1 * M2.

The process demonstrates the use of both converging and diverging lenses in a lens combination to achieve specific image properties.

Transcripts

Browse More Related Video

Physics - Optics: Lenses (3 of 5) Lens Combinations - Converging & Diverging Lenses

Physics - Optics: Lenses (1 of 5) Lens Combinations - Two Converging Lenses

Multiple Two Lens System with Diverging and Converging Lens

Physics - Optics: Lenses (3 of 4) Converging Lens

Physics - Optics: Lenses (5 of 5) Lens Combinations - Converging Lens & Mirror

Physics 54 Optics: Mirrors (2 of 6) Concave Mirror

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Lens CombinationOptical PhysicsRay DiagramsImage FormationFocal LengthReal ImageInverted ImageMagnificationConvergent LensDivergent Lens