Calculus AB/BC – 1.16 Intermediate Value Theorem
TLDRIn this calculus lesson, Mr. Bean introduces the Intermediate Value Theorem (IVT), emphasizing its simplicity and common-sense approach. The IVT is applicable to continuous functions over an interval, where the function values at the interval's endpoints are distinct. Mr. Bean illustrates the theorem with various examples, explaining how to determine the minimum number of zeros, or when a function equals a specific value within an interval. He also clarifies that while the IVT ensures the existence of a value within an interval that meets certain conditions, it doesn't guarantee all possible values will be achieved.
Takeaways
- 📚 The lesson is focused on the Intermediate Value Theorem (IVT), a fundamental concept in calculus.
- 📈 The IVT applies to continuous functions, meaning the function must be without breaks or jumps on the interval from A to B.
- 📉 To use IVT, the function's values at the endpoints, f(a) and f(b), must be different, ensuring one is larger and the other smaller.
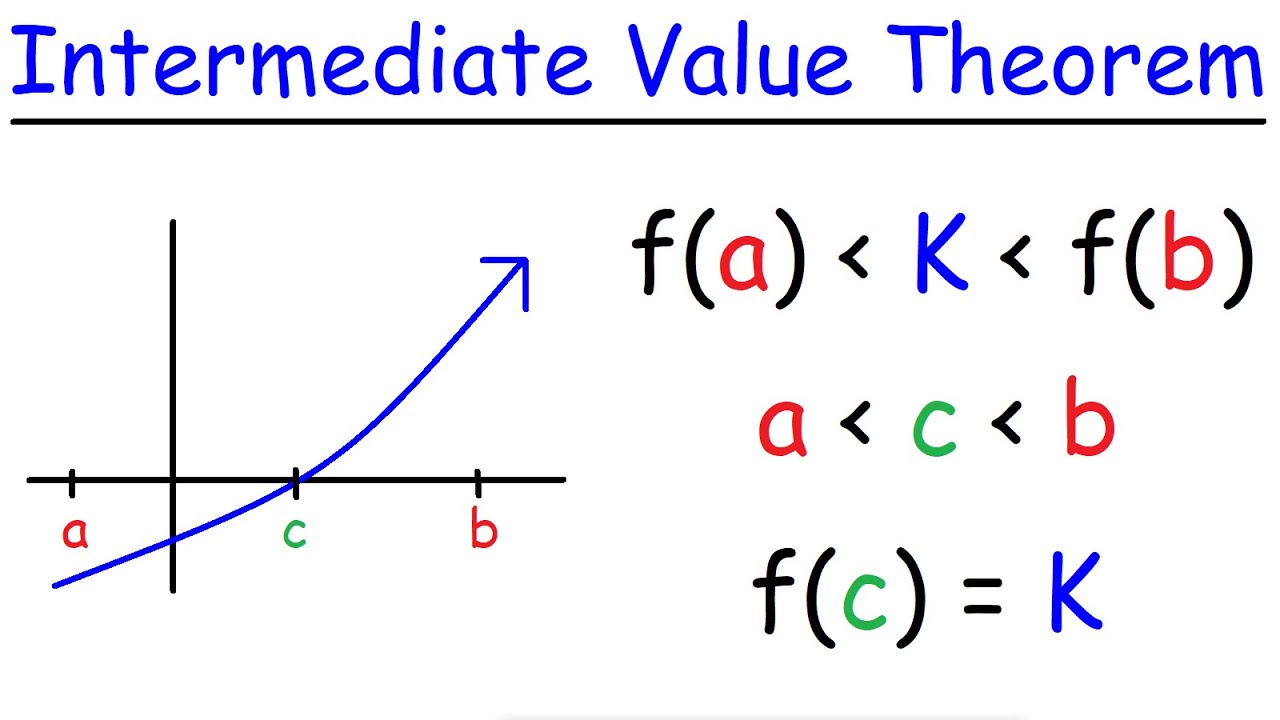
- 🔍 The theorem states that for a continuous function, if f(a) < f(c) < f(b) or f(a) > f(c) > f(b), there exists a value c in the interval (a, b) such that f(c) equals any number between f(a) and f(b).
- 🤔 The IVT is used to determine the existence of roots or specific function values within a given interval without necessarily finding their exact locations.
- 📝 The script provides examples to illustrate the application of IVT, including determining the minimum number of zeros and specific function values within intervals.
- 📉 An example demonstrates that for a continuous function from 0 to 9, there are guaranteed to be at least three zeros due to the nature of the function values crossing zero.
- 🔢 The script clarifies that while the IVT can show the possibility of a function value occurring, it does not guarantee it unless the values at the endpoints straddle the desired value.
- 📌 The IVT is particularly useful for polynomial functions, which are inherently continuous and can be used to determine the existence of specific function values within an interval.
- 📚 The lesson concludes with an example using a polynomial function to show that it must equal eight at some point within the interval from -1 to 5, given the function's continuity and the values at the endpoints.
- 🎓 The script is part of a series of lessons on calculus, aiming to help students understand and apply the IVT in various contexts.
Q & A
What is the main focus of the lesson presented by Mr. Bean?
-The main focus of the lesson is the Intermediate Value Theorem (IVT) in calculus.
Why does Mr. Bean emphasize that the concept of the Intermediate Value Theorem is easy to understand?
-Mr. Bean emphasizes the ease of understanding the IVT because it is based on common sense and does not require complex mathematical justifications for its application.
What is the first condition that must be met for a function to use the Intermediate Value Theorem?
-The first condition is that the function must be continuous on an interval from A to B.
What does Mr. Bean suggest not to draw on the notes during the lesson?
-Mr. Bean suggests not to draw the polynomial graph he is describing, but to focus on a specific part of it from a maximum to a minimum.
What does Mr. Bean use to demonstrate the application of the Intermediate Value Theorem?
-Mr. Bean uses a graph of a polynomial function and specific intervals to demonstrate the application of the IVT.
What is the relationship between the Y values of the endpoints in the context of the IVT?
-For the IVT to work, one of the Y values of the endpoints must be larger and the other smaller, ensuring that there is a range of values between them.
How does Mr. Bean explain the existence of zeros in the context of the IVT?
-Mr. Bean explains that if a function is continuous on an interval and crosses the X-axis, it must have at least one zero within that interval.
What is the minimum number of zeros guaranteed for a function on the interval from 0 to 9 according to the script?
-The minimum number of zeros guaranteed is three, as the function crosses the X-axis at least three times within the given interval.
How does Mr. Bean justify the existence of a value where the function equals two on the interval from 0 to 4?
-Mr. Bean justifies it by showing that the function is continuous and that the Y values at the endpoints of the interval (1 and 3) encompass the value 2, thus according to the IVT, there must be a value C where the function equals two.
What is the conclusion Mr. Bean draws about the possibility of the function equaling negative two on the interval from 4 to 8?
-Mr. Bean concludes that while there is no guarantee that the function will equal negative two, it is possible due to the continuous nature of the function and the range of Y values between 3 and 7.
How does Mr. Bean approach the problem of whether the function can equal eight on the interval from negative one to five?
-Mr. Bean checks the continuity of the function (stating that polynomials are continuous), evaluates the function at the endpoints, and then uses the IVT to conclude that since the function values at the endpoints are 3 and 21, it must cross the value of 8 within the interval.
Outlines
📚 Introduction to the Intermediate Value Theorem
This paragraph introduces the concept of the Intermediate Value Theorem (IVT) in calculus. Mr. Bean, the instructor, assures students that the IVT is an intuitive concept, despite the mathematical justification being more complex. The lesson focuses on the conditions required for a function to be applicable to the IVT, which includes the function being continuous on an interval from A to B, and the Y values at the endpoints being distinct. The instructor uses a polynomial graph as a visual aid, emphasizing a specific segment between a maximum and minimum. The key takeaway is that for a continuous function, if the Y values at the endpoints are different, there must be at least one value within the interval where the function equals a specific number, denoted by a question mark in the script.
🔍 Applying the Intermediate Value Theorem
In this paragraph, the application of the IVT is demonstrated through several examples. The instructor, Mr. Bean, uses the theorem to determine the minimum number of zeros a function can have within specific intervals, and to find the fewest possible times a function equals a particular value. The examples illustrate the theorem's use in identifying the existence of values within a continuous function's range. The instructor also clarifies the difference between 'could' and 'must' in the context of the IVT, noting that while the theorem can guarantee certain values will occur, it cannot ensure all possible values within a range. The final example involves a polynomial function that is guaranteed to equal eight within a given interval, based on the IVT, as the function values at the endpoints are different.
Mindmap
Keywords
💡Intermediate Value Theorem (IVT)
💡Continuous Function
💡Polynomial
💡Roots
💡Interval
💡Endpoints
💡Y-value
💡Graph
💡Maximum and Minimum
💡Mastery Check
Highlights
Introduction to the Intermediate Value Theorem (IVT) by Mr. Bean.
IVT is a concept that is easy to understand but may have complex mathematical justifications.
Focus on a specific part of a polynomial graph from a maximum to a minimum.
Labeling the beginning point as 'a' and the end as 'b' to define the interval [a, b].
Condition for using IVT: the function must be continuous on the interval [a, b].
Y values at endpoints: f(a) and f(b) must be of different magnitudes for IVT to apply.
Introducing a random point 'C' with a Y value between f(a) and f(b).
Existence of a value 'C' in the interval (a, b) such that f(C) equals a given number.
Practical application of IVT to determine the minimum number of zeros on the interval [0, 9].
Explanation of guaranteed zeros when the function crosses from negative to positive values.
Determination of the fewest times f(x) equals one on the interval [4, 9].
Use of IVT to find a value where f(x) equals two on the interval [0, 4].
Justification of the existence of a value 'C' where f(C) equals two using IVT.
Exploration of the possibility of f(x) equaling negative two on the interval [4, 8].
Discussion on the potential existence of negative values without guarantee using IVT.
Application of IVT to determine if the function ever equals eight on the interval [-1, 5].
Quick justification using IVT for the existence of a value 'C' where f(C) equals eight.
Final lesson wrap-up and encouragement for students to master the concept of IVT.
Transcripts
Browse More Related Video

AP Calculus AB - 1.16 Working with the Intermediate Value Theorem

AP Calculus Review Three Theorems You Must Know (EVT, IVT, MVT)
Intermediate Value Theorem

Using the Intermediate Value Theorem Examples

Using the Mean Value Theorem with a Table of Values
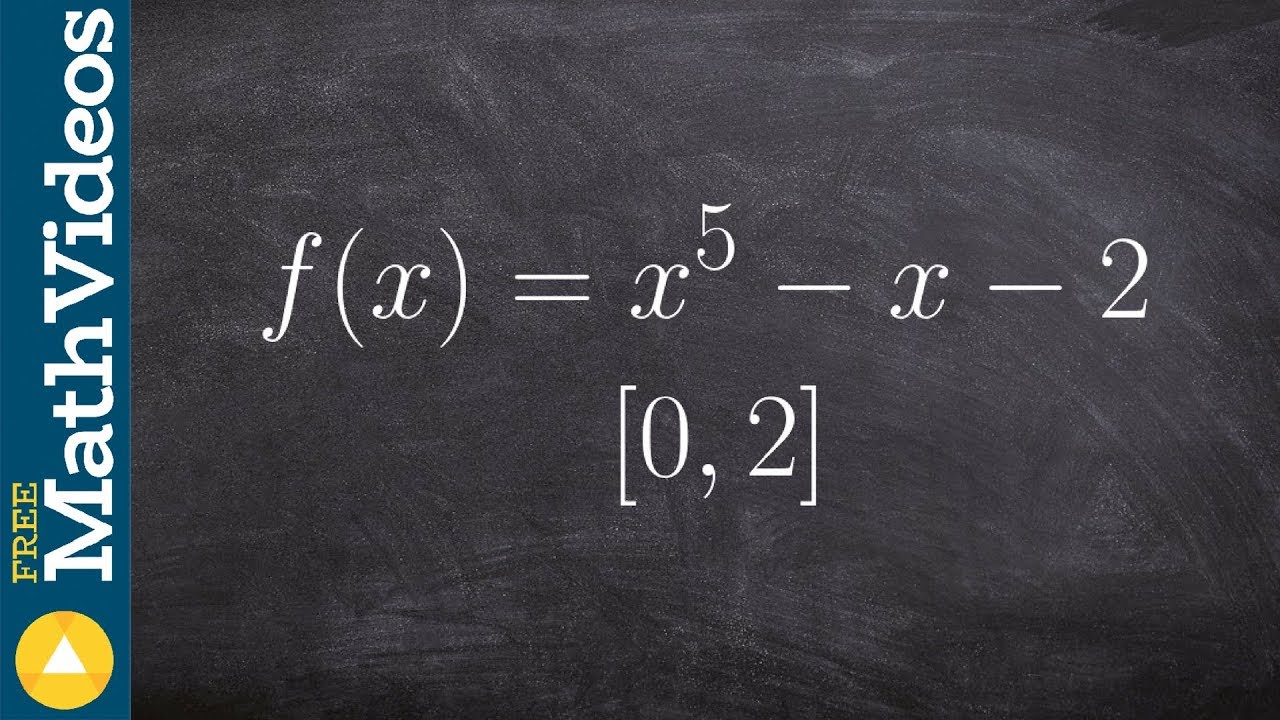
How to show that a solution exists to a functions using IVT
5.0 / 5 (0 votes)
Thanks for rating: