AP Calculus AB: Introduction to Limits

JJ Sandoval
24 Aug 202014:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video introduces the concept of limits in calculus, emphasizing its role in understanding the mathematics of change. The instructor uses the analogy of a road trip to illustrate the idea of average velocity and then transitions to the instantaneous rate of change. The video demonstrates how to find limits numerically, algebraically, and graphically, explaining the notation for approaching a point and how to handle indeterminate forms like 0/0. It also covers the process of rationalizing denominators and factoring to simplify limits, highlighting the importance of mastering these techniques for the AP exam.

Takeaways
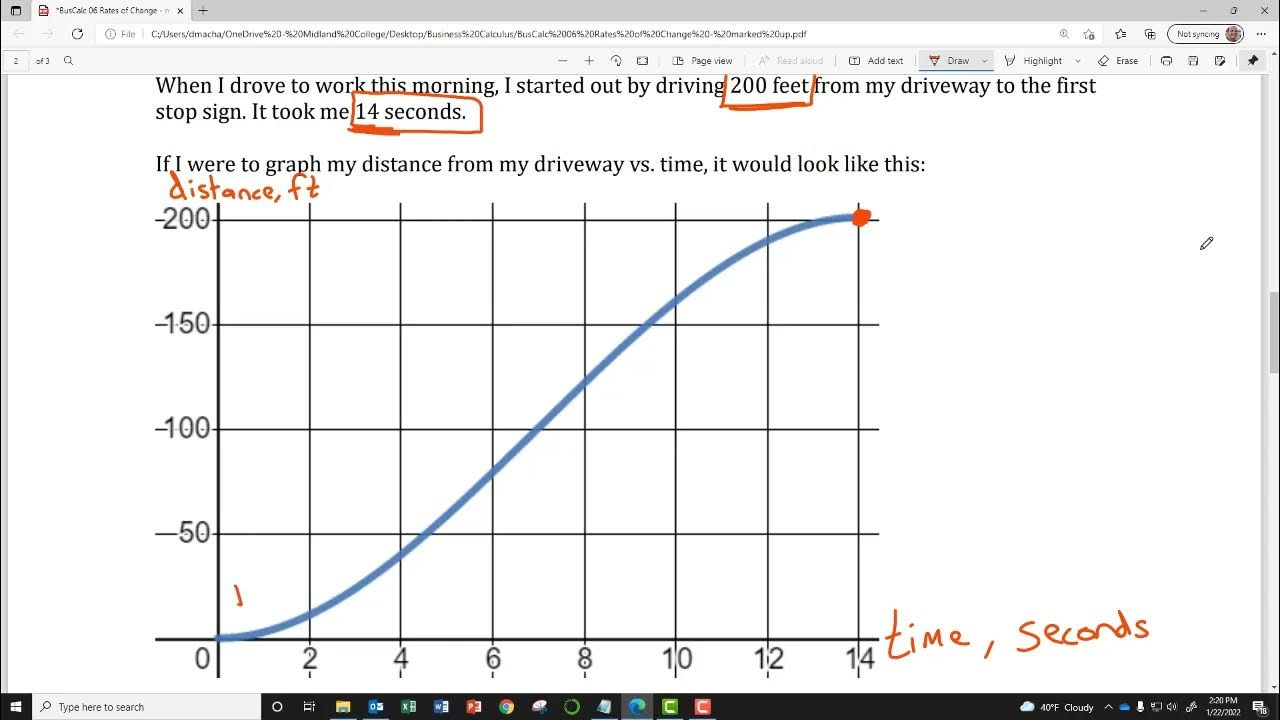
  • 📚 The video introduces the concept of limits in calculus, emphasizing that calculus is the mathematics of change.
  • 🚗 An analogy is used to explain limits, comparing the rate of change to driving up and down a winding mountain road.
  • 🔢 The average velocity is calculated as a simple example using algebra, contrasting with the more complex instantaneous rate of change found in calculus.
  • 📉 The video discusses how calculus can determine the specific velocity at a particular point on a graph, unlike algebra which gives an average.
  • 📌 Limits are introduced as a tool to find the instantaneous position or rate of change, using the function y = 2x - 1 as an example.
  • 📈 The concept of approaching a value without reaching it is explained, using numerical examples to illustrate how limits are calculated from both the left and right sides.
  • 🔍 The importance of checking limits from both directions is highlighted to ensure the function behaves the same way as it approaches a point.
  • 📝 Algebraic methods for finding limits are demonstrated, such as directly substituting the value into the function when possible.
  • 🆚 The difference between numerical and algebraic approaches to finding limits is discussed, with examples to show both methods.
  • ❗ The video points out indeterminate forms like 0/0 and how they require algebraic manipulation to resolve, using factoring as an example.
  • 📚 The notation for limits approaching from the left (a^-) and right (a^+) is explained, which is crucial for understanding limit behavior at discontinuities.
  • 📉 The video concludes by mentioning the three main methods to compute limits: graphically, algebraically, and numerically, noting that all may be tested in an exam setting.
Q & A

  • What is the main topic of this video?

    -The main topic of this video is to introduce the concept of limits in calculus.

  • Why is calculus referred to as the mathematics of change?

    -Calculus is referred to as the mathematics of change because it deals with the study of rates of change and the behavior of functions at a particular point.

  • What is an example given to explain the concept of average velocity?

    -The example given is a road trip where the total distance traveled is 420 miles and it took 6 hours, resulting in an average velocity of 70 miles per hour.

  • How does calculus differ from algebra in terms of dealing with changes in speed or position?

    -Calculus allows for the calculation of specific velocities or rates of change at particular points, whereas algebra deals with average changes over a period.

  • What is the purpose of using limits in calculus?

    -The purpose of using limits in calculus is to find the instantaneous rate of change or position at a specific point, which is not possible with algebra alone.

  • What is the numerical approach to finding the limit of a function as x approaches a certain value?

    -The numerical approach involves getting values of x very close to the specified value from both the left and right sides and observing how the function's output approaches a certain value.

  • How is the notation for limits written when x approaches a number from the left side?

    -The notation for limits when x approaches a number from the left side is written as 'a^-', where 'a' is the number being approached.

  • What does the term 'indeterminate' refer to in the context of limits?

    -The term 'indeterminate' refers to a situation where the expression results in an undefined form, such as 0/0, which does not provide a clear limit.

  • What algebraic tool can be used to simplify an expression that results in an indeterminate form like 0/0?

    -Algebraic tools such as factoring, rationalizing, or using the conjugate can be used to simplify expressions that result in an indeterminate form.

  • Why is it necessary to get rid of radicals in the denominator of a fraction?

    -It is necessary to get rid of radicals in the denominator to simplify the expression and because most professors do not allow radicals to remain in the denominator.

  • What are the three methods mentioned for computing limits?

    -The three methods mentioned for computing limits are numerically using tables, algebraically by simplifying expressions, and graphically by analyzing the graph of the function.

Outlines
00:00
📚 Introduction to Calculus and Limits

The script begins with an introduction to calculus, emphasizing its role in understanding the mathematics of change. The instructor uses the analogy of a road trip to explain the concept of average velocity and how calculus can determine the specific velocity at a particular point. Limits are introduced as a fundamental concept in calculus, which helps in finding the instantaneous rate of change. The example of the function y = 2x - 1 is used to demonstrate how limits can be approached numerically from both sides, illustrating the process of getting closer to a point without actually reaching it. The concept of the left and right limits is introduced, and the algebraic method of evaluating limits by simply substituting the value into the function is also explained.

05:01
🔍 Understanding Indeterminate Forms and Factoring

This paragraph delves into the complexities of evaluating limits when encountering indeterminate forms, such as 0/0. The instructor uses the example of the function (x^3 - 1)/(x - 1) to show how algebraic manipulation, specifically factoring, can resolve such indeterminate forms. The process of factoring a cubic polynomial is explained, and the concept of a hole in a graph is introduced when a term is canceled out during the simplification process. The importance of understanding the notation for approaching a number from the left and right is highlighted, and the instructor illustrates how to rewrite the limit algebraically to find the correct value.

10:02
📘 Advanced Algebraic Techniques in Limits

The final paragraph focuses on advanced algebraic techniques required to evaluate more complex limits, particularly when dealing with radicals in the denominator. The script explains how to rationalize the denominator by multiplying by the conjugate, which eliminates the radical and simplifies the expression. The instructor provides step-by-step guidance on this process, using the example of 3/√(x - 2) and demonstrates how to simplify the expression to find the limit as x approaches 0. The paragraph concludes with a review of the three methods for computing limits: numerically with tables, algebraically, and graphically, noting that the AP exam tests knowledge of all these methods.

Mindmap
Keywords
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and the accumulation of small quantities to model physical phenomena. In the video, calculus is introduced as the 'mathematics of change,' highlighting its importance in understanding the rate of change at specific points, such as the velocity of a vehicle at a particular moment during a trip.
💡Limits
Limits are a fundamental concept in calculus that describe the value that a function or sequence 'approaches' as the input or index approaches some value. The video script uses the concept of limits to explain how to determine the instantaneous rate of change, such as the velocity of a car at a specific point during a journey.
💡Average Velocity
Average velocity is calculated by dividing the total distance traveled by the time taken. In the script, the concept is used to illustrate a simple algebraic calculation before introducing the more complex idea of instantaneous velocity, which requires calculus.
💡Instantaneous Rate of Change
Instantaneous rate of change refers to the derivative of a function at a specific point, which is a measure of how the function changes at that point. The video script explains that calculus is used to find this rate at a particular moment, such as the exact speed of a car at a specific point on a trip.
💡Numerical Approach
A numerical approach to finding limits involves calculating the function's output for values that get progressively closer to the point of interest without actually reaching it. The script demonstrates this by showing how values approach a certain limit from both the left and right sides.
💡Algebraic Approach
The algebraic approach to finding limits involves manipulating the function's expression to directly evaluate the limit. The script provides examples of how to use algebraic techniques, such as factoring, to simplify expressions and find limits.
💡Indeterminate Form
An indeterminate form, such as 0/0, occurs when the direct substitution of a value into a function results in an undefined expression. The script explains how to resolve indeterminate forms by using algebraic techniques to rewrite the expression in a form that allows the limit to be evaluated.
💡Factoring
Factoring is an algebraic method used to break down a polynomial into a product of simpler polynomials or expressions. In the script, factoring is used as a technique to simplify expressions and resolve indeterminate forms, such as in the example of x^3 - 1.
💡Conjugate
The conjugate of an expression is obtained by changing the sign of the radical or imaginary part. In the context of the video, the conjugate is used to eliminate square roots in the denominator of a fraction by multiplying the numerator and denominator by the conjugate, thus simplifying the expression.
💡Graphical Approach
The graphical approach to finding limits involves analyzing the graph of a function to determine the behavior as the input approaches a certain value. The script mentions this approach as one of the methods tested in the AP exam, suggesting its importance in visualizing the concept of limits.
💡Hole
A hole in the graph of a function occurs when the function is undefined at a particular point, resulting in a gap in the graph. The script uses the example of x^3 - 1 to illustrate how factoring can lead to a hole in the graph at x = 1, as the factored terms cancel out, leaving the function undefined at that point.
Highlights

Introduction to the concept of limits in calculus as the mathematics of change.

Using a road trip analogy to explain the concept of average velocity and its relation to calculus.

Differentiating between average velocity and the instantaneous rate of change in calculus.

Numerical approach to finding limits by getting as close as possible to a specific point without reaching it.

Explanation of the left and right limits and their significance in determining the limit of a function.

Demonstration of finding the limit of a linear function y = 2x - 1 as x approaches 3.

Algebraic method of finding limits by simply plugging in the value of x into the function.

Handling indeterminate forms like 0/0 by using numerical tables to approach the point from both sides.

Illustration of the limit process with the function (x^3 - 1) / (x - 1) and its factoring.

Introduction of the notation for limits approaching from the left (-) and right (+).

Clarification of the difference between the algebraic result and the limit result in the case of 0/0.

Use of algebraic manipulation to resolve indeterminate forms and find the true limit.

Example of rationalizing the denominator to simplify expressions involving square roots.

Multiplication by the conjugate to eliminate square roots in the denominator of a fraction.

Demonstration of the limit process for a function with a square root in the denominator as x approaches 0.

Highlighting the three methods to compute limits: graphically, algebraically, and numerically.

Emphasis on the importance of understanding all three methods for the AP exam.

Transcripts

Browse More Related Video

AP Calculus AB - 1.6b Determining Limits Using Algebraic Manipulation

AP Daily: AP Calculus BC (1.1)

AP Daily: AP Calculus AB (1.1)

1.1 - Numerical and Graphical Limits

Ch. 13.2 Finding Limits Algebraically

BusCalc 06 Rates of Change

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus BasicsLimitsRate of ChangeRoad Trip AnalogyInstantaneous VelocityNumerical ApproachAlgebraic MethodIndeterminate FormsFactoring TechniquesRationalizing DenominatorsEducational Content