Graphing the Arctan Function | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this recitation, the focus is on correcting a mistake made during the graphing of the arctangent function in a previous lecture. The instructor clarifies the relationship between the arctangent (or inverse tangent) and the tangent function, emphasizing the unique intersection of their graphs at the origin. The discussion highlights the properties of the tangent function, such as its slope and how it is always greater than x for positive x, leading to the reflection of the arctangent graph below the line y=x, with asymptotes at ±π/2. The summary aims to provide a clearer understanding of the arctangent function's graph and its characteristics.
Takeaways
- 📚 The lecture is a follow-up on the graphing of trigonometric and inverse trigonometric functions, specifically focusing on correcting an error made in the graph of the arctangent function.
- 🔍 The arctangent function is the inverse of the tangent function and can be written as arctan(x) or tan^(-1)(x), both representing the same mathematical operation.
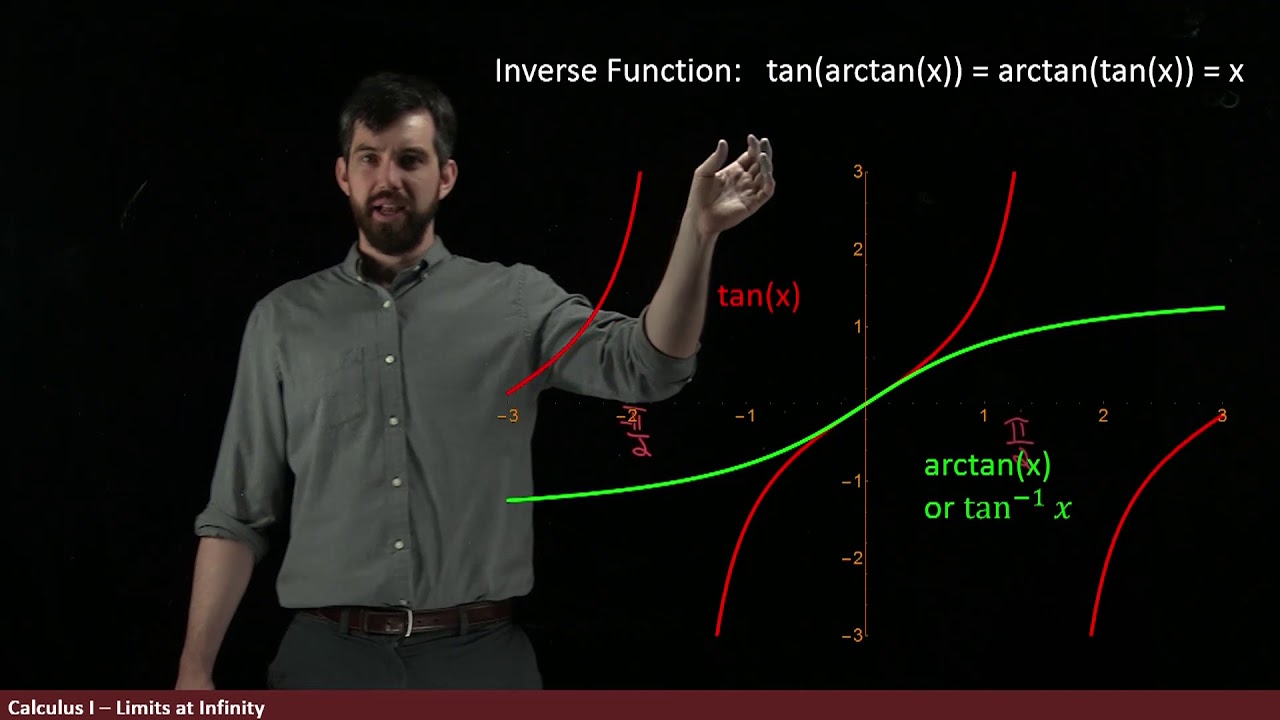
- 📈 The script includes a visual explanation of the graph of y = tan(x), including its asymptotic behavior at π/2 and its periodic nature.
- 📉 The tangent function's graph approaches infinity as x approaches π/2 from the right, and similarly at negative angles, indicating the function's unbounded nature.
- 🤔 The tangent function is tangent to the line y = x at the origin, with a slope of 1 at x = 0, derived from the secant squared function.
- 📊 For positive x, the tangent function is always greater than x, which is a key property used to understand the reflection of the graph for arctan(x).
- 🔄 The reflection of the tangent function's graph across the line y = x results in the graph of the arctangent function.
- 📌 The arctangent graph lies below the line y = x for positive x values, due to the properties of the tangent function mentioned earlier.
- 🚫 The corrected graph emphasizes that the curves y = tan(x) and y = arctan(x) only intersect at the origin, contrary to the earlier incorrect depiction.
- 🔄 At the origin, both functions have a derivative of 1, indicating a point of tangency and the only intersection point.
- ➡️ For negative x values, the relationship between x, tan(x), and arctan(x) reverses, with arctan(x) being greater than x, which in turn is greater than tan(x).
- 📝 The presenter provides a clearer picture of the arctan(x) graph by correcting the previous error and emphasizing the unique intersection at the origin.
Q & A
What was the main topic discussed in the lecture?
-The main topic discussed in the lecture was the graphing of trigonometric functions, specifically focusing on the arctangent or inverse tangent function and correcting an error made in a previous graph.
What is the alternative notation for arctangent mentioned in the script?
-The alternative notation for arctangent mentioned in the script is 'tan to the minus 1', which is equivalent to 'arctan'.
What is the relationship between the tangent function and its inverse, the arctangent function?
-The arctangent function is the inverse of the tangent function. It is used to find the angle whose tangent is a given number.
Why does the graph of y equals tangent of x have asymptotes?
-The graph of y equals tangent of x has asymptotes because the function approaches infinity as x approaches π/2 from the right and negative infinity as x approaches -π/2 from the left, making these points unreachable and thus creating asymptotes.
What is the significance of the slope of the tangent function at the origin?
-The slope of the tangent function at the origin is 1, which is the derivative of tan(x) at x=0. This is significant because it indicates that the tangent function is tangent to the line y=x at the origin.
Why is the graph of arctangent reflected across the line y=x?
-The graph of arctangent is reflected across the line y=x to represent the inverse relationship of the tangent function. This reflection shows that for positive x, the value of arctan(x) is less than x.
What is the horizontal asymptote of the arctangent function?
-The horizontal asymptote of the arctangent function is at π/2 for positive values and -π/2 for negative values, indicating the values that the function approaches but never reaches.
How does the script clarify the error in the previous graph of arctangent?
-The script clarifies the error by explaining that the arctangent function only intersects the line y=x at the origin, unlike the square root and x squared functions which intersect at a later point.
What is the relationship between the derivative of the tangent function and the secant function?
-The derivative of the tangent function, d/dx of tan(x), is equal to secant squared of x, which indicates the rate of change of the tangent function.
How does the script use the concept of reflection to explain the graph of arctangent?
-The script uses the concept of reflection to explain that when the graph of the tangent function is reflected across the line y=x, it results in the graph of the arctangent function, which lies below the line y=x for positive x values.
Why is it important to understand the relationship between the tangent and arctangent functions when graphing them?
-Understanding the relationship between the tangent and arctangent functions is important for accurate graphing because it helps in determining the correct placement of asymptotes, the slope at the origin, and the overall shape of the inverse function's graph.
Outlines
📚 Correction of arctan Graph Error
This paragraph discusses a correction needed for a graph of the arctangent function presented in a previous lecture. The speaker clarifies the notational difference between 'arctan' and 'tan^-1', emphasizing they represent the same inverse tangent function. The focus is on the graphical representation of arctan, highlighting the error in a previous graph where the curves intersected incorrectly. The correct graph is described, showing the arctan function's behavior, including its asymptotes at ±π/2 and the fact that it lies below the line y=x for positive x values. The correction involves understanding the relationship between the tangent function and its inverse, particularly noting that the tangent function's slope at the origin is 1, and for positive x, tan(x) is greater than x, which in turn is greater than arctan(x). The paragraph concludes by correcting the intersection points of y=tan(x) and y=arctan(x), which should only occur at the origin.
Mindmap
Keywords
💡Recitation
💡Trigonometric functions
💡Inverse trigonometric functions
💡Arctan or arctangent
💡Graph
💡Asymptote
💡Derivative
💡Secant squared
💡Reflection
💡Intersection
💡Periodic function
Highlights
Clarification of a slight error in the graph of arctangent (inverse tangent) function from a previous lecture.
Discussion of the different notations for arctangent: arctan and tan^-1, both representing the same function.
Graph setup includes y=x (diagonal line), y=tan(x) (curve), and an asymptote at pi/2 for y=tan(x).
Explanation of the behavior of tangent function as x approaches pi/2 from the right, approaching infinity.
Observation that the tangent function is tangent to the line y=x at the origin.
Derivative of tan(x) is secant squared x, with the derivative at 0 being 1.
For positive x, tangent of x is larger than x, which is a key property for understanding the arctangent graph.
Reflection of the tangent graph across the line y=x to obtain the arctangent graph.
The arctangent graph lies below the line y=x for positive x due to the reflection.
Identification of pi/2 as the horizontal asymptote for the arctangent function.
The arctangent function intersects the line y=x only at the origin.
Comparison of the incorrect graph from the previous lecture to the corrected one, emphasizing the unique intersection point.
For x > 0, y=tan(x) is always bigger than x, which is always bigger than y=arctan(x).
At the origin, both y=tan(x) and y=arctan(x) have a derivative of 1, indicating a tangential relationship.
For negative x, the relationship between y=arctan(x), x, and y=tan(x) is reversed compared to positive x.
Presentation of a cleaner picture of the arctan(x) function by correcting the previous lecture's misunderstanding.
Transcripts
Browse More Related Video
Limits "at" infinity

Derivative of Inverse Trig Functions via Implicit Differentiation

AP Calculus AB: Lesson 2.6 Tangent Line Approximations

How to Convert From Rectangular Coordinates to Polar Coordinates (Precalculus - Trigonometry 38)

Integrals: Trig Substitution 2

Equation of a tangent line [IB Maths AI SL/HL]
5.0 / 5 (0 votes)
Thanks for rating: