Unit VI: Lec 1 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture introduces 'Techniques of Integration,' focusing on the distinction between knowing a derivative and knowing how to find its original function. The instructor, Herbert Gross, explores various methods for evaluating integrals, including basic integration recipes and the use of trigonometric identities. He demonstrates how to tackle integrals by transforming them into familiar forms, such as using trigonometric and hyperbolic substitutions for sums and differences of squares, and completing the square to simplify quadratic expressions. The lecture emphasizes the importance of recognizing patterns and applying appropriate techniques to evaluate integrals effectively.
Takeaways
- 📚 The video script is part of an MIT OpenCourseWare lecture on 'Techniques of Integration', emphasizing the difference between knowing what to do and knowing how to do it in calculus.
- 🔍 The main aim of the course segment is to develop various techniques to evaluate the inverse derivative, focusing on finding the function 'G' when given its derivative 'f'.
- 📉 The script illustrates the challenge of finding an explicit function 'G' whose derivative is a given function 'f', using the example of 'f(x) = e^(-x^2)'.
- 📈 It explains the process of constructing a function using the second fundamental theorem of integral calculus, as demonstrated with the area under the curve 'y = e^(-t^2)'.
- 🔑 The lecture introduces the concept of 'recipes' for integration, which are methods to find the antiderivative 'G' for different types of functions 'f'.
- 📝 The importance of recognizing and applying the correct substitution to simplify integrals is highlighted, with a focus on the role of trigonometric identities.
- 🧩 The script discusses the use of trigonometric identities to transform integrands into more manageable forms, such as splitting off factors of 'cosine x' or using identities to simplify powers of trigonometric functions.
- 🤔 The challenges of finding the appropriate technique or 'recipe' for a given integral are emphasized, as not all integrals can be easily matched to known forms.
- 📐 The concept of 'completing the square' is introduced as a technique for integrating expressions involving quadratic terms, by rewriting them as the sum or difference of two squares.
- 🔄 The process of making a trigonometric or hyperbolic substitution is shown, where the goal is to transform an integral into a form that can be solved using known antiderivatives.
- 🌟 The script concludes with a review of the importance of practice and insight in applying these integration techniques, as well as the anticipation of more advanced techniques in future lectures.
Q & A
What is the main focus of the 'Techniques of Integration' segment in the course?
-The main focus is to develop various recipes to evaluate the inverse derivative, specifically finding the function 'G' when given a function 'f', and discussing the difference between 'knowing what to do and knowing how to do it' in the context of integration.
Why is it generally not easy to find a function 'G' whose derivative is a given function 'f'?
-It is not easy because, in many cases, the inverse of 'f' may not exist in a familiar form or may require complex techniques and manipulations that are not straightforward, regardless of how skilled one is.
Can you provide an example of a function 'f' and its corresponding area function 'A' as discussed in the script?
-Yes, an example given is 'f(x) = e^(-x^2)'. The area function 'A', constructed using the second fundamental theorem of integral calculus, has 'A''(x) equal to 'e^(-x^2)', meaning 'A' is the function whose derivative with respect to 'x' is 'e^(-x^2)'.
What is the significance of the phrase 'u to the n' in the context of integration?
-The phrase 'u to the n' refers to a class of integrals that can be directly evaluated using a known recipe when the integrand is of the form 'u^n du', where 'u' is a differentiable function of 'x'.
How does the script illustrate the use of trigonometric identities in integration?
-The script illustrates the use of trigonometric identities by showing how to manipulate integrands involving powers of cosine and sine to fit the form 'u^n du', making them easier to integrate.
What is the purpose of using the binomial theorem in the context of the script?
-The binomial theorem is used to expand expressions resulting from trigonometric identities, allowing the integrand to be broken down into terms that can be more easily integrated.
Can you explain the concept of 'trigonometric substitution' as mentioned in the script?
-Trigonometric substitution is a technique used to transform an integral into a more manageable form by substituting a trigonometric function that simplifies the integrand, making it possible to apply known integration recipes.
How does the script connect the concept of completing the square to integration?
-The script connects completing the square to integration by showing how to rewrite a quadratic expression in a form that resembles the sum or difference of two squares, which can then be integrated using known techniques.
What is the role of the identity cosh^2(x) - sinh^2(x) = 1 in hyperbolic substitution as discussed in the script?
-This identity is used to transform an integral involving a quadratic expression into a form that can be integrated using hyperbolic functions, similar to how circular trigonometric substitutions are used.
How does the script emphasize the importance of recognizing structural forms in integration?
-The script emphasizes the importance by showing how recognizing the structural forms of expressions, such as the sum or difference of two squares, allows for the application of appropriate substitution techniques, leading to successful integration.
Outlines
📚 Introduction to Techniques of Integration
The video begins with an announcer's introduction to MIT OpenCourseWare and a call for donations to support its educational mission. Professor Herbert Gross then introduces a new segment on 'Techniques of Integration,' emphasizing the difference between knowing what to do and how to do it. The focus is on developing methods to find the inverse derivative or integral of a function, given its derivative. The professor uses the example of the function 'G' whose derivative is 'f', and explains the concept of indefinite integrals. The challenges of finding 'G' when 'f' is given are discussed, using the example of the function 'e to the minus x squared'. The goal is to find familiar forms for 'G' for various types of 'f', and the lecture previews the integration techniques to be covered.
🔍 Basic Integration Techniques and U-Substitution
This paragraph delves into basic integration techniques, starting with the integral of a function raised to a power, 'u^n'. The professor explains the importance of matching the integrand with the differential, using 'u' as a generic variable. Examples are given to illustrate how to apply this technique, including a detailed explanation of integrating 'sine x' to the n-th power. The concept of natural substitution is introduced, where 'u' is replaced with 'sine x', and the differential 'du' becomes 'cosine x dx'. The paragraph highlights the need for ingenuity in reducing new integrands to familiar forms and the excitement of tackling unfamiliar integral problems.
📈 Trigonometric Identities in Integration
The role of trigonometric identities in simplifying integration problems is explored. The professor discusses how to handle integrals involving powers of cosine, using the identity for cosine squared and the binomial theorem to break down the integrand into manageable terms. The strategy of separating a factor of 'cosine x' when raised to an odd power is highlighted. The importance of recognizing when to apply trigonometric identities to transform an integral into a familiar form is emphasized, and the process of reducing complex problems into simpler, solvable ones is illustrated.
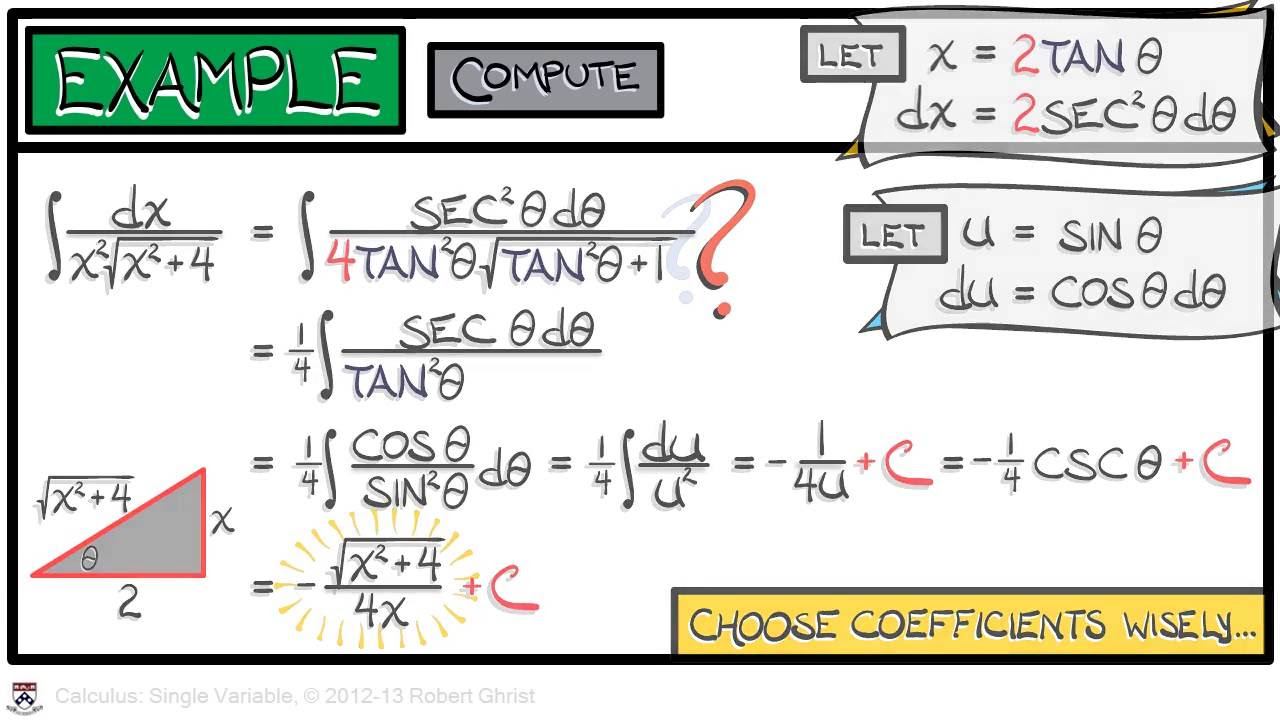
📐 Trigonometric and Hyperbolic Substitutions
This section focuses on the application of trigonometric and hyperbolic substitutions to solve integrals involving sums and differences of squares. The professor uses a right triangle analogy to explain how to transform the integral of the square root of 'a squared minus x squared' into an integral in terms of theta, resulting in the inverse sine function. The concept of hyperbolic substitution is introduced when circular functions are not helpful, using the identity for hyperbolic cosine and sine. The professor demonstrates how to transform the integral of the square root of 'x squared minus a squared' using hyperbolic functions, leading to the inverse hyperbolic cosine function.
🔑 The Power of Structural Insight in Integration
The paragraph emphasizes the importance of recognizing structural similarities between trigonometric and hyperbolic functions when performing substitutions. The professor illustrates how the identity involving cosecant and cotangent is analogous to the one involving cosh and sinh, which aids in making the correct substitution. The process of transforming an integral involving 'x squared minus a squared' into a simpler form using hyperbolic functions is detailed, demonstrating how to arrive at the inverse hyperbolic cosine function as the solution.
📉 Completing the Square and Its Relevance to Integration
The final paragraph of the script introduces the technique of completing the square in the context of integration. The professor explains how to transform a quadratic expression 'ax squared plus bx plus c' into a perfect square plus a constant by adding and subtracting the square of half the coefficient of 'x'. This method is shown to be useful in rewriting an integrand involving a quadratic expression, allowing it to be expressed in a form that resembles the sum or difference of two squares, which can then be integrated using previously discussed techniques.
🌟 Conclusion and Call to Support MIT OpenCourseWare
The video concludes with a summary of the techniques introduced for solving integrals, emphasizing the importance of reducing new problems to familiar ones. The professor hints at more elaborate recipes to be covered in the next lecture. The announcer returns to thank the Gabriella and Paul Rosenbaum Foundation for funding the video's publication and encourages viewers to donate to MIT OpenCourseWare to ensure continued free access to educational content.
Mindmap
Keywords
💡Creative Commons license
💡Techniques of Integration
💡Indefinite Integral
💡Second Fundamental Theorem of Integral Calculus
💡Trigonometric Identities
💡Binomial Theorem
💡Trigonometric Substitution
💡Inverse Circular and Hyperbolic Functions
💡Completing the Square
💡Sum and Difference of Squares
Highlights
Introduction of a new segment on 'Techniques of Integration' emphasizing the difference between knowing what to do and how to do it.
The aim to develop various recipes for evaluating the inverse derivative, focusing on finding 'G' when given 'f'.
Illustration of the challenge in finding an explicit function 'G' whose derivative is a given function 'f'.
The example of finding an integral for 'e to the minus x squared' using the second fundamental theorem of integral calculus.
The objective of finding 'G of x' for various types of 'f of x' using familiar forms.
Review of basic integration techniques such as integral of 'u to the n' du and handling the case when 'n' equals -1.
Importance of recognizing the need for algebraic manipulation to match integrals to known forms.
Technique of splitting off a factor of 'cosine x' when dealing with powers of trigonometric functions.
Use of trigonometric identities to transform integrands into more manageable forms.
The process of reducing unfamiliar integrals to familiar ones through various algebraic and trigonometric techniques.
Handling of sums and differences of squares using trigonometric and hyperbolic substitutions.
Motivation behind trigonometric substitution and its application in integral calculus.
The connection between hyperbolic functions and the strategy for handling integrals involving the square root of 'x squared minus a squared'.
The analytical approach to hyperbolic substitutions and its relation to circular functions.
Technique of completing the square to simplify the integration of quadratic expressions.
The method of converting a quadratic expression into a sum and/or difference of two squares for easier integration.
Conclusion of the lesson with a preview of more elaborate recipes to be introduced in the next lecture.
Transcripts
Browse More Related Video
Calculus Chapter 3 Lecture 23 Trig Substitution

Lec 27 | MIT 18.01 Single Variable Calculus, Fall 2007

Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems
Trig Integral Practice | MIT 18.01SC Single Variable Calculus, Fall 2010
Integration by completing the square | MIT 18.01SC Single Variable Calculus, Fall 2010

Calculus AB Unit 6 Review
5.0 / 5 (0 votes)
Thanks for rating: