More on moment of inertia | Moments, torque, and angular momentum | Physics | Khan Academy

Khan Academy Physics
29 Jul 201614:59
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of moment of inertia, emphasizing its significance in determining an object's resistance to angular acceleration. It explains that moment of inertia is intrinsic to rotational inertia and is pivotal in Newton's second law of motion in its angular form. The script clarifies that moment of inertia varies with the distribution of mass relative to the axis of rotation, using examples of point masses, rods, cylinders, and spheres to illustrate different calculation formulas. It highlights how moving mass closer to the axis or reducing mass can decrease moment of inertia, making rotation easier. The use of calculus for continuous objects is mentioned, with specific formulas provided for various geometries and axes of rotation.

Takeaways
  • 🌟 The moment of inertia is a measure of an object's resistance to angular acceleration, representing its rotational inertia.
  • 📐 The formula for moment of inertia for a point mass is given by I = mr², where m is the mass and r is the distance from the axis of rotation.
  • 🔄 For multiple point masses, the total moment of inertia is the sum of the individual moments of inertia (I = m₁r₁² + m₂r₂² + ... + mₙrₙ²).
  • 🎾 The moment of inertia can be reduced by moving the mass closer to the axis of rotation, making the object easier to rotate.
  • 🏌️ For extended objects like rods or cylinders, calculus is used to determine the moment of inertia, which differs from the point mass formula.
  • 🔧 The moment of inertia for a rod rotating about its end is I = (1/3)mL², and for rotation about its center, it's I = (1/12)mL².
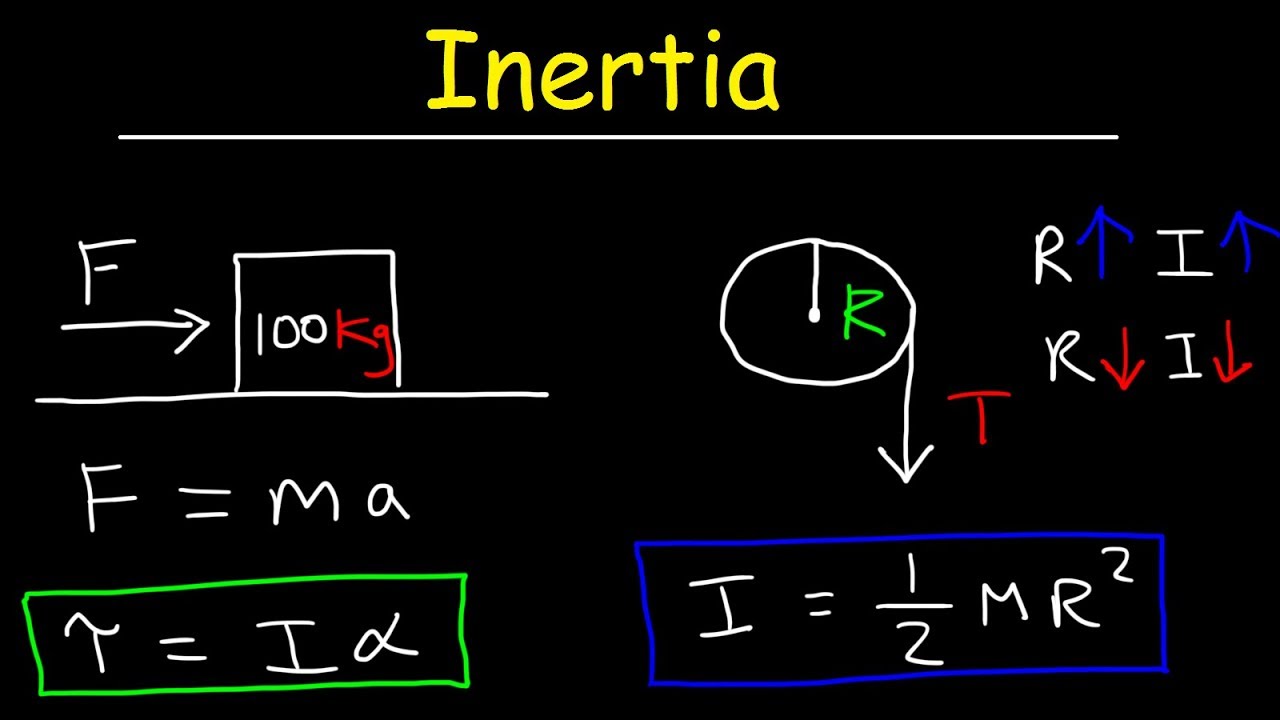
  • 🔄 For a cylinder rotating about its center, the moment of inertia is I = (1/2)mr², where m is the mass and r is the radius.
  • 🌐 For a sphere rotating about an axis through its center, the moment of inertia is I = (2/5)mr².
  • 📈 The distribution of mass within an object affects its moment of inertia; objects with mass distributed closer to the axis of rotation have a lower moment of inertia.
  • 📚 The axis of rotation is a critical factor in determining the moment of inertia; different axes yield different values.
  • 🔍 Reference materials such as textbooks or online resources often provide charts listing the moments of inertia for various objects and their respective axes.
Q & A

  • What is the moment of inertia in physics?

    -The moment of inertia, also known as rotational inertia, is a measure of an object's resistance to angular acceleration. It indicates how difficult it is to speed up or slow down an object's rotation.

  • How does the moment of inertia relate to Newton's second law in rotational motion?

    -In the angular version of Newton's second law, the angular acceleration is equal to the net torque divided by the moment of inertia. This highlights the role of moment of inertia as the rotational counterpart to mass in linear motion.

  • What is the formula for the moment of inertia of a point mass in circular motion?

    -The moment of inertia for a point mass in circular motion is given by the formula mr^2, where m is the mass and r is the distance from the axis of rotation.

  • How do you calculate the moment of inertia for a system with multiple point masses?

    -For a system with multiple point masses, you can calculate the total moment of inertia by summing the contributions from each individual point mass using the formula mr^2 for each mass and its respective distance from the axis.

  • How does the position of mass affect the moment of inertia?

    -The position of mass greatly affects the moment of inertia. If masses are moved closer to the axis of rotation, the moment of inertia decreases, making the object easier to rotate. Conversely, moving masses away from the axis increases the moment of inertia.

  • What is the moment of inertia for a rod rotating about its end?

    -The moment of inertia for a rod rotating about its end is given by the formula (1/3) mL^2, where m is the total mass of the rod and L is its length.

  • How does rotating an object about its center change its moment of inertia compared to rotating about its end?

    -Rotating an object about its center typically results in a lower moment of inertia compared to rotating about its end. This is because more mass is closer to the axis of rotation when the object is rotated about its center, leading to smaller radii and thus a lower moment of inertia.

  • What is the moment of inertia for a cylinder rotating about its center?

    -The moment of inertia for a cylinder rotating about its center is given by the formula (1/2) mr^2, where m is the mass and r is the radius of the cylinder.

  • How does the shape of an object affect its moment of inertia?

    -The shape of an object affects its moment of inertia because different shapes have different mass distributions relative to the axis of rotation. For example, a sphere has a moment of inertia of (2/5) mr^2 when rotating about its center, which is different from the formulas for rods, cylinders, and point masses.

  • What is the moment of inertia for a sphere rotating about its center?

    -The moment of inertia for a sphere rotating about its center is given by the formula (2/5) mr^2, where m is the mass and r is the radius of the sphere.

  • Why do continuous objects like rods, cylinders, and spheres have moments of inertia less than mL^2 or mr^2?

    -Continuous objects have moments of inertia less than mL^2 or mr^2 because not all mass is rotating at the maximum radius. Some mass is closer to the axis of rotation, resulting in smaller radii and reduced contributions to the overall moment of inertia.

Outlines
00:00
🌟 Understanding Moment of Inertia

This paragraph introduces the concept of moment of inertia, highlighting its significance in determining the resistance of an object to angular acceleration. It explains that a larger moment of inertia makes an object more resistant to changes in its rotational speed, while a smaller one indicates ease of angular acceleration. The paragraph also discusses the relevance of moment of inertia in Newton's second law for angular motion, where it is the denominator in the formula for angular acceleration (alpha). The analogy of a point mass is used to simplify the calculation of moment of inertia, emphasizing that it can be treated as if all the mass is concentrated at a certain distance from the axis of rotation. The formula for calculating moment of inertia for a point mass in circular motion is presented as mass times the square of the distance from the axis.

05:02
🔄 Calculating Moment of Inertia for Distributed Masses

The second paragraph delves into the calculation of moment of inertia for systems with multiple point masses. It explains that the total moment of inertia is the sum of the individual moments of inertia for each point mass, using the formula m times r squared. The paragraph uses an example of three point masses to illustrate how to calculate the total moment of inertia by adding up the contributions from each mass. It also discusses the impact of mass distribution on the ease of rotation, suggesting that moving masses closer to the axis of rotation reduces the moment of inertia, making the system easier to rotate. The example of a baseball bat is used to illustrate this concept, showing that swinging the bat from the end where the mass is concentrated near the axis results in less moment of inertia and easier rotation.

10:02
📐 Moment of Inertia for Continuous Objects

This paragraph addresses the challenge of calculating the moment of inertia for continuous objects, such as a rod or a cylinder, where mass is distributed throughout the object. It explains that the formulas for point masses cannot be applied and instead, calculus is required to derive the moment of inertia for these shapes. The paragraph provides the results for the moment of inertia for a rod rotating about its end (1/3 mL squared) and about its center (1/12 mL squared), and for a cylinder rotating about its center (1/2 mr squared). It also discusses the impact of the axis of rotation on the moment of inertia, emphasizing that the location of the axis significantly affects the calculation. The paragraph concludes with the formula for the moment of inertia of a sphere rotating about an axis through its center, which is 2/5 mr squared. The key takeaway is that the distribution of mass within an object affects its moment of inertia, with mass closer to the axis contributing less to the total inertia.

Mindmap
Keywords
💡Moment of Inertia
The moment of inertia, also known as rotational inertia, is a measure of an object's resistance to changes in its angular velocity. It is a crucial concept in physics that describes how difficult it is to angularly accelerate an object. In the context of the video, the moment of inertia is used to explain the rotational motion of various objects and systems, such as point masses, rods, cylinders, and spheres. The formula for moment of inertia for a point mass is given as 'mr^2', where 'm' is the mass and 'r' is the distance from the axis of rotation.
💡Angular Acceleration
Angular acceleration is the rate of change of angular velocity. It is a key concept in the study of rotational motion and is directly related to the moment of inertia and the net torque applied on an object. The video explains that according to the angular version of Newton's second law, angular acceleration is equal to the net torque divided by the moment of inertia. This means that an object with a larger moment of inertia will have a smaller angular acceleration for the same amount of torque.
💡Net Torque
Net torque is the resultant force that causes an object to rotate around an axis. It is calculated as the sum of all individual torques acting on the object. In the context of the video, net torque is used in conjunction with the moment of inertia to determine the angular acceleration of an object. The greater the net torque, the greater the angular acceleration, assuming the moment of inertia remains constant.
💡Point Mass
A point mass is an idealized physical model that represents an object with mass concentrated at a single point in space. In the context of the video, point masses are used to simplify the calculation of moment of inertia for objects rotating around an axis. The video explains that for a point mass rotating in a circle, the moment of inertia is simply the mass times the square of the distance from the axis.
💡Rotational Inertia
Rotational inertia is another term for moment of inertia, which quantifies an object's tendency to maintain its state of rotation. It is a fundamental concept in the study of rotational dynamics. The greater the rotational inertia, the more difficult it is to change the object's rotational state, whether by speeding up, slowing down, or changing the direction of rotation. The video emphasizes the importance of understanding rotational inertia to predict and control the rotational motion of objects.
💡Newton's Second Law (Angular Version)
Newton's second law, in its angular version, relates the angular acceleration of an object to the net torque acting on it and its moment of inertia. It states that the angular acceleration is equal to the net torque divided by the moment of inertia. This law is fundamental in understanding how rotational forces affect the motion of objects and is a key theme in the video.
💡Rod
In the context of the video, a rod is a linear object that may have mass distributed along its length. The moment of inertia for a rod rotating about an axis at its end is different from that of a point mass or a rod rotating about its center. The video explains that the moment of inertia for a rod about its end is 1/3 mL^2, where 'm' is the mass and 'L' is the length of the rod.
💡Cylinder
A cylinder, as discussed in the video, is a geometric shape with mass distributed evenly throughout its volume. The moment of inertia for a cylinder rotating about its center is different from that of a point mass or a rod. The video explains that the moment of inertia for a cylinder is 1/2 mr^2, where 'm' is the mass and 'r' is the radius of the cylinder.
💡Sphere
A sphere is a three-dimensional geometric shape that is perfectly symmetrical around its center. The video discusses the moment of inertia of a sphere rotating about an axis through its center, which is 2/5 mr^2, where 'm' is the mass and 'r' is the radius of the sphere. This formula accounts for the fact that not all mass is at the same distance from the axis, as some mass is closer to the axis than others.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. In the context of the video, calculus is mentioned as the tool needed to derive the formulas for the moment of inertia of continuous objects, such as rods, cylinders, and spheres, when the mass is not concentrated at a single point. The video suggests that while the formulas for these shapes are available in textbooks and online, understanding calculus allows one to derive these formulas and gain a deeper understanding of the concepts.
💡Axis of Rotation
The axis of rotation is the line around which an object rotates. The position of this axis significantly affects the moment of inertia of an object. The video emphasizes that the moment of inertia depends on the choice of the axis, as different axes result in different distances (rs) from the mass elements to the axis, which in turn affects the rotational inertia.
Highlights

The moment of inertia is also known as rotational inertia, which represents the resistance to angular acceleration.

An object with a large moment of inertia will be difficult to angularly accelerate, whereas an object with a small moment of inertia will be easier to angularly accelerate.

The moment of inertia is a factor in the angular version of Newton's second law, where angular acceleration is equal to the net torque divided by the moment of inertia.

The moment of inertia for a point mass is calculated as mass times the square of the distance from the axis.

For multiple point masses, the moment of inertia is the sum of the contributions from each individual point mass.

The moment of inertia can be reduced by moving masses closer to the axis of rotation, making the object easier to rotate.

The moment of inertia for a rod rotating about its end is 1/3 mL squared.

For a rod rotating about its center, the moment of inertia is 1/12 mL squared.

The moment of inertia for a cylinder (or disc) rotating about its center is 1/2 mr squared.

A sphere rotating about an axis through its center has a moment of inertia of 2/5 mr squared.

The distribution of mass within an object affects its moment of inertia, with mass closer to the axis contributing less to the inertia.

The moment of inertia depends on the axis of rotation, with different formulas for different geometries and axis locations.

Calculus, specifically integrals, is used to derive the formulas for the moment of inertia of continuous objects.

The moment of inertia is crucial in determining the ease or difficulty of rotating an object.

Practical applications of moment of inertia can be seen in everyday objects like baseball bats, where holding closer to the axis allows for faster rotation.

The moment of inertia is a fundamental concept in physics, with wide applications in understanding the dynamics of rotating systems.

For complex geometries, charts with moments of inertia for commonly-shaped objects and their respective axes can be found in textbooks or online.

Transcripts

Browse More Related Video

Moment of Inertia | Physics with Professor Matt Anderson | M12-05

College Physics 1: Lecture 25 - Moment of Inertia and Rotational Dynamics

AP Physics 1 - Rotational Dynamics

Rotational version of Newton's second law | Physics | Khan Academy

Inertia - Basic Introduction, Torque, Angular Acceleration, Newton's Second Law, Rotational Motion

Demonstrating Rotational Inertia (or Moment of Inertia)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Rotational InertiaAngular AccelerationMoment of InertiaPhysics ConceptsMass DistributionPoint MassesRod RotationCylinder MomentSphere InertiaCalculus ApplicationEducational Content