Lec 22: Green's theorem | MIT 18.02 Multivariable Calculus, Fall 2007
TLDRThis script from an MIT OpenCourseWare lecture explores the concept of Green's theorem, a fundamental principle in vector calculus that simplifies the computation of line integrals for closed curves by converting them into double integrals over an enclosed region. The lecture delves into the conditions under which Green's theorem applies, demonstrates its utility through examples, and discusses its historical application in devices like the planimeter for measuring areas on graph paper, highlighting the theorem's significance in both theoretical and practical contexts.
Takeaways
- 📚 The script discusses the concept of the curl of a vector field, which measures how far the field is from being conservative. A zero curl indicates a conservative field.
- 🔍 If a vector field has a curl of zero and is defined everywhere, it is conservative, and the line integral over any closed curve will be zero.
- 📐 Green's theorem provides an alternative method to calculate the line integral over a closed curve by transforming it into a double integral over the enclosed region.
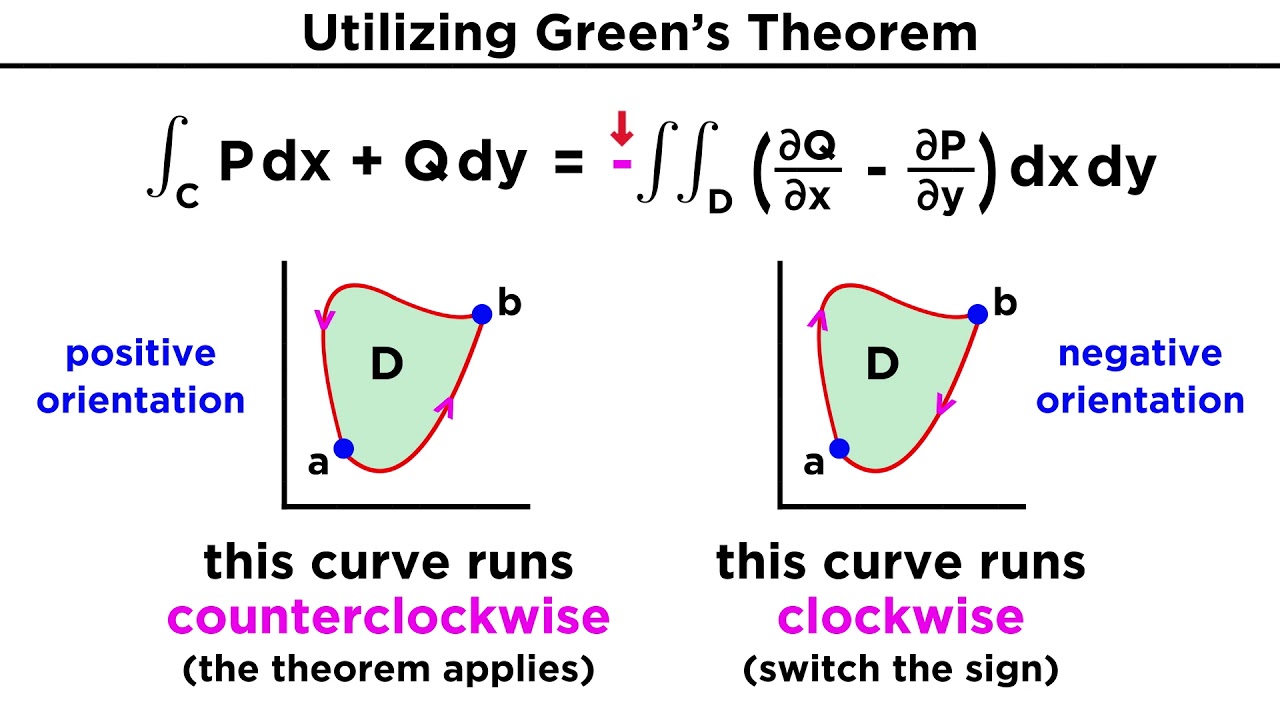
- 🔄 Green's theorem is applicable for closed curves that enclose a region and are traversed counterclockwise, matching the convention of curl definition.
- ⚙️ The proof of Green's theorem involves simplifying the problem by considering special cases and using the properties of vector fields and regions.
- 📉 The script provides an example of calculating a line integral over a circle using Green's theorem, which simplifies the process compared to direct calculation.
- 🤔 The script raises the question of the implications of Green's theorem when applied to vector fields that are not defined everywhere, highlighting potential issues.
- 📝 The proof of Green's theorem is further explained by breaking down the problem into simpler cases and using the concept of vertically simple regions.
- 🔍 The historical application of Green's theorem is demonstrated through the use of a planimeter, a device used to measure areas by performing a line integral.
- 💡 The script concludes with a discussion on how modern computers have made the use of planimeters obsolete, as they can sum up areas more efficiently.
- 📚 The overall takeaway is the importance and utility of Green's theorem in evaluating line integrals and its historical significance in practical applications.
Q & A
What is the curl of a vector field and why is it significant?
-The curl of a vector field is a measure of how much the field is diverging or converging at a particular point. It is significant because if the curl is zero everywhere the field is defined, and the field is defined everywhere, then it is conservative, meaning the line integral around a closed curve will be zero.
What is the condition for a vector field to be conservative?
-A vector field is conservative if its curl is zero everywhere it is defined, and the field is defined over the entire region of interest.
What are the two methods mentioned in the script to compute the line integral along a closed curve?
-The two methods mentioned are direct calculation and using Green's theorem, which can be used to compute the line integral by evaluating a double integral over the enclosed region.
How does Green's theorem relate the line integral of a vector field to a double integral?
-Green's theorem states that the line integral of a vector field around a closed curve is equal to the double integral of the curl of the vector field over the region enclosed by the curve.
What is the significance of the direction of the closed curve in applying Green's theorem?
-The direction of the closed curve is significant because Green's theorem assumes that the curve is traversed counterclockwise. If the curve goes clockwise, the line integral can be converted to a counterclockwise one by taking the negative of the integral.
Why is the curl defined as N sub x minus M sub y and not the other way around?
-The definition of curl as N sub x minus M sub y is a convention. It is chosen to match the convention used in defining the counterclockwise orientation of a curve in Green's theorem, ensuring consistency in calculations.
What is a limitation of Green's theorem mentioned in the script?
-A limitation of Green's theorem is that it can only be applied to closed curves. If a curve is not closed, the line integral must be computed by parameterizing the curve or by closing the path and then applying the theorem.
How does the script simplify the proof of Green's theorem?
-The script simplifies the proof by first proving the theorem for the case where there is only an x-component of the vector field and the region is vertically simple. Then, it extends the proof to more complex regions by decomposing them into simpler regions and using the principle of superposition.
What is a planimeter and how was it historically used?
-A planimeter is a device historically used to measure areas, especially those that are irregular or complex. It computes a line integral along the boundary of the region of interest, and by applying Green's theorem, it provides the area of the region.
What is the modern alternative to using a planimeter for measuring areas?
-The modern alternative to using a planimeter is to use a computer to sum up the areas of small squares or to perform numerical integration, which is more efficient and precise.
Outlines
📚 Introduction to Green's Theorem and Conservative Vector Fields
This paragraph introduces the concept of Green's theorem in the context of vector calculus, specifically for computing line integrals along closed curves. It discusses the curl of a vector field, which measures its deviation from being conservative. If the curl is zero everywhere, the field is conservative, and the line integral over any closed path will be zero. The paragraph also introduces the two methods of calculating line integrals: direct computation and using Green's theorem, which is applicable when the vector field is defined and differentiable everywhere, including inside the enclosed region.
🔍 Exploring Green's Theorem with an Example
The speaker provides a practical example to illustrate the application of Green's theorem. They describe a scenario where a line integral over a circle is to be calculated using the theorem, avoiding the direct computation method. The example involves a circle with a specific radius and center, and a vector field with components that, when applied through Green's theorem, simplify the calculation significantly. The explanation includes a brief discussion on parameterization and the transformation of a line integral into a double integral.
📘 Simplifying Complex Line Integrals Using Green's Theorem
This section delves deeper into the simplification of complex line integrals through the application of Green's theorem. It explains how the theorem can transform a challenging line integral into a more manageable double integral. The speaker provides a method to compute the double integral by relating it to the geometric center of mass of the region, offering a clever way to avoid direct integration and instead use symmetry and geometric properties to find the result.
🤔 The Validity of Green's Theorem and Conservative Vector Fields
The speaker discusses the conditions under which Green's theorem and the concept of conservative vector fields hold true. They highlight the importance of the curl being zero for a vector field to be conservative and emphasize that this must be true everywhere in the plane. The paragraph also addresses the limitations of Green's theorem, noting that it cannot be applied to non-closed curves or vector fields that are not defined everywhere, such as those with singularities at certain points.
🔧 A Counterexample and the Limitations of Green's Theorem
The paragraph presents a counterexample to demonstrate the limitations of Green's theorem. It describes a vector field with zero curl everywhere except at the origin, where it is undefined. This example shows that even if a vector field has zero curl, it may not be conservative if it is not defined over the entire plane. The discussion also touches on the implications of the vector field not being defined at a point, which affects the applicability of Green's theorem.
📐 Proving Green's Theorem Step by Step
This section outlines the process of proving Green's theorem. The speaker breaks down the proof into simpler cases, starting with scenarios where the vector field has only an x-component and the region is vertically simple. The explanation involves setting up line integrals for each part of the boundary and comparing them to the double integral over the region. The paragraph also discusses the strategy of decomposing a complex region into simpler ones to facilitate the proof.
🛠️ Completing the Proof of Green's Theorem
The speaker completes the proof of Green's theorem by considering the case of a vertically simple region and then generalizing it to any region. They demonstrate how the line integral along the boundary of the region is equivalent to the double integral over the region, leading to the conclusion of the theorem. The explanation includes the process of integrating over the boundary segments and summing these integrals to match the double integral.
📡 A Historical Application of Green's Theorem: The Planimeter
The final paragraph discusses a historical application of Green's theorem in the form of a device called a planimeter, which was used to measure areas under curves on graph paper. The speaker explains how the planimeter works by computing a line integral along the curve, which, according to Green's theorem, equates to the area of the region enclosed by the curve. The paragraph reflects on the obsolescence of such devices due to modern computing technology.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Vector field
💡Curl
💡Conservative vector field
💡Line integral
💡Green's theorem
💡Double integral
💡Parameterize
💡Center of mass
💡Planimeter
Highlights
Introduction to the concept of curl in vector fields and its role in determining if a field is conservative.
Explanation of how a zero curl value implies a conservative vector field and the implications for line integrals over closed curves.
The presentation of Green's theorem as an alternative method for calculating line integrals without direct computation.
Conditions for applying Green's theorem, including the requirement for the curve to be closed and the vector field to be differentiable within the enclosed region.
A step-by-step guide on how to use Green's theorem to convert a line integral into a double integral.
The significance of the direction of the curve (counterclockwise) in applying Green's theorem and the convention behind it.
An example of calculating the line integral of a vector field over a circle using Green's theorem instead of direct parameterization.
A demonstration of simplifying complex line integrals into more manageable double integrals using Green's theorem.
The geometric interpretation of the double integral as the area of a region times the x-coordinate of its center of mass.
A discussion on the limitations of Green's theorem, particularly its application to non-closed curves.
An exploration of the special case where the curl of a vector field is zero and the implications for proving the field's conservative nature.
A detailed proof of Green's theorem using vertically simple regions and the decomposition of complex regions into simpler ones.
The mathematical process of proving Green's theorem by equating the line integral to the double integral over a simplified region.
The historical application of Green's theorem in the use of planimeters for measuring areas on graph paper.
The demonstration of how a planimeter works by computing a line integral that corresponds to the area inside a curve via Green's theorem.
A reflection on the obsolescence of planimeters due to modern computing technology.
Transcripts
Browse More Related Video

Calculus 3: Green's Theorem (Video #30) | Math with Professor V
Green's Theorem

Green's Theorem, explained visually

Lec 24: Simply connected regions; review | MIT 18.02 Multivariable Calculus, Fall 2007

Calculus Chapter 3 Lecture 26 The FTIC

Lec 20: Path independence and conservative fields | MIT 18.02 Multivariable Calculus, Fall 2007
5.0 / 5 (0 votes)
Thanks for rating: