Fun Math Videos!

This paragraph introduces the concept of fractions using the relatable example of sharing a pizza. It explains that a fraction represents parts of a whole, using the scenario of Cindy and Chomsky dividing a pizza to illustrate one-half. The explanation includes the definition of numerators and denominators, emphasizing that the denominator shows the total parts and the numerator shows the parts being considered. The paragraph aims to demystify fractions and present them as a fundamental and commonly used mathematical concept.

Building upon the basic understanding of fractions, this paragraph explores how to determine what fraction of a group is represented by a subset, using sports balls as an example. It outlines the process of identifying the total number of items (the denominator) and the number of items in the subset of interest (the numerator). The paragraph reinforces the concept of fractions by showing how they can be used to describe parts of a collection, such as one-fifth being basketballs out of five sports balls.

This paragraph continues the theme of fractions with a different example, determining what fraction of a group of pets are cats. It also introduces Roman numerals as an ancient method of representing numbers, explaining the basic symbols for one (I), five (V), and ten (X). The paragraph serves to further familiarize viewers with fractions and offers an introduction to the historical context of Roman numerals, adding a cultural element to the mathematical lesson.

Using the story of Ethan and his friends sharing carrots, this paragraph teaches the concept of division. It simplifies division as the act of splitting a number evenly among a certain quantity. The paragraph explains how to perform division with the example of three carrots shared among three kids, resulting in one carrot per child. It emphasizes the idea that division is about fairness and equal distribution, and introduces the division sign, highlighting that division by zero is undefined.

This paragraph delves into interesting facts about division, such as the impossibility of dividing by zero and the various ways to represent the division operation, including the traditional division sign, a slash, and a horizontal line. It also introduces the concept that the order of the divisor and dividend can be switched without changing the outcome of the division, providing a deeper understanding of division's properties and its mathematical notation.

The paragraph introduces the distinction between even and odd numbers using a playful detective theme with dinosaurs. It explains that even numbers can be grouped into pairs, while odd numbers have one left over. The summary includes the identification of even and odd numbers through examples with dinosaurs and mentions two tricks: the alternation pattern of odd and even numbers, and the rule that the last digit of a number determines its parity, with even numbers ending in 0, 2, 4, 6, or 8.

This paragraph presents multiplication as a fun detective game where one must figure out the total number of items in several groups. It explains the basic concept of multiplication as adding the same number several times, using the examples of bicycles with tires and packs of trading cards. The paragraph simplifies multiplication as a process of adding a number to itself as many times as indicated by another number, emphasizing the importance of understanding the number of groups and the number within each group.

Building on the multiplication concept, this paragraph shares tricks to simplify multiplication problems, such as the outcomes of multiplying by zero or one, and the use of multiplication tables. It emphasizes that multiplying by zero always results in zero, while multiplying by one leaves the number unchanged. The paragraph also highlights the utility of multiplication tables in quickly solving common multiplication problems, making the learning process more accessible and efficient.

This paragraph introduces the concept of perimeter through the analogy of a race car track, explaining that the perimeter is the distance around a shape. It provides examples of calculating the perimeter for different shapes, such as a triangle, a square, and a rectangle, by adding the lengths of their sides. The summary illustrates the process of finding the perimeter and emphasizes its importance in understanding the dimensions of two-dimensional spaces.

The paragraph transitions from 2D to 3D shapes, starting with a review of familiar 2D shapes like the circle, oval, triangle, and square, and then introducing the concept of three-dimensional shapes. It explains that 3D shapes are 'fat not flat' and provides the sphere as the first example of a 3D shape, comparing it to its 2D counterpart, the circle. The summary sets the stage for a deeper exploration of 3D shapes and their characteristics, highlighting the transition from flat shapes to those with depth.

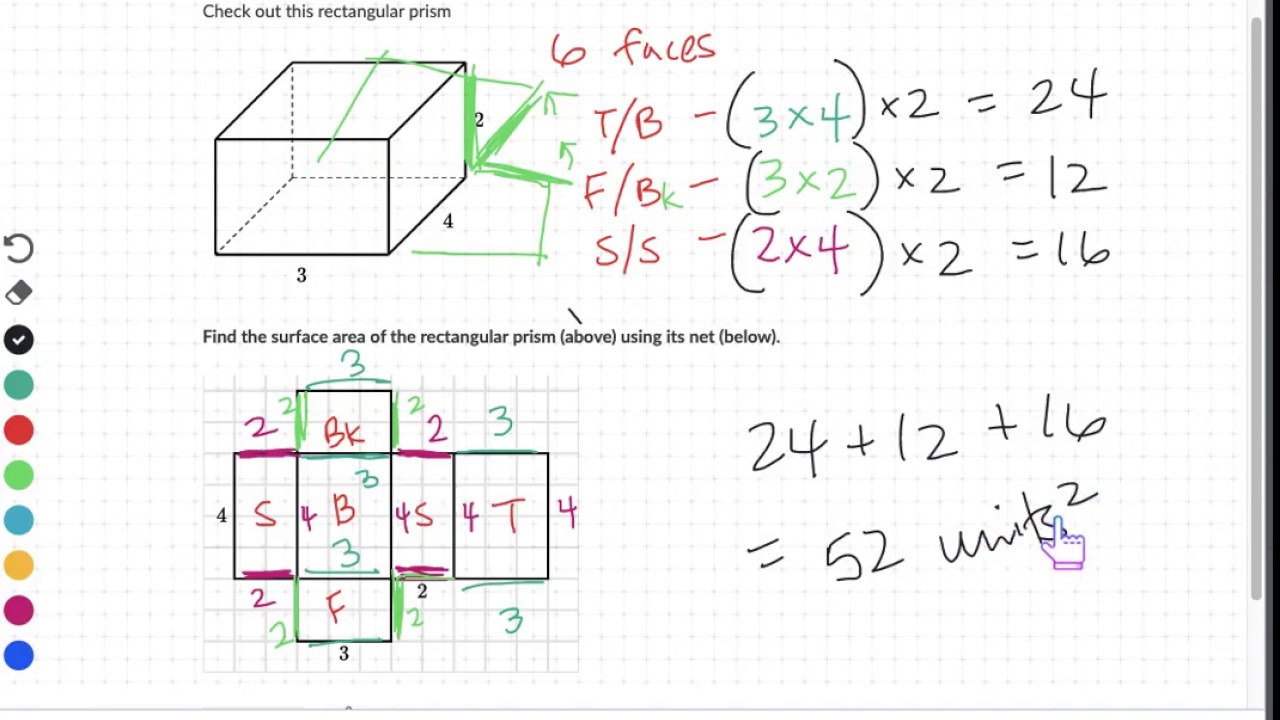
This paragraph takes the viewer on a journey through various three-dimensional shapes, starting with the sphere and moving on to the cone, pyramid, cylinder, cube, and rectangular prism. Each shape is described with its distinctive features, such as the sphere being perfectly round with no flat surfaces, the cone having a circular base and a single vertex, and the rectangular prism being the 3D version of a rectangle with six rectangular faces. The summary provides examples of where these shapes can be found in everyday life, emphasizing their prevalence and utility.

The paragraph concludes the lesson on 3D shapes with a celebration of the learner's achievements and a review of the shapes covered. It uses visual aids to help identify and remember the characteristics of each 3D shape, from the sphere to the rectangular prism. The summary highlights the importance of recognizing and differentiating between these shapes, encouraging continued learning and exploration of the three-dimensional world.