Calculus BC – 10.5 Harmonic Series and p-series
TLDRIn this calculus lesson, Mr. Bean introduces p-series, a type of infinite series characterized by a positive constant exponent p. He explains that if p is greater than one, the series converges; if p is between zero and one, it diverges. The harmonic series, a special case of p-series with p=1, is also discussed and noted to always diverge. The lesson emphasizes the importance of distinguishing between p-series and geometric series, where the latter converges if the common ratio is less than one. Practice problems are provided to solidify understanding, and the video concludes with a review of various series tests.
Takeaways
- 📚 The lesson focuses on 'p-series' in calculus, a type of series where the denominator has a power of the numerator, n, raised to a positive constant p.
- 🔍 The convergence of a p-series is determined by the value of p: if p > 1, the series converges; if 0 < p ≤ 1, it diverges.
- 🔑 A special case of p-series is the harmonic series, where the exponent p is 1, and it is known to diverge.
- 🤔 The teacher emphasizes the difference in convergence criteria between p-series and geometric series, where in the latter, a common ratio r < 1 leads to convergence.
- 📝 To determine if a series is a p-series, the base of the exponent must be n, and the exponent itself determines convergence or divergence.
- 📉 The teacher provides a method to remember convergence: if the exponent is a large number, the series approaches 1/infinity, which is zero and thus converges.
- 📌 Practice problems are used to illustrate how to identify and determine the convergence or divergence of p-series, including cases where the value of p is variable.
- 🧩 The script distinguishes between p-series and geometric series, noting that the position of the variable in the exponent is key to identifying the series type.
- 🔢 The teacher explains how to solve for the value of k in a series to determine its convergence by setting the exponent greater than one and solving for k.
- ✂️ For more complex series expressions, the teacher suggests factoring out n to simplify the expression and identify the p value for convergence assessment.
- 🔄 The lesson includes a quick review of other series tests such as the geometric series test, nth term test for divergence, and the integral test, highlighting their differences from the p-series criteria.
Q & A
What is the main focus of the lesson presented by Mr. Bean?
-The main focus of the lesson is on p-series, with a brief introduction to harmonic series.
What is a p-series in calculus?
-A p-series is an infinite series of the form \(1 + \frac{1}{n^p} + \frac{1}{(n+1)^p} + \frac{1}{(n+2)^p} + \ldots\), where \( p \) is a positive constant in the denominator.
How can you determine if a p-series is converging or diverging?
-A p-series converges if the value of \( p \) is larger than one, and it diverges if the value of \( p \) is between zero and one.
What is the difference between a p-series and a geometric series?
-In a p-series, the exponent \( p \) is a positive constant, and the series converges if \( p > 1 \) and diverges if \( 0 < p \leq 1 \). In a geometric series, the common ratio \( r \) determines convergence, where it converges if \( |r| < 1 \) and diverges if \( |r| \geq 1 \).
What is a harmonic series?
-A harmonic series is a special type of p-series where the exponent \( p \) is equal to 1, resulting in the series \( 1 + \frac{1}{2} + \frac{1}{3} + \ldots\), which is known to diverge.
How does the convergence of a p-series compare to the nth term test for divergence?
-The nth term test for divergence states that if the limit of \( a_n \) as \( n \) approaches infinity is not zero, then the series diverges. For a p-series, the series diverges if \( 0 < p \leq 1 \) and converges if \( p > 1 \), which is the opposite direction of the nth term test for convergence.
What is the significance of the value of p being greater than one in a p-series?
-If the value of \( p \) is greater than one in a p-series, it indicates that the series is converging. This is a key factor in determining the convergence of a p-series.
Can you provide an example of a p-series that converges?
-An example of a converging p-series is \( 1 + \frac{1}{2^3} + \frac{1}{3^3} + \ldots\), where \( p = 3 \) and since \( p > 1 \), the series converges.
How does the lesson differentiate between p-series and geometric series?
-The lesson differentiates by explaining that in a p-series, the base is \( n \) and the exponent determines convergence or divergence, whereas in a geometric series, the common ratio \( r \) determines convergence or divergence.
What is the relationship between the value of k and the convergence of a series in the form \( n^{2k-5} \)?
-For the series \( n^{2k-5} \) to converge, the value of \( k \) must be greater than 3, as \( 2k - 5 > 1 \) when \( k > 3 \).
How does the lesson illustrate the manipulation of a series to identify it as a p-series?
-The lesson shows that by factoring out an \( n \) and rewriting the series, you can identify the exponent \( p \) and determine if the series is a p-series and whether it converges or diverges.
Outlines
📚 Introduction to P-Series and Harmonic Series
In this calculus lesson, Mr. Bean introduces the concept of P-series, which are series where the denominator is raised to a positive constant exponent (p). He explains that if p is greater than one, the series converges, but if p is between zero and one, the series diverges. The lesson also touches on the harmonic series, a special case of P-series where the exponent is one. The harmonic series is known to diverge. Mr. Bean emphasizes the importance of recognizing the difference between P-series and geometric series, where the convergence or divergence depends on the ratio (r) being less than one or greater than one, respectively.
🔍 Analyzing Convergence in P-Series
This paragraph delves deeper into the specifics of determining whether a series is a P-series and its convergence. Mr. Bean provides examples and explains the process of identifying the value of p in a series. He clarifies that recognizing the series as a P-series is the first step, followed by determining the value of p to decide if the series converges or diverges. The paragraph also discusses how to handle series where the exponent is not immediately obvious, such as when it is expressed as a function of another variable (e.g., 2k - 5). The key takeaway is that the series converges if the exponent is greater than one, and diverges otherwise. Mr. Bean also reviews other series tests like the geometric series test, nth term test, and integral test, highlighting the differences in their criteria for convergence and divergence.
Mindmap
Keywords
💡Calculus
💡p-series
💡Convergence
💡Divergence
💡Harmonic Series
💡Exponent
💡Geometric Series
💡nth Term Test
💡Integral Test
💡Practice Problems
💡Manipulation
Highlights
Introduction to p-series and its importance in calculus.
Definition of p-series: a series where the exponent p is a positive constant in the denominator.
Explanation of convergence: If p is larger than 1, the series converges.
Explanation of divergence: If p is between 0 and 1, the series diverges.
Clarification that p cannot be less than 0 as it would change the nature of the series.
Introduction to harmonic series: a special type of p-series where the exponent is 1.
Key point: Harmonic series diverge.
Practice example to identify if a series converges or diverges by recognizing it as a p-series.
Distinction between p-series and geometric series.
Explanation of geometric series: convergence depends on the common ratio being less than 1.
Step-by-step example: determining the value of k for which a series converges.
Method for simplifying complex expressions to identify the exponent p.
Summary of p-series rules: converging if p > 1, diverging if 0 < p < 1.
Quick review of geometric series and the importance of the common ratio in determining convergence.
Review of nth term test: if the limit of a term as n approaches infinity is not zero, the series diverges.
Reminder of integral test: using integrals to determine if a series converges or diverges.
Transcripts
Browse More Related Video

AP Calculus BC Lesson 10.5

Proof of p-series convergence criteria | Series | AP Calculus BC | Khan Academy
Calculus Chapter 5 Lecture 52 Convergence Tests 2

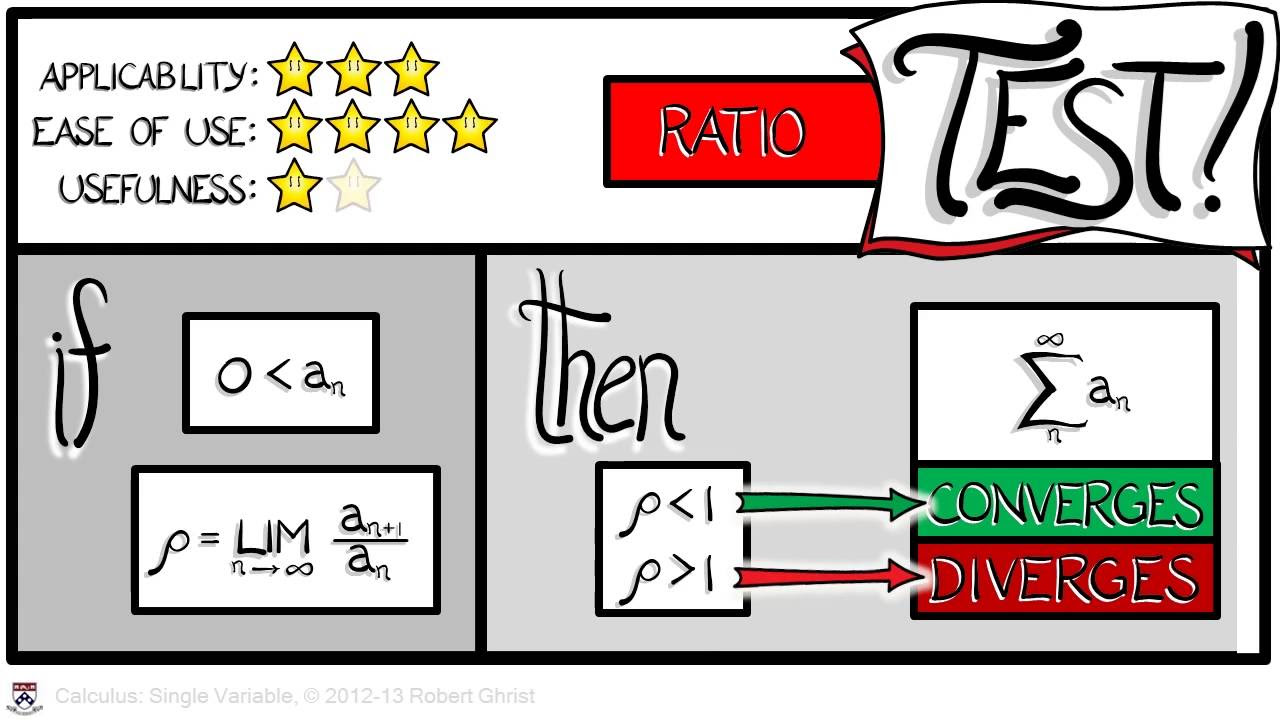
Calculus BC – 10.8 Ratio Test for Convergence
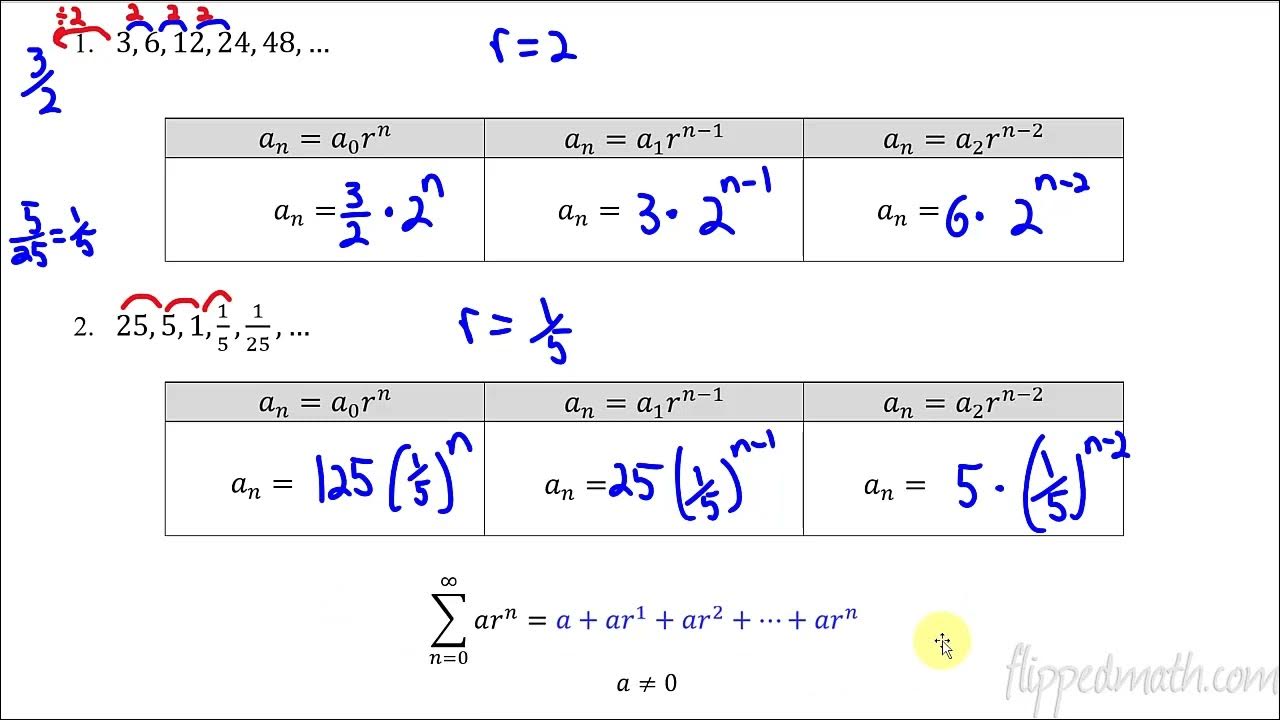
Calculus BC – 10.2 Working with Geometric Series

Direct comparison test | Series | AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: