Justifying Our Answers in AP Calculus
TLDRThis video discusses strategies for justifying answers in calculus AB free response questions. It covers identifying relative extrema using the first and second derivative tests, finding absolute extrema on closed intervals, applying L'Hôpital's rule, solving equations with technology, and understanding points of inflection. The emphasis is on clear justifications and proper use of calculus concepts.
Takeaways
- 📚 The video discusses justifying answers on free response questions for Calculus AB, focusing on concepts like relative extrema, first and second derivative tests, and L'Hôpital's Rule.
- 📈 A relative extremum is a point where there is a sign change in the first derivative. The first derivative test is used to determine the nature of this sign change.
- 🔍 When identifying relative extrema, it's crucial to be explicit about the derivative of the function and how it changes from negative to positive or vice versa.
- 📉 The second derivative test is useful for determining if a point is a maximum, minimum, or neither, especially when the first derivative is zero. It involves checking if the second derivative is positive (indicating a minimum) or negative (indicating a maximum).
- 🏁 The video emphasizes the importance of being explicit in stating that the first derivative equals zero and the sign of the second derivative when using the second derivative test.
- 🔢 For absolute extrema, the closed interval test involves evaluating the function at endpoints and critical points to determine the maximum or minimum value on a closed interval.
- 📌 When using L'Hôpital's Rule, it's essential not to equate the limit to '0/0' and to maintain proper limit notation. The rule applies when both the numerator and denominator approach zero or infinity.
- 📊 In calculator-active scenarios, students must be able to solve equations, take derivatives, and integrate functions. Graphing is only for perspective and not part of the answer.
- 🧩 Separation of variables in differential equations involves moving all y terms to one side and all x terms to the other, then integrating both sides to find the particular solution.
- 📐 Points of inflection are identified by sign changes in the second derivative. It's important to justify answers by discussing the change in signs rather than just stating the second derivative equals zero.
Q & A
What is a relative extremum in calculus?
-A relative extremum, which includes relative maximums and minimums, is a point on the graph of a function where there is a sign change in the first derivative.
What is the first derivative test used for in calculus?
-The first derivative test is used to determine the nature of extreme points, such as relative maxima and minima, by examining the sign changes of the first derivative around those points.
How can you justify the answer for a relative extremum on an AP exam?
-On an AP exam, you should justify the answer for a relative extremum by explicitly stating the x-value, noting that the first derivative changes sign at that point, and providing the derivative function that exhibits the sign change.
What is the second derivative test and when is it best used?
-The second derivative test is used to determine the concavity of a function at a point where the first derivative is zero. It is best used when the first derivative is zero and the second derivative can indicate whether the function has a local minimum or maximum at that point.
Why is it important to check that the first derivative equals zero before using the second derivative test?
-It is important to check that the first derivative equals zero because if it does not, the function is in the midst of increasing or decreasing and could not be at an extreme. The second derivative test is only applicable when the first derivative is zero.
What is L'Hôpital's rule and when should it be used?
-L'Hôpital's rule is a method for finding the limit of a function as x approaches a certain value, particularly when the limit results in an indeterminate form like 0/0 or ∞/∞. It states that the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives.
How should you approach solving a calculus problem involving a horizontal tangent using a calculator?
-To solve for a horizontal tangent using a calculator, you should set the derivative of the function equal to zero and use the calculator to find the x-values where this equation holds true within a specified interval.
What is the importance of justifying the steps taken when using a calculator in a calculus problem?
-Justifying the steps taken when using a calculator is important to show the reader of your work that you have correctly applied the mathematical principles and calculator functions to arrive at your solution.
What is a point of inflection and how can you determine it?
-A point of inflection is a point on the graph of a function where the concavity changes. It can be determined by finding where the second derivative of the function changes sign.
Why is it incorrect to say that a point is a point of inflection just because the second derivative is zero?
-It is incorrect because a point of inflection is characterized by a sign change in the second derivative, not just the second derivative being zero. There can be points where the second derivative is zero but the function does not change concavity.
What is the significance of the initial condition in solving a differential equation?
-The initial condition is crucial in solving a differential equation as it provides the specific value of the function or its derivative at a given point, which allows you to determine the constant of integration (C) and find the particular solution.
How should you handle the 'plus C' when anti-differentiating in a calculus problem?
-You should include the 'plus C' immediately after anti-differentiating, not waiting until a later step. This ensures that you account for the constant of integration and that it is in the correct place in your solution.
Outlines
📚 Justifying Answers in Calculus: Relative Extrema and the First Derivative Test
This paragraph introduces the concept of relative extrema in calculus and the importance of justifying answers on free response questions. It explains the first derivative test, which involves identifying sign changes in the first derivative of a function. The instructor emphasizes the need to be explicit about the nature of the sign change and provides an example with a function g, where the derivative g' is f(x), and how to identify a minimum at x=2 by showing g' goes from negative to positive. The paragraph also touches on the importance of being able to justify answers for algebraically defined functions, using an example of a cubic polynomial and the process of finding its relative maximum by taking the derivative and setting it to zero, factoring, and using a sign chart to determine where the sign change occurs.
📐 Understanding the Second Derivative Test and Absolute Extrema
The second paragraph delves into the second derivative test, which is used to determine the nature of critical points when the first derivative is zero. It stresses the importance of verifying that the first derivative is indeed zero before applying the second derivative test. The instructor uses an example involving implicit differentiation to find where the second derivative is negative, indicating a maximum. The paragraph also discusses the concept of absolute extrema on a closed interval, explaining the closed interval test and how to evaluate the function at endpoints and critical points to find the maximum value. The need to justify the selection of critical points and the process of evaluating the function at these points is highlighted, along with the importance of providing a clear justification for each step.
📈 L'Hôpital's Rule and Its Proper Application in Limits
This paragraph discusses L'Hôpital's rule, which is used to evaluate limits of the form 0/0 or ∞/∞ by taking the limit of the ratio of their derivatives. The instructor cautions against incorrectly stating '0 over 0' and emphasizes maintaining proper limit notation. An example is provided where the rule is applied to a function involving an integral and a differentiable function f, with specific values for f(4) and f'(4). The process involves recognizing that both the numerator and denominator approach zero, applying L'Hôpital's rule, and then calculating the limit of the ratio of their derivatives to find the value of the original limit.
🔍 Calculator Active Scenarios: Solving Equations and Justifying Answers
The fourth paragraph focuses on the use of calculators in solving equations and emphasizes the importance of justifying each step in a calculator-active scenario. The instructor provides a step-by-step guide on how to set up and solve an equation using a calculator, using the example of finding the x-coordinate where a function has a horizontal tangent. The paragraph also covers how to take derivatives and integrals using a calculator, with an example of finding acceleration at a specific time and calculating total distance. The importance of explaining the process and the calculator inputs to justify the answers is highlighted.
📝 Separation of Variables and Initial Conditions in Differential Equations
The fifth paragraph discusses the technique of separation of variables in solving differential equations, with an example that includes an initial condition. The process involves moving all terms involving y to one side and all terms involving x to the other, integrating both sides, and then solving for y. The instructor explains how to anti-differentiate, handle the constant of integration, and use the initial condition to find the particular solution. The importance of showing each step and the reasoning behind it is emphasized, along with the scoring guidelines for such problems.
🔄 Points of Inflection: Identifying and Justifying Inflection Points
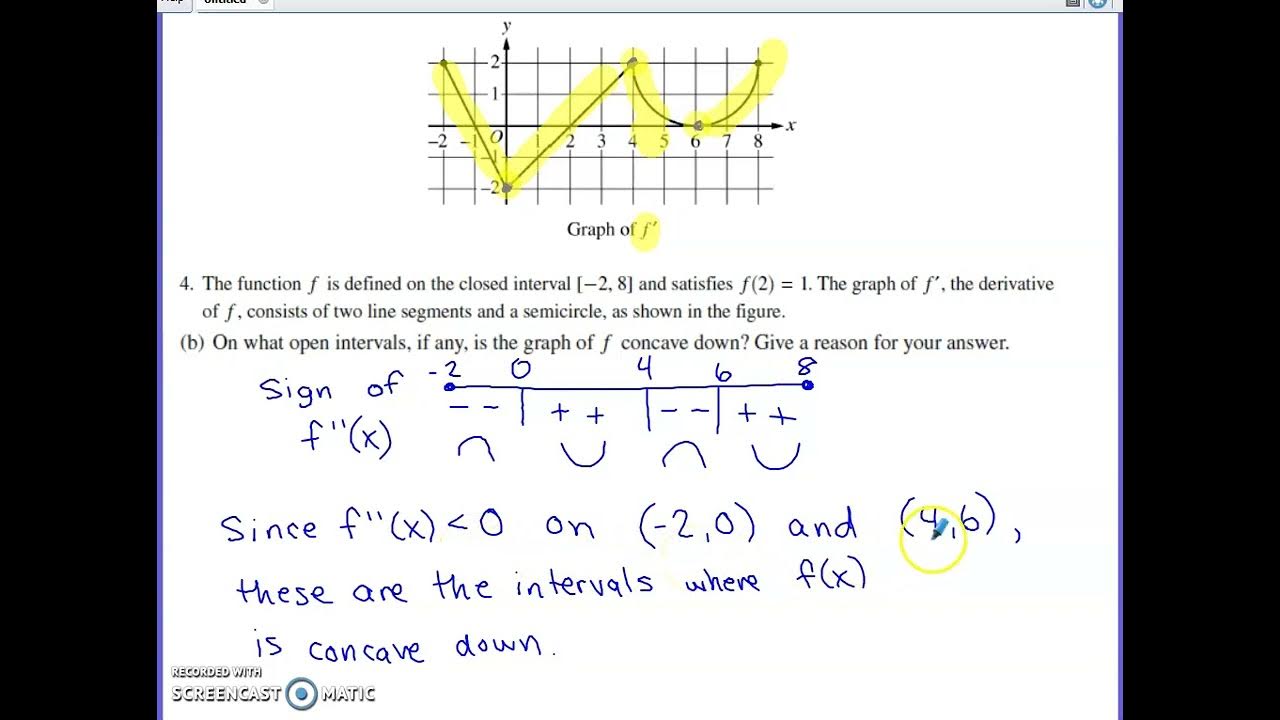
The sixth paragraph addresses the concept of points of inflection, which are identified by sign changes in the second derivative of a function. The instructor explains how to find these points by computing the second derivative and then determining where it changes signs. Examples are provided, including a polynomial and a function with an exponential term, to illustrate how to create a sign chart or sketch the second derivative to find the inflection points. The paragraph emphasizes the need to justify the identification of inflection points based on sign changes rather than simply stating that the second derivative is zero.
📉 Inflection Points in Functions: Graphical and Algebraic Analysis
The final paragraph continues the discussion on inflection points, providing a more detailed analysis of how to determine them both graphically and algebraically. The instructor demonstrates how to create a sign chart for a function with an exponential term and how to sketch the graph of a polynomial to identify inflection points. The importance of declaring the inflection points based on the change in sign of the second derivative is stressed, and the instructor clarifies that stating the second derivative equals zero is not sufficient for justification. The paragraph concludes with a summary of the key points covered in the video script in preparation for an upcoming exam.
Mindmap
Keywords
💡Relative Extrema
💡First Derivative Test
💡Algebraically Defined Functions
💡Second Derivative Test
💡L'Hôpital's Rule
💡Absolute Extrema
💡Separation of Variables
💡Point of Inflection
💡Sign Chart
💡Calculator Active Scenario
Highlights
Discussing the justification of answers in calculus, focusing on relative extrema.
A relative extremum is a point where there's a sign change in the first derivative.
The first derivative test is used to determine the nature of a sign change.
Graphical interpretation of minimum points on a graph is discussed.
Emphasis on the importance of explicitly stating the derivative of a function.
Explanation of how to use the first derivative test for algebraically defined functions.
Demonstration of finding relative maxima using a third-degree polynomial example.
Clarification on the necessity of factoring to find sign changes in derivatives.
Introduction of the second derivative test and its appropriate use cases.
Highlighting the need to explicitly state that the first derivative is zero before using the second derivative test.
Discussion on absolute extrema and the closed interval test.
Explanation of evaluating function values at endpoints and critical points for absolute extrema.
Mention of L'Hôpital's rule and its correct application in calculus.
Emphasis on avoiding the phrase 'equals zero over zero' when using L'Hôpital's rule.
Guidance on solving equations, taking derivatives, and integrals in a calculator-active scenario.
Description of the process for solving an equation using technology and the importance of describing the equation.
Explanation of how to take a derivative and integral using a calculator and the need for justification.
Review of separation of variables in differential equations and the importance of showing work.
Discussion on finding points of inflection and the significance of sign changes in the second derivative.
Clarification that points of inflection are determined by sign changes, not just where the second derivative is zero.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: