The Second Fundamental Theorem of Calculus
TLDRThis video tutorial delves into the Second Fundamental Theorem of Calculus, which explains how to differentiate a function defined by an integral. The instructor provides examples to illustrate the process, including handling integrals with variable bounds and using dummy variables to avoid circular dependencies. The video also covers applications of the theorem, such as finding derivatives of functions, analyzing the slope of tangent lines, and solving L'Hôpital's rule problems. The content is geared towards AP Calculus students, offering practical insights and strategies for tackling related exam questions.
Takeaways
- 📚 The Second Fundamental Theorem of Calculus explains how to find the derivative of a function defined by an integral.
- 🔍 The theorem shows a relationship between the derivative of a function and the integrand of the integral that defines it.
- 🌐 The integral can be thought of as an area-counting function, and the derivative of this function is the integrand itself.
- 📉 The video provides an example using the integral of cosine of t from zero to x, demonstrating how the derivative of the function g(x) is cos(x).
- 🧩 The concept of a dummy variable (like t) is introduced to avoid confusion when the variable of integration is also the variable of differentiation.
- 🔄 The video discusses how to handle integrals where both the upper and lower bounds of integration are functions of x, using the chain rule and product rule.
- 📈 The script includes an example of finding the second derivative of a function defined by an integral, illustrating the use of the product rule.
- 📚 The video explains how to deal with situations where the bounds of integration are more complex, such as when they are functions of x.
- 📉 The script discusses the implications of the Second Fundamental Theorem for finding tangent lines, maximum and minimum values, and points of inflection.
- 🏔 The video connects the theorem to real-world applications, such as analyzing graphs and determining properties like slopes of tangent lines and areas under curves.
- 🏁 The script concludes with an example involving L'Hôpital's Rule, demonstrating how to handle limits that approach zero over zero using the newly learned derivative rules.
Q & A
What is the first fundamental theorem of calculus?
-The first fundamental theorem of calculus establishes a relationship between the area problem and the anti-derivative problem. It states that the area under a curve can be found by computing the net change in its anti-derivative.
What does the second fundamental theorem of calculus tell us?
-The second fundamental theorem of calculus tells us how to take the derivative of a function defined by an integral. It allows us to find the derivative of an area counting function for the area under the graph of some function 'f' between 'x=a' and some other 'x' value.
Why is the variable 't' used in integrals?
-The variable 't' is used as a dummy variable in integrals to avoid confusion and potential circular dependencies when the variable of integration is the same as the variable with respect to which we are differentiating.
What is the significance of the zero in the lower bound of integration?
-The zero in the lower bound of integration is significant because it simplifies the computation of the derivative of the integral. It does not contribute to the derivative of the function 'g', as it represents a constant that is subtracted from the anti-derivative evaluated at 'x'.
How can the second derivative of a function defined by an integral be found?
-The second derivative of a function defined by an integral can be found by first applying the second fundamental theorem to find the first derivative, and then differentiating that result, often using derivative rules such as the product rule or chain rule.
What happens if the upper bound of integration is a function of 'x'?
-If the upper bound of integration is a function of 'x', the second fundamental theorem can still be applied. The 'x' in the function is substituted for 't' in the integrand, and the derivative of the function (with respect to 'x') is multiplied by the integrand due to the chain rule.
How is the derivative of a function with a variable lower bound of integration handled?
-When the lower bound of integration is variable with respect to 'x', the derivative is found by substituting 'x' for the dummy variable in the integrand and then multiplying by the negative of the derivative of the lower bound of integration, due to the reverse in the bounds of integration.
What is the equation for a tangent line in the context of this script?
-The equation for a tangent line is derived from a point on the curve and the slope of the tangent at that point. The slope is found by differentiating the function defined by an integral, and the equation is in the form 'y - y-coordinate = slope * (x - x-coordinate)'.
How can the second fundamental theorem be applied when both bounds of integration are variable with respect to 'x'?
-When both bounds of integration are variable with respect to 'x', the second fundamental theorem is applied by substituting the upper and lower bounds into the integrand and then multiplying by their respective derivatives due to the chain rule. The derivative of the function is the difference of these two results.
What is an example of a scenario where the second fundamental theorem is applied in an AP Calculus exam?
-An example scenario in an AP Calculus exam might involve a graph of a function and questions about its antiderivative. The second fundamental theorem is applied to find values, derivatives, and analyze the behavior of the function, such as finding points of inflection, maximum and minimum values, and applying L'Hôpital's rule for indeterminate forms.
Outlines
📚 Introduction to the Second Fundamental Theorem of Calculus
This paragraph introduces the second fundamental theorem of calculus, which explains how to find the derivative of a function defined by an integral. It serves as a reminder of the first fundamental theorem, which relates the area under a curve to the anti-derivative, and then delves into how the second theorem allows us to differentiate an integral function. The speaker provides examples, including the integral of cosine of t from 0 to x, to demonstrate the process and the use of dummy variables, t, in the integral. The importance of the constant nature of the lower bound of integration is highlighted, and the paragraph concludes with the understanding that the derivative of a function defined by an integral is the integrand itself.
🔍 Derivatives of Functions Defined by Integrals with Variable Bounds
The speaker explores the scenario where the upper bound of integration is not simply x but a function of x, and how to handle this using the second fundamental theorem. The example of the integral of cosine of x squared from 5 to x is used to illustrate the process, with emphasis on the chain rule and the importance of differentiating the outer function of a composite function. The paragraph also addresses the situation where the lower bound of integration is variable, explaining that it results in a negative derivative due to the reversal of integration bounds. The concept of the tangent line equation is introduced, with an example of finding the slope and point of tangency for a given function.
📉 Handling Complex Derivatives with Both Variable Bounds of Integration
This paragraph discusses a more complex scenario where both the upper and lower bounds of integration are variables with respect to x. The speaker presents a unified approach to finding the derivative in such cases, which involves applying the second fundamental theorem to both bounds and using the chain rule. An example of a function defined by an integral with both bounds as functions of x is provided, and the process of finding its derivative is demonstrated. The paragraph emphasizes the importance of understanding the role of each bound and how they contribute to the derivative of the function.
📈 Applications of the Second Fundamental Theorem in AP Calculus
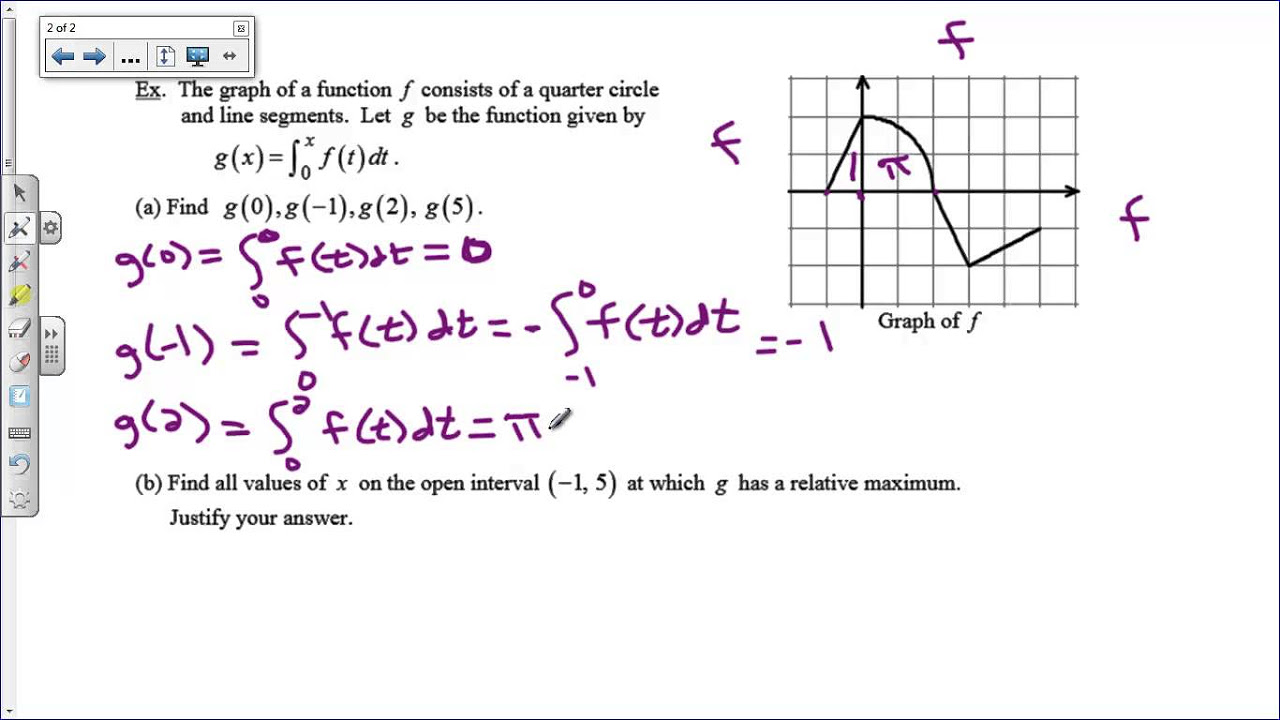
The speaker connects the theoretical discussion to practical applications, specifically in the context of AP Calculus exams. The paragraph covers how to find values of a function defined by an integral, the significance of acknowledging that the derivative of such a function is the integrand itself, and how to identify points of inflection and extrema. The speaker also discusses how to find the absolute minimum value of a function on a closed interval, using both critical points and endpoints for consideration.
📌 Solving L'Hôpital's Rule Problems Using the Second Fundamental Theorem
The final paragraph addresses a specific application of the second fundamental theorem in conjunction with L'Hôpital's rule. The speaker presents a limit problem that results in an indeterminate form of 0/0 and demonstrates how to resolve it by taking derivatives, as per L'Hôpital's rule. The example involves the integral from 5 to x of the cube root of t, which simplifies to a straightforward calculation once the derivatives are applied. The paragraph concludes with a reference to further examples in a solutions video for additional practice.
Mindmap
Keywords
💡Second Fundamental Theorem of Calculus
💡Anti-derivative
💡Derivative
💡Integral
💡Dummy Variable
💡Area Function
💡Chain Rule
💡L'Hôpital's Rule
💡Tangent Line
💡Concave Up/Down
💡Relative Extrema
💡Absolute Minimum/Maximum
Highlights
Introduction to the Second Fundamental Theorem of Calculus, which explains how to take the derivative of a function defined by an integral.
The First Fundamental Theorem of Calculus is a reminder that the area under a curve can be found by computing the net change in its anti-derivative.
Demonstration of the Second Fundamental Theorem by showing the derivative of an integral is the integrand itself.
Explanation of the importance of using a dummy variable in integrals to avoid circular dependency.
Example calculation of the derivative of an integral from zero to x of cosine(t)dt, illustrating the theorem in action.
Clarification on why the lower bound of integration does not affect the derivative of the function defined by the integral.
The use of the chain rule in finding the second derivative of a function defined by an integral.
Application of the Second Fundamental Theorem in solving derivative-related problems such as slope of tangent lines and concavity.
Handling of more complex scenarios where the upper bound of integration is a function of x, using the chain rule.
Dealing with variable lower bounds of integration and the impact on the derivative.
Writing the equation of a tangent line using the derivative of a function defined by an integral.
Addressing the scenario where both bounds of integration are variable with respect to x and how to find the derivative.
Integration of a function and its derivative in the context of AP Calculus exams, including multiple-choice and free-response questions.
Finding the value of a function at a specific point by plugging in the value into the integral definition.
Understanding the relationship between the derivative of a function defined by an integral and the original function.
Identifying intervals where a function is decreasing and concave up using the second derivative.
Determining points of inflection by analyzing the sign changes in the second derivative.
Finding the x-coordinates of relative maxima on the graph of a function using the first derivative test.
Calculating the absolute minimum value of a function on a closed interval by considering critical points and endpoints.
Application of L'Hôpital's Rule in calculating limits involving indeterminate forms resulting from integrals.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: