when does a particle speed up or slow down?

Nader M
7 Jan 202006:08
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the concept of a particle's acceleration by examining its position, velocity, and acceleration functions. It explains that an object speeds up when the signs of its velocity and acceleration agree. The script guides through deriving the velocity and acceleration functions, finding critical points, and creating a sign chart to determine when the particle speeds up. The analysis concludes that the object accelerates on the interval from 3 to 4 and from 5 to infinity, providing a clear understanding of the conditions for acceleration.

Takeaways
  • 📚 The problem is about determining when a particle speeds up based on its position function.
  • 🔍 An object speeds up when its velocity and acceleration have the same sign, indicating they agree in direction.
  • 📈 The velocity function is the first derivative of the position function, and the acceleration function is the second derivative.
  • 🌱 The velocity function given is \(3t^2 - 24t + 45\), and the acceleration function is the derivative of velocity, which simplifies to \(60 - 24 = 36\).
  • 🔍 To analyze the signs of velocity and acceleration, critical numbers are found by setting the velocity function equal to zero, resulting in \(t = 3\) and \(t = 5\).
  • 📊 A sign chart is used to determine the intervals where the velocity and acceleration have the same sign, indicating when the particle speeds up.
  • 📍 The critical numbers divide the number line into intervals: \(0\) to \(3\), \(3\) to \(5\), and beyond \(5\).
  • 🚀 Test values are chosen within each interval to determine the sign of the velocity and acceleration functions.
  • 🔄 The velocity function changes sign at \(t = 3\) and \(t = 5\), indicating the object's direction changes from right to left and vice versa.
  • 🔄 The acceleration function is constant and positive, except at \(t = 4\) where it is zero, indicating the object's rate of speed change.
  • 🏁 The particle speeds up during the intervals \(3 < t < 4\) and \(t > 5\), where the velocity and acceleration have the same sign.
Q & A

  • What is the main problem addressed in the script?

    -The main problem addressed is determining when a particle speeds up, based on its position function, velocity, and acceleration.

  • When does an object speed up according to the script?

    -An object speeds up when its velocity and acceleration have the same sign.

  • What functions are needed to analyze the particle's motion?

    -The velocity function and the acceleration function are needed to analyze the particle's motion.

  • How is the velocity function derived from the position function?

    -The velocity function is derived as the first derivative of the position function.

  • What are critical numbers in the context of the velocity function?

    -Critical numbers are the values of time when the velocity function is zero, indicating the particle is at rest.

  • How is the acceleration function derived?

    -The acceleration function is derived as the derivative of the velocity function, which is also the second derivative of the position function.

  • What does the script use to determine the signs of the velocity and acceleration functions?

    -The script uses a sign chart to determine the signs of the velocity and acceleration functions.

  • How are test values used in the sign chart?

    -Test values are picked within each interval on the number line to determine the sign of the velocity and acceleration functions within those intervals.

  • What intervals are found for the velocity function in the script?

    -The intervals found are between 0 and 3, 3 and 5, and beyond 5.

  • During which intervals does the particle speed up according to the script?

    -The particle speeds up in the intervals from 3 to 4 and from 5 to infinity, where the signs of velocity and acceleration agree.

Outlines
00:00
📈 Determining When a Particle Speeds Up

This paragraph explains that to determine when a particle speeds up, we need to analyze when its velocity and acceleration have the same sign. It introduces the position function and derives the velocity function using differentiation. The velocity function is then factored to find critical points where the object is at rest, which are used to create a sign chart for further analysis.

05:01
🔄 Analysis of Velocity and Acceleration Signs

This paragraph continues by analyzing the signs of the velocity function across different intervals using a sign chart. It also derives the acceleration function and uses test values to determine its sign across intervals. The paragraph concludes by combining the velocity and acceleration sign charts to identify the intervals where both have the same sign, indicating when the particle speeds up.

Mindmap
Keywords
💡Particle
In the context of this video, a 'particle' refers to an object with mass that is being studied in classical mechanics. It is a simplified representation of an object where only its mass and motion are considered, ignoring its size and shape. The script discusses the particle's position, velocity, and acceleration, which are fundamental concepts in understanding its motion.
💡Position Function
The 'position function' is a mathematical representation of an object's location over time in a given frame of reference. It is a function of time that, when evaluated, gives the position of the particle at any given moment. In the script, the position function is given as a formula, and it is the starting point for analyzing the particle's motion.
💡Velocity
Velocity is the rate of change of an object's position with respect to time. It is a vector quantity that describes both the speed and direction of the motion. The script explains that the velocity function is derived from the position function and is crucial for determining when the particle is speeding up or slowing down.
💡Acceleration
Acceleration is the rate of change of velocity with respect to time. It indicates how quickly the velocity of an object is changing and can be positive (speeding up) or negative (slowing down). The script discusses the acceleration function, which is derived from the velocity function, and its importance in determining the particle's motion dynamics.
💡Sign Chart
A 'sign chart' is a graphical tool used to determine the signs of different functions over intervals of the independent variable, in this case, time. The script uses a sign chart to analyze the signs of the velocity and acceleration functions, which helps in understanding when the particle is speeding up or slowing down.
💡Critical Numbers
Critical numbers are the values of the independent variable (time, in this case) that make the derivative of a function equal to zero or undefined. In the script, the critical numbers are found by setting the velocity function equal to zero, which gives the times when the particle is at rest.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. The script uses derivatives to find the velocity and acceleration functions from the position function, and to analyze the behavior of the particle's motion.
💡Factoring
Factoring is a mathematical process of breaking down a polynomial into a product of other polynomials. In the script, factoring is used to simplify the velocity function and find its roots, which are the critical numbers where the particle's velocity is zero.
💡Interval
In the context of this video, an 'interval' refers to a range of values for the independent variable (time) over which the behavior of the particle's motion is analyzed. The script discusses intervals between critical numbers to determine the signs of the velocity and acceleration functions.
💡Test Values
Test values are specific points within an interval chosen to evaluate the function's behavior. The script uses test values to determine the sign of the velocity and acceleration functions in different intervals, which helps in constructing the sign chart.
💡Speeding Up
The term 'speeding up' refers to the situation where an object's velocity and acceleration have the same sign, indicating that the object's speed is increasing. The script's main focus is to determine the intervals of time when the particle is speeding up by analyzing the signs of its velocity and acceleration.
Highlights

The problem focuses on determining when a particle speeds up based on its position function.

An object speeds up when its velocity and acceleration have the same sign.

The velocity function is the derivative of the position function.

The acceleration function is the second derivative of the position function.

Critical numbers are found by setting the velocity function equal to zero.

The object is at rest at times t=3 and t=5.

A sign chart is used to analyze the signs of velocity and acceleration.

The velocity function is tested for intervals between 0 and 3, 3 and 5, and beyond 5.

The acceleration function is tested for intervals between 0 and 4, and beyond 4.

The object speeds up when both velocity and acceleration are positive or both are negative.

The object is speeding up on the interval from 3 to 4 and from 5 to infinity.

The sign chart shows the intervals where the object's velocity and acceleration agree.

The object's velocity and acceleration do not agree between t=4 and t=5.

The method involves finding the roots of the velocity function and analyzing its sign intervals.

The acceleration function is simplified to 60 - 24t to find when it equals zero.

The object's speed is analyzed by considering both its direction and magnitude of velocity and acceleration.

The solution process involves a detailed examination of the particle's motion over time.

Transcripts

Browse More Related Video

Slowing Down Speeding Up Derivatives Application Calculus MCV4U

Use Position Function to Determine the Vel and Acc Funct and When Object is Speeding Up or Slowing

Particle Motion - Speeding Up and Slowing Down (Example, AP Calculus)

Particle MotionDay1

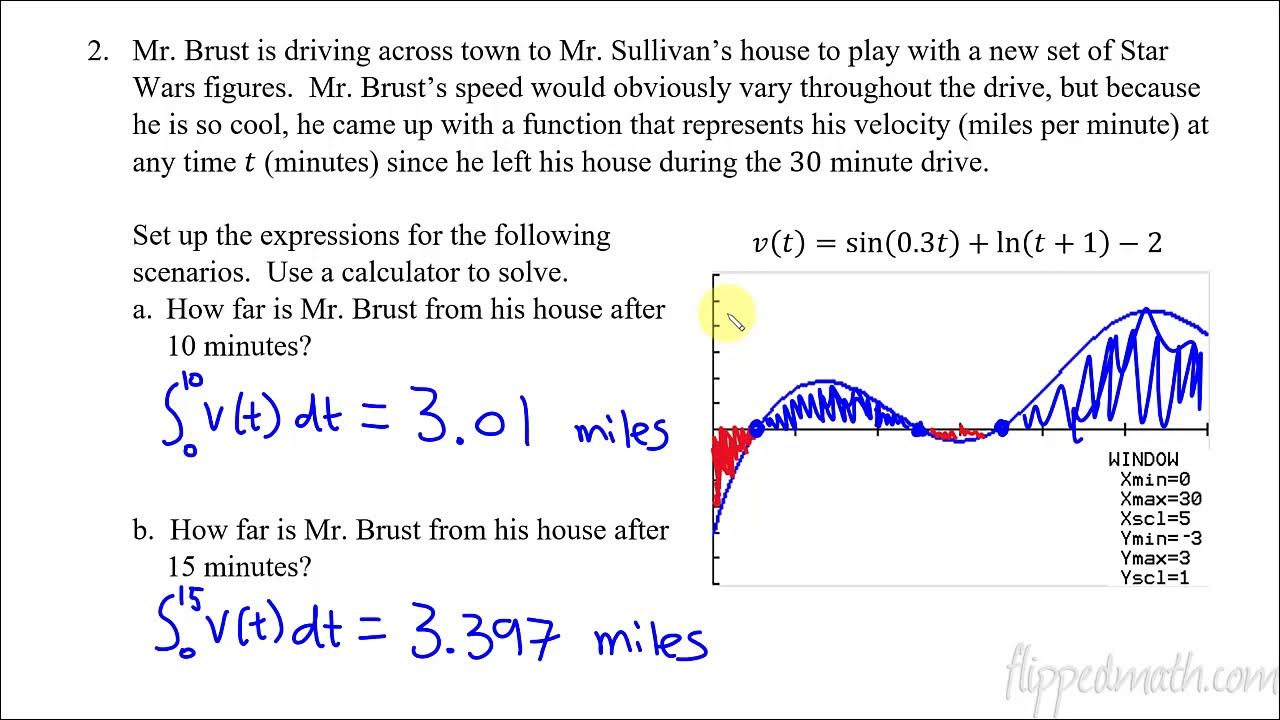
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

Position, Velocity, and Acceleration vs. Time Graphs

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsMotion AnalysisAccelerationVelocityDerivativeSign ChartCritical PointsKinematicsTime IntervalsParticle MotionSpeed Up