What is Lambda Calculus and why?

Yana the Contrarian

22 Aug 202108:51

EducationalLearning

32 Likes 10 Comments

TLDRThis script delves into the concept of lambda calculus, a foundational framework in computer science that treats functions as first-class citizens. It explores how all values are functions, and computations can be expressed through function application alone. The script provides examples of simple functions and introduces concepts like currying and boolean logic within the lambda calculus system. It also touches on the limitations, such as the absence of recursion and the necessity for syntactic sugar to make it more approachable for humans.

Takeaways

📚 Lambda calculus is a mathematical approach that focuses on functions, where all values are functions and the only operation is taking in values to apply them.
💡 In programming, functions can also be first-class citizens, meaning they can be treated like any other value, such as numbers or strings.
🔍 Lambda calculus takes the concept of functions to an extreme by asserting that everything is a function, with no other types of values or operations.
🤔 The power of lambda calculus lies in its ability to express all computations, both terminating and infinite, at a high level of abstraction.
👉 The simplest function in lambda calculus is the identity function, which takes a value and returns it unchanged.
🚫 Lambda calculus does not allow for operations like multiplication or addition; all values must be functions, and the only operation is function application.
🔄 Functions in lambda calculus can use bound variables more than once, and can also have free variables, which are not bound to any specific value.
🔑 The concept of currying is used in lambda calculus, allowing functions to bind multiple variables and return new functions that can operate on the remaining variables.
🔄 Boolean values and operations can be represented in lambda calculus using functions that take in two values and return one based on the first parameter.
🔧 Lambda calculus does not inherently support recursion, but clever techniques can be used to achieve recursive-like behavior within its constraints.
🛠 Functions in lambda calculus are often given names for human convenience, but these names are syntactic sugar and do not affect the underlying functionality.

Q & A

What is lambda calculus?
-Lambda calculus is a formal system in mathematical logic and computer science for expressing computation by way of function abstraction and application. It is based solely on function definitions and is used to describe computation processes.
How are functions represented in lambda calculus?
-In lambda calculus, functions are represented using abstraction notation, where a function is defined with a lambda symbol (λ), followed by a parameter and the expression that defines the function's behavior.
What are first-class functions in programming?
-First-class functions are a concept in programming languages where functions are treated as first-class citizens, meaning they can be passed as arguments, returned from other functions, and assigned to variables, just like any other value.
Why is lambda calculus considered to be 'all values are functions'?
-Lambda calculus is considered 'all values are functions' because it is a system where the only kind of value is a function, and all computation is expressed as the application of functions to arguments.
What is the significance of lambda calculus being 'Turing complete'?
-Lambda calculus being 'Turing complete' means that it can represent any computation that can be performed by a Turing machine, which is the theoretical basis for modern computers. This makes lambda calculus a universal model of computation.
Can you provide an example of the simplest function in lambda calculus?
-The simplest function in lambda calculus is the identity function, which can be written as 'λx.x'. It takes an input 'x' and returns the same value 'x'.
What is the concept of 'currying' in lambda calculus?
-Currying is the process of transforming a function with multiple arguments into a sequence of functions, each with a single argument. In lambda calculus, this allows a function to bind multiple variables and return another function that will perform the computation with the remaining arguments.
How can boolean values be represented in lambda calculus?
-Boolean values can be represented in lambda calculus using functions that behave like boolean operators. For example, 'true' can be a function that takes two arguments and returns the first one, and 'false' can be a function that takes two arguments and returns the second one.
What is the role of syntactic sugar in lambda calculus?
-Syntactic sugar in lambda calculus refers to names or notations that make the expressions more readable and convenient for humans but do not affect the underlying functionality of the lambda calculus. They are used to make the expressions easier to understand and work with.
How can recursion be achieved in lambda calculus?
-Recursion in lambda calculus is achieved through clever tricks and techniques since direct recursion is not allowed. It involves defining functions in such a way that they can call themselves indirectly, often by passing themselves as arguments to other functions.
What is the purpose of the 'not' function in lambda calculus as described in the script?
-The 'not' function in lambda calculus is used to invert the truth value of a boolean. It takes a boolean argument and returns its opposite. For example, if applied to 'true', it would return 'false', and vice versa.

Outlines

00:00

📚 Introduction to Lambda Calculus

This paragraph introduces the concept of lambda calculus, a theoretical framework that centers around functions. It explains how functions work in mathematics and programming, highlighting the idea of 'first-class functions' where functions can be treated as values. The speaker uses 'pencil code' as an example and mentions the concept of 'currying,' which allows for partial application of functions. The paragraph emphasizes that in lambda calculus, all values are functions, and the primary operation is the application of these functions to values, leading to a deep exploration of computation theory.

05:01

🔍 Exploring Lambda Calculus Operations and Booleans

The second paragraph delves deeper into the operations permitted within lambda calculus, focusing on the identity function and the challenges of representing arithmetic operations like multiplication due to the absence of numeric values. It then introduces the concept of boolean values in lambda calculus, demonstrating how to define and use boolean operators without traditional boolean syntax. The paragraph also touches on the limitations of lambda calculus regarding recursion and the use of function names as syntactic sugar, concluding with an invitation for the viewer to engage in a more hands-on exploration of lambda calculus expressions.

Mindmap

Keywords

💡Lambda Calculus

Lambda Calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application. It is the foundation of functional programming and plays a central role in the video as it represents the core concept being discussed. The script introduces Lambda Calculus as a way of thinking where 'all values are functions' and demonstrates how it can express any computation theoretically.

💡Functions

In the context of the video, functions are the fundamental building blocks of Lambda Calculus. They are defined as mathematical or programming constructs that take inputs, perform operations, and return outputs. The script explains how functions in Lambda Calculus are the only type of value and are used to create complex behaviors through simple function applications.

💡First-Class Functions

First-class functions are a concept in programming where functions are treated as first-class citizens, meaning they can be passed as arguments, returned from other functions, and assigned to variables. The video script uses the example of 'click' as a first-class function to illustrate how functions can be used in programming, setting the stage for the deeper dive into Lambda Calculus.

💡Identity Function

The identity function is a simple function in Lambda Calculus that takes a value and returns the same value unchanged. It serves as a basic example in the script to demonstrate the concept of function abstraction in Lambda Calculus. The identity function is used to show how functions can be represented and applied in this system.

💡Abstraction

Abstraction in Lambda Calculus refers to the process of binding a value to a variable within a function. The script explains how abstraction allows for the creation of functions that can take on different values, showcasing the flexibility and power of Lambda Calculus in expressing computations.

💡Application

Application is the process of substituting a value into a function to perform a computation. The video script describes how application is the only operation allowed in Lambda Calculus, emphasizing the importance of this concept in evaluating expressions and achieving computation.

💡Currying

Currying is a technique in Lambda Calculus where a function with multiple arguments is transformed into a sequence of functions, each accepting one argument. The script uses currying to illustrate how functions can be composed and partially applied, showing the expressive power of Lambda Calculus in handling complex operations.

💡Booleans

Booleans represent the two truth values 'true' and 'false' and are used in the video to demonstrate how Lambda Calculus can model logical operations. The script explains how boolean functions can be defined and used in Lambda Calculus to create logical expressions and operations.

💡Syntactic Sugar

Syntactic sugar refers to language features that make code easier to read or write without affecting the functionality. In the script, syntactic sugar is mentioned in relation to naming functions in Lambda Calculus, which makes the expressions more readable for humans but does not change the underlying computation.

💡Recursion

Recursion is a process where a function calls itself to solve a problem. Although not directly allowed in the basic form of Lambda Calculus as described in the script, the concept is mentioned to highlight the limitations and the need for clever techniques to achieve recursive behaviors within the system.

💡Evaluation

Evaluation in Lambda Calculus is the process of reducing expressions to their simplest form using the rules of the system. The script discusses how evaluation works, using examples of boolean functions to show how complex expressions can be simplified to a single value in Lambda Calculus.

Highlights

Lambda calculus is a way of thinking focused on functions.

Functions in programming can be used for more than just mathematical operations.

Some programming languages have first-class functions, where functions can act as values.

Lambda calculus takes the concept of functions to an extreme, with all values being functions.

In lambda calculus, functions consume values and plug them into other functions.

Lambda calculus can express both terminating and infinite computations.

All computations that can be done on a computer can theoretically be done with lambda calculus.

Lambda calculus is a powerful tool for expressing computations at a high level of abstraction.

The identity function in lambda calculus takes a value and returns the same value.

In lambda calculus, all values are functions and the only operation is taking in values to apply functions.

Lambda calculus does not allow for operations like multiplication or addition as seen in traditional mathematics.

Currying is a concept in lambda calculus where a function can bind multiple variables and return another function.

Boolean values can be represented as functions in lambda calculus.

Functions in lambda calculus can act as boolean operators, returning the appropriate value based on their inputs.

Lambda calculus does not allow for recursion in its definitions, requiring clever tricks to achieve recursion.

Syntactic sugar in programming, such as function names, does not affect the functionality of lambda calculus.

Lambda calculus expressions can be complex and may require manual manipulation for evaluation.

The speaker invites viewers to contribute to the development of an interactive lambda calculus visualizer.

Transcripts

Browse More Related Video

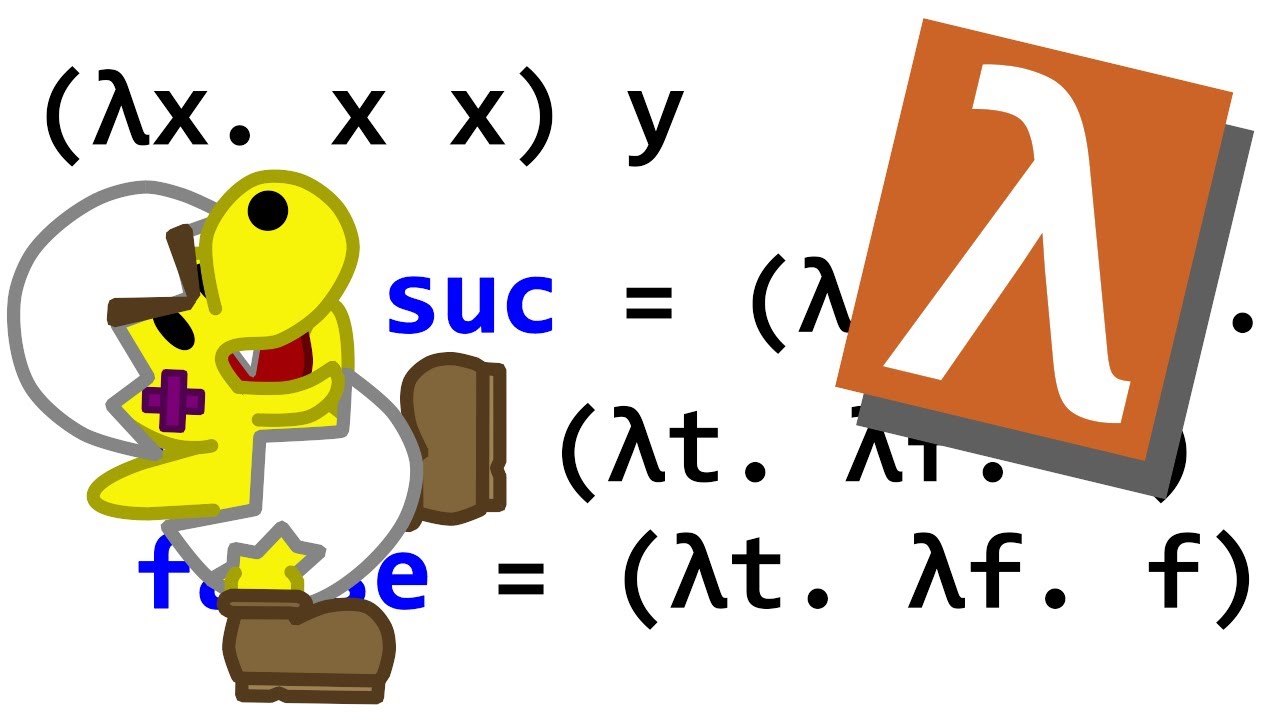
Lambda Calculus!

PLT: Lambda Calculus - Basics 1

Essentials: Functional Programming's Y Combinator - Computerphile

Lambda Calculus: The foundation of functional programming, and the simplest programming language

Lambda (λ) Calculus Primer

A Flock of Functions: Lambda Calculus and Combinatory Logic in JavaScript | Gabriel Lebec @ DevTalks

What is Lambda Calculus and why?

Takeaways

Q & A