Lambda (λ) Calculus Primer
TLDRThis video offers an insightful primer on the Lambda calculus, the foundational framework for functional programming. It begins by explaining the concept and history of Lambda calculus, then delves into defining functions through Lambda abstractions without the need for function names. The script discusses evaluation rules, including Delta rules for built-in functions, beta reduction for function application, and Alpha and ETA conversions for variable renaming and optimization. It also explores reduction orders and the implications of the Church-Rosser theorems, emphasizing the importance of understanding Lambda calculus for a solid grasp of functional programming concepts.
Takeaways
- 📚 The Lambda calculus is a formal system for expressing computation, foundational to functional programming.
- 👨🏫 Developed by Alonzo Church, the Lambda calculus uses Greek letter 'Lambda' to define expressions and terms.
- 🔍 Variants of Lambda calculus include the simple untyped, simple typed, system F, and polymorphic Lambda calculus, among others.
- 🎓 Learning Lambda calculus provides a solid theoretical base for understanding functional programming languages.
- 🤖 Lambda abstraction is the method of defining functions in Lambda calculus, using an anonymous approach without function names.
- 📝 The syntax of Lambda calculus is defined in Backus-Naur Form (BNF), which describes the language's grammar.
- 🔢 Delta rules are used for evaluating built-in functions like arithmetic operations within Lambda expressions.
- 🔄 Beta reduction is the process of applying a function to an argument by replacing the function's parameters with the argument's values.
- 🔑 Alpha conversion is necessary for renaming bound variables to avoid name capture conflicts during beta reduction.
- 🔄 ETA conversion is an optimization technique to simplify expressions by removing unnecessary Lambda abstractions.
- 🔁 The evaluation of Lambda expressions can follow different reduction orders, which may affect the outcome and efficiency of the computation.
Q & A
What is the Lambda calculus?
-The Lambda calculus is a formal system for expressing computation, developed by Alonso Church. It is used as a theoretical foundation for functional programming languages and is often considered a sort of Assembly Language for functional languages.
Why is the Lambda calculus important in functional programming?
-Understanding the Lambda calculus provides a solid base to understand the theory behind functional programming. It helps in appreciating what happens under the hood when writing code using a functional language.
What is a Lambda abstraction?
-A Lambda abstraction is a way of defining a function in the Lambda calculus. It starts with the Lambda symbol, followed by a formal parameter (e.g., 'x'), a dot, and then the function body. Lambda abstractions are anonymous functions, meaning they do not have names.
How are functions defined in the Lambda calculus?
-Functions in the Lambda calculus are defined using Lambda abstractions. The syntax involves the Lambda symbol, a formal parameter, a dot, and the function body. The function application is written in prefix form, with the function name (or Lambda abstraction) followed by its arguments.
What is the purpose of the Greek letter Lambda in the Lambda calculus?
-The Greek letter Lambda is used to denote that a Lambda abstraction is being defined. It is a key part of the syntax for defining functions within the system.
What are the evaluation rules in the Lambda calculus?
-The evaluation rules in the Lambda calculus include Delta rules for evaluating built-in functions, beta reduction for applying Lambda abstractions to their arguments, Alpha conversion for renaming variables to avoid name capture, and ETA conversion for simplifying expressions.
What is beta reduction in the Lambda calculus?
-Beta reduction is a rule used to reduce a Lambda expression to a simpler one by applying a Lambda abstraction to its argument. It involves copying the body of the Lambda abstraction and replacing all free occurrences of the formal parameter with the argument.
What is Alpha conversion and why is it necessary?
-Alpha conversion is a renaming process used in the Lambda calculus to change the name of a formal parameter and all its occurrences within a Lambda abstraction. It is necessary to prevent the name capture problem, which can occur when a variable name clashes with an inner binding.
What are the Church-Rosser theorems and what do they imply?
-The Church-Rosser theorems, also known as confluence theorems, state that if an expression can be reduced to a normal form, then there is only one such normal form. This ensures that different reduction sequences will not lead to different normal forms, provided they terminate.
What is the significance of normal form in the Lambda calculus?
-A normal form in the Lambda calculus is an expression that contains no more reducible expressions. It represents the final, simplified state of an expression after all possible reductions have been applied. The concept of normal form is important for understanding the termination and final result of Lambda calculus expressions.
What are the different reduction orders in the Lambda calculus?
-Reduction orders in the Lambda calculus determine the sequence in which reducible expressions are reduced. Two common orders are leftmost reduction (always choosing the leftmost reducible expression) and normal order reduction (reducing the leftmost outermost reducible expression until no more reducible expressions exist).
Outlines
📚 Introduction to Lambda Calculus
This paragraph introduces the Lambda calculus as a formal system for expressing computation, developed by Alonzo Church. It aims to provide a foundation for understanding functional programming. The video will cover the basics of Lambda calculus, including defining functions, the simple untyped version, evaluation rules, reduction orders, and Church-Rosser theorems. The importance of Lambda calculus in functional programming languages is emphasized, and it is likened to an Assembly Language for these languages.
🔍 Defining Functions in Lambda Calculus
The paragraph explains how to define functions in Lambda calculus using Lambda abstraction. It contrasts traditional mathematical functions with Lambda abstractions, highlighting the absence of function names and the use of prefix notation. The process of function application through juxtaposition is introduced, and an example of a simple Lambda calculus program is given to illustrate the syntax and semantics of the language.
🤔 Understanding Lambda Calculus Syntax
This section delves into the syntax of the simple untyped Lambda calculus, using Backus-Naur Form (BNF) to describe the language's grammar. It explains the recursive nature of the definition of an expression, which can include constants, variables, function applications, and Lambda abstractions. An example program calculating the multiplication of 3 and 4 is provided to demonstrate the syntax in practice.
📝 Exercises in Building Lambda Expressions
The paragraph presents an exercise for the viewer to build a sequence of Lambda expressions, starting with a given expression and applying the rules of the Lambda calculus to validate its correctness. The exercise aims to solidify the understanding of constructing and simplifying Lambda expressions, emphasizing the importance of recognizing the structure and rules of the calculus.
🔧 Evaluation Rules of Lambda Calculus
This section introduces the evaluation rules of Lambda expressions, starting with Delta rules for built-in functions and moving on to beta reduction for function application. The concept of bound and free variables is explained, which is crucial for understanding how to apply these rules correctly. Examples are provided to illustrate the process of beta reduction and the importance of identifying free variables within the function body.
🔄 Advanced Reduction Techniques
The paragraph discusses advanced reduction techniques, including Alpha conversion to address name capture problems and ETA conversion as an optimization. It provides examples to demonstrate how these techniques are applied in practice, emphasizing the importance of following the rules to avoid confusion and ensure correct reductions.
🏁 Normal Forms and Reduction Orders
This section explores the concept of normal forms in Lambda calculus, which represent the final state of an expression with no more reducible parts. It explains the difference between reduction orders and how they can affect the outcome of an expression. The Church-Rosser theorems are introduced, ensuring that all terminating reduction sequences lead to the same normal form, and that there exists a normal order reduction sequence for any terminating expression.
📘 Conclusion and Practical Implications
The final paragraph wraps up the video by summarizing the key points covered on Lambda calculus, its theoretical foundations, and its practical implications for functional programming. It highlights the importance of understanding Lambda calculus for anyone looking to work with functional programming languages and encourages viewers to apply this knowledge in their coding endeavors.
Mindmap
Keywords
💡Lambda calculus
💡Functional programming
💡Lambda abstraction
💡Untyped Lambda calculus
💡Evaluation rules
💡Beta reduction
💡Alpha conversion
💡Church-Rosser theorems
💡Normal form
💡Reduction order
💡Type systems
Highlights
The Lambda calculus is a formal system for expressing computation, developed by Alonso Church.
The Greek letter Lambda is used to define expressions and terms within the Lambda calculus system.
The Lambda calculus serves as a foundational theory for functional programming languages.
Higher-level functional programming languages often translate their source code into a form of Lambda calculus.
Functions in the Lambda calculus are defined using Lambda abstraction, which is an anonymous function.
Lambda abstraction uses prefix notation, where the function is written before its arguments.
The simple untyped Lambda calculus is the focus of the course, with other variants like typed Lambda calculus and system F mentioned for further study.
Lambda calculus can be thought of as an Assembly Language for functional languages.
The syntax of the Lambda calculus is defined using Backus-Naur Form (BNF), which describes the language's grammar.
A Lambda calculus program is a single expression that is executed by evaluating this expression.
Delta rules are used to evaluate built-in functions within the Lambda calculus.
Beta reduction is a key rule for reducing Lambda expressions, involving the application of a Lambda abstraction to its argument.
Alpha conversion is necessary to rename variables within a Lambda expression to avoid name capture problems.
ETA conversion is an optimization that allows the simplification of Lambda expressions by eliminating unnecessary abstractions.
Reduction orders determine the sequence in which expressions are reduced, impacting the outcome and efficiency of evaluation.
The Church-Rosser theorems ensure that if an expression has a normal form, all reduction sequences that terminate will reach the same result.
Understanding the Lambda calculus provides a solid base for grasping the theory behind functional programming.
The video concludes by emphasizing the importance of the Lambda calculus in the practical application of functional programming languages.
Transcripts
Browse More Related Video

lambda calculus review

Lambda Calculus: The foundation of functional programming, and the simplest programming language

What is Lambda Calculus? (ft. Church Encodings)
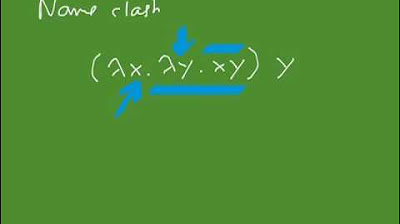
The Lambda Calculus, part 1 1 Syntax and semantics

L16: Lambda Calculus Introduction

A Flock of Functions: Lambda Calculus and Combinatory Logic in JavaScript | Gabriel Lebec @ DevTalks
5.0 / 5 (0 votes)
Thanks for rating: