Measures of Variability (Variance, Standard Deviation, Range, Mean Absolute Deviation)
TLDRThis script explores various measures of variability, such as range, mean absolute deviation, variance, and standard deviation, highlighting their importance in practical applications like packaging consistency and stock options. It emphasizes the use of squared deviations to better estimate population variance and introduces the empirical rule for interpreting standard deviation in mound-shaped distributions.
Takeaways
- 📦 Variability in a variable, such as the weight of packaged food or a stock's price, is crucial in practical situations.
- 🔢 The range, calculated as the difference between the maximum and minimum values, is a simple measure of variability but lacks detail about the spread of values.
- 📊 Deviations from the mean are the basis for better measures of variability. Each observation's deviation is its value minus the mean.
- 📈 The mean absolute deviation (MAD) is the average distance from the mean, calculated by taking the mean of the absolute values of the deviations.
- ❌ The sum of deviations from the mean always equals zero, making it less useful for measuring variability.
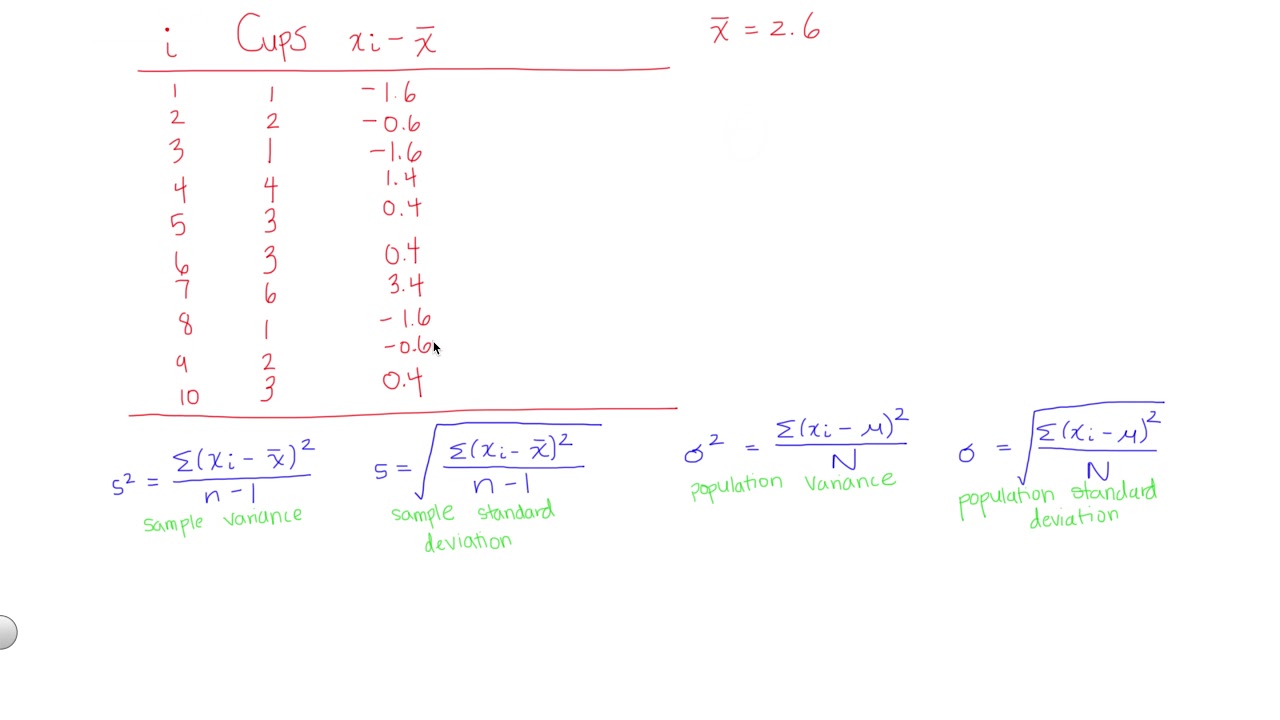
- 📉 The sample variance (s²) is calculated by summing the squared deviations and dividing by n-1, providing a better estimate of the population variance than dividing by n.
- 📚 The standard deviation is the square root of the variance, and it shares the same units as the variable, making it a more intuitive measure of variability.
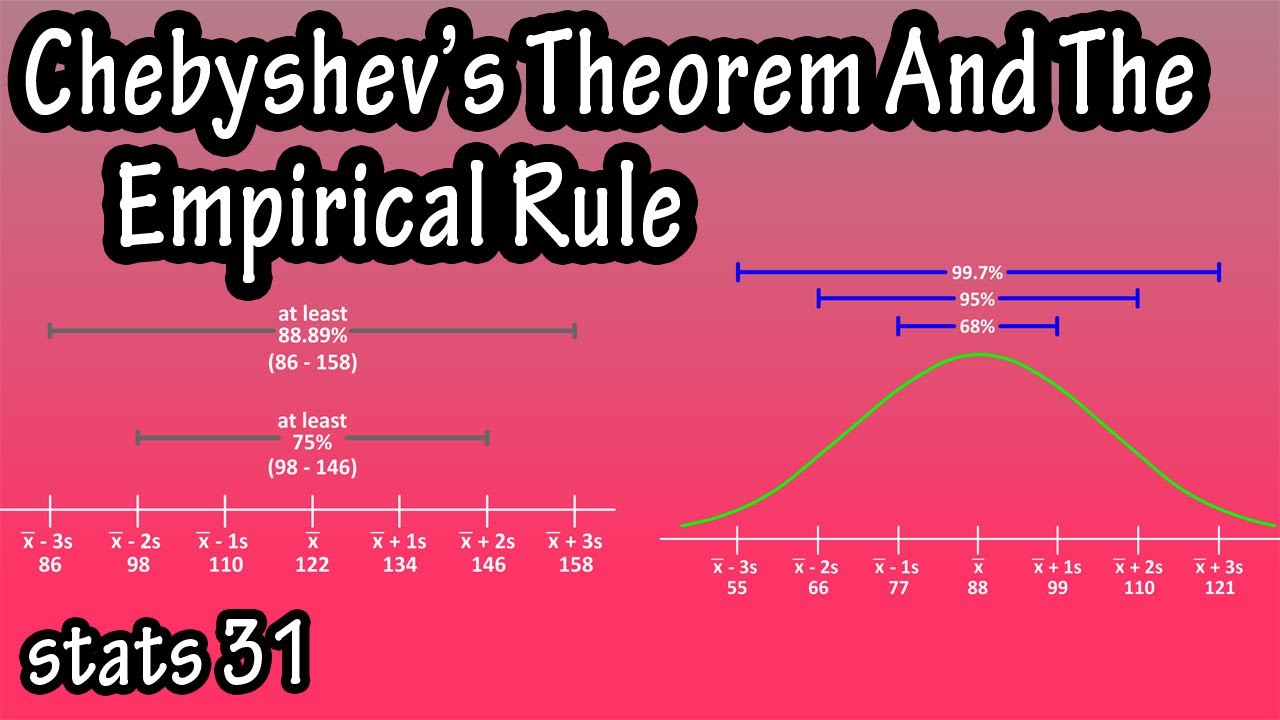
- 🔍 The empirical rule states that for mound-shaped distributions, approximately 68% of observations lie within one standard deviation of the mean, 95% within two, and almost all within three.
- 📊 The variance and standard deviation can be sensitive to extreme values, which can inflate these measures and affect their interpretation.
- 💻 It's recommended to use software or calculators to calculate variance and standard deviation, as manual calculations can be prone to errors and are less efficient.
Q & A
What is variability, and why is it important?
-Variability, or dispersion, measures how much the values of a variable differ from each other. It's important in practical situations, such as ensuring consistent product weight in packaged foods or determining stock price fluctuations for pricing options.
How is the range of a data set calculated?
-The range is calculated by subtracting the smallest observation from the largest observation in the data set. For example, with observations 45, 51, 64, and 68, the range is 68 - 45 = 23.
What are deviations, and why are they important in measuring variability?
-Deviations are the differences between each observation and the mean of the data set. They are important because they help measure the spread of the data around the mean.
Why is the mean absolute deviation not often used in statistical inference methods?
-While the mean absolute deviation is a useful descriptive measure, it is not often used in statistical inference methods because working with squared deviations provides better results.
What is the formula for sample variance, and why do we divide by n-1 instead of n?
-The sample variance (s^2) is calculated as the sum of squared deviations divided by (n-1). Dividing by (n-1) instead of n results in a better estimator of the population variance, known as an unbiased estimator.
How do you interpret the variance and standard deviation?
-The variance is the average squared distance from the mean, and the standard deviation is the square root of the variance, providing a measure of spread in the same units as the data. Larger values indicate greater variability.
What is the empirical rule, and how does it help interpret the standard deviation?
-The empirical rule states that for mound-shaped (approximately normal) distributions, about 68% of observations lie within one standard deviation of the mean, 95% within two, and almost all within three. It helps to understand the dispersion of data around the mean.
Why are variance and standard deviation sensitive to extreme values?
-Because both involve squared deviations, extreme values (very large or small) can disproportionately increase the variance and standard deviation, inflating these measures.
What alternative formula can be used to calculate the variance, and why might it be used?
-An alternative calculation formula for variance can help reduce roundoff error in hand calculations. However, it's less common today due to reliance on software or calculators.
Why is it recommended to use software or calculators for calculating variance and standard deviation?
-Using software or calculators is recommended because it reduces the calculation burden, minimizes errors, and is more efficient, especially with large data sets.
Outlines
📏 Understanding Variability Measures
This paragraph introduces the concept of variability in data and its importance in practical situations, such as in packaging food or pricing stock options. It starts by explaining the range as a simple measure of variability, which is the difference between the maximum and minimum values in a dataset. However, the range is limited in its usefulness as it does not account for the spread of values within these extremes. The paragraph then delves into more sophisticated measures based on deviations from the mean. Deviations are the differences between each observation and the mean, and the mean absolute deviation (MAD) is introduced as the average of these absolute deviations. While MAD provides a simple interpretation of the average distance from the mean, it is not commonly used in statistical inference. The focus then shifts to squared deviations, which form the basis for calculating the sample variance (s^2). The variance is the sum of squared deviations divided by (n-1), and it is used to estimate the population variance. The paragraph concludes by discussing the limitations of using the sum of deviations and the advantages of using squared deviations in statistical analysis.
📉 Exploring Variance and Standard Deviation
This paragraph further explores the concepts of variance and standard deviation. It begins by discussing the variance as the average squared distance from the mean, emphasizing that the units of variance are squared units of the variable. To revert to the original units, the square root of the variance, known as the standard deviation, is often used. The standard deviation is shown to be always greater than or equal to zero, and it is zero only when all observations in the dataset are equal. The paragraph illustrates how the standard deviation is calculated from the squared deviations, using the formula for the sample variance and then taking its square root. An example is provided using birth weights of Canadian boys, showing how the mean absolute deviation, variance, and standard deviation are calculated from the data. The paragraph also highlights the sensitivity of variance and standard deviation to extreme values, which can inflate these measures. Finally, the empirical rule is introduced as a guideline for interpreting standard deviation in mound-shaped distributions, stating that approximately 68% of observations lie within one standard deviation of the mean, 95% within two standard deviations, and almost all within three standard deviations.
🔍 Empirical Rule and Calculation Tips
The final paragraph of the script discusses the empirical rule in more detail, providing a visual representation of how data is distributed around the mean in a mound-shaped distribution. It explains that the empirical rule helps interpret the standard deviation by indicating the percentage of observations that fall within one, two, or three standard deviations of the mean. The paragraph also mentions an alternative formula for calculating the sample variance, which can help reduce roundoff error in manual calculations. However, it emphasizes the importance of using software or calculators for these calculations, as they are more efficient and accurate. The speaker recommends learning to use these tools to calculate variance and standard deviation, suggesting that manual calculations are useful for understanding the concepts but not practical for routine analysis.
Mindmap
Keywords
💡Variability
💡Range
💡Deviation
💡Mean Absolute Deviation (MAD)
💡Variance
💡Standard Deviation
💡Sample Variance
💡Empirical Rule
💡Squared Deviations
💡Statistical Inference
💡Histogram
Highlights
The variability or dispersion of a variable is crucial in practical situations such as packaged food producers wanting consistent product weight and the importance of stock price variability in pricing stock options.
The range is a simple measure of variability, calculated as the difference between the largest and smallest observations.
The range is not a great measure of variability as it doesn't reflect the spread of values between the maximum and minimum.
Better measures of variability are based on deviations from the mean, where each observation has a deviation calculated as the value minus the mean.
The sum of deviations for any data set is always zero, making it not useful for measuring variability.
Mean absolute deviation is the mean of the absolute value of deviations, representing the average distance from the mean.
Mean absolute deviation is a simple interpretation of variability but is not commonly used in statistical inference methods.
The sample variance is calculated by summing squared deviations and dividing by n-1, providing a better estimator of the population variance.
The standard deviation is the square root of the variance, having the same units as the variable and reflecting the average squared distance from the mean.
Both variance and standard deviation are non-negative, with zero values indicating no variability in the dataset.
The empirical rule provides a guideline for interpreting standard deviation in mound-shaped distributions, stating that approximately 68% of observations lie within one standard deviation of the mean.
The empirical rule also states that approximately 95% of observations lie within two standard deviations of the mean.
The empirical rule suggests that all or almost all observations lie within three standard deviations of the mean in mound-shaped distributions.
The standard deviation is always slightly larger than the mean absolute deviation, influenced by the shape of the distribution.
Variance and standard deviation can be sensitive to extreme values, which can inflate these measures.
An alternative formula for sample variance can help reduce roundoff error in hand calculations, though it's less commonly used with modern software and calculators.
It is recommended to use software or calculators for calculating variance and standard deviation to offload the calculation burden.
Transcripts
Browse More Related Video
How to Calculate Standard Deviation and Variance by Hand

Statistics: Standard deviation | Descriptive statistics | Probability and Statistics | Khan Academy

Measures of Variability (Range, Standard Deviation, Variance)

Statistics Lecture 3.3: Finding the Standard Deviation of a Data Set
What Is And How To Use Chebyshev's Theorem And The Empirical Rule Formula In Statistics Explained

Variance and Standard Deviation: Why divide by n-1?
5.0 / 5 (0 votes)
Thanks for rating: