Lecture 5: Conditioning Continued, Law of Total Probability | Statistics 110
TLDRIn this lecture, the professor delves into the intricacies of conditional probability, emphasizing its significance not only in statistics but as a fundamental tool for reasoning under uncertainty. He revisits Bayes' Rule and introduces the law of total probability, illustrating these concepts with practical examples, including problem-solving strategies like partitioning complex problems into simpler components. The lecture also explores real-world applications, such as medical testing, highlighting common misconceptions in interpreting statistical data. Through examples like the Sally Clark legal case, the lecture underscores the critical role of accurate statistical understanding in various fields.
Takeaways
- 💭 Conditional probability is crucial for understanding how to update our beliefs in the presence of new evidence, underpinning much of statistical reasoning.
- 🔥 The law of total probability helps break down complex probability problems into simpler, more manageable parts by utilizing a partition of the sample space.
- 🎲 Strategies such as trying simple cases, using extreme examples, and decomposing problems into smaller pieces are emphasized as effective problem-solving techniques.
- 📊 The Bayes' rule is essential for converting the probability of observing evidence given an event (like a disease) into the probability of an event given observed evidence, crucial for medical testing interpretations.
- 🧪 Misinterpretations common in probability, such as confusing P(A|B) with P(B|A) or ignoring the prior probability of an event, can lead to significant consequences, as illustrated by legal examples.
- 🚩 The importance of conditional independence versus unconditional independence is highlighted, explaining that dependencies can alter under different conditions.
- 📝 Real-life applications of statistical methods in law, medicine, and daily problem-solving show the practical relevance and necessity of a deep understanding of these concepts.
- 🚀 Feynman's problem-solving algorithm humorously illustrates the need for developing robust problem-solving strategies beyond simplistic approaches.
- 🏆 Frequent misconceptions about test accuracy and the impact of rare diseases are illustrated through medical testing scenarios, demonstrating the importance of a thorough understanding of statistical reasoning.
- 🖥 The class discourse integrates frequent examples and problem-solving strategies, fostering a deep understanding of how to apply statistical concepts practically.
Q & A
What is the main theme of the course described in the transcript?
-The main theme of the course is the application of probability theory to understand uncertainty and randomness, emphasizing conditional probability and thinking conditionally as core concepts for problem solving and decision making.
What is Bayes' Rule and why is it important in the context of this course?
-Bayes' Rule is a fundamental theorem in probability that describes how to update the probability of a hypothesis based on new evidence. It is crucial in the course for teaching students how to update their beliefs in the presence of new data, particularly in scenarios involving uncertainty.
How does the instructor suggest solving problems using simple and extreme cases?
-The instructor recommends solving problems by trying simple and extreme cases as a strategy to understand the broader implications and potential edge cases of the problem. This method helps in grasping the essential elements and possible outcomes in various scenarios.
What does the instructor mean by 'thinking conditionally'?
-Thinking conditionally refers to the ability to consider variables and outcomes in the context of specific conditions or assumptions. It involves understanding how the likelihood of events changes when other relevant information is taken into account.
What is the Law of Total Probability, and how is it applied in the script?
-The Law of Total Probability is used to compute the probability of an event by breaking it down into simpler, mutually exclusive components that cover all possibilities. In the script, the instructor uses it to break down the probability of a complex event, B, into smaller probabilities that sum up to the total probability of B.
What did the instructor illustrate using the disease testing scenario?
-The instructor used the disease testing scenario to illustrate the common confusion between the probability of testing positive given the disease (P(T|D)) and the probability of having the disease given a positive test result (P(D|T)). He emphasized the importance of correctly interpreting test results and probabilities to avoid misconceptions.
Can you explain the Sally Clark case mentioned in the script and its relevance to statistical errors?
-The Sally Clark case involved a British woman wrongly convicted of murdering her children based on flawed statistical reasoning. The prosecution used extremely low probabilities of two children dying of natural causes independently to argue her guilt. This case exemplifies the 'prosecutor's fallacy', highlighting the dangers of misinterpreting conditional probabilities and ignoring context like dependency between events.
What is the significance of conditional independence in statistics?
-Conditional independence refers to the scenario where two events are independent under certain conditions or given another event. It is significant in statistics as it allows simplification of complex probability calculations by assuming independence under specific conditions.
How does the instructor use the concept of partitioning in probability?
-The instructor explains partitioning as a method to solve complex problems by dividing them into simpler, non-overlapping parts. By finding the probabilities of these simpler parts and summing them, one can determine the total probability of the original problem, simplifying analysis and computation.
What advice does the instructor give about the use of Bayes' Rule in real-life applications?
-The instructor advises that Bayes' Rule should be used with understanding of its conditions and implications, particularly in distinguishing between P(T|D) and P(D|T). This is crucial for correct decision-making in real-world scenarios, like medical testing, where the consequences of misinterpretation can be significant.
Outlines
📘 Conditional Probability and Problem Solving Techniques
The lecture starts with a recap of previous lessons, emphasizing the simplicity yet subtlety required in applying mathematical theorems to real-world problems, particularly in conditional probability. The focus shifts to problem-solving strategies, using examples from physics, and introduces Richard Feynman's straightforward problem-solving algorithm. The professor emphasizes breaking down complex problems into simpler components using conditional probability, illustrated with a Venn diagram exercise to determine probabilities in a partitioned set, reinforcing the law of total probability.
🃏 Examples of Conditional Probability with Card Games
This segment dives into practical applications of conditional probability through card games. Starting with a scenario involving aces from a standard deck, the professor calculates the probability of both cards being aces given that one ace is already in hand, and further refines the problem by specifying one card as the ace of spades. This detailed walkthrough not only demonstrates calculating conditional probabilities but also highlights the complexities and subtleties involved, especially when initial conditions or 'givens' change the dynamics of probability.
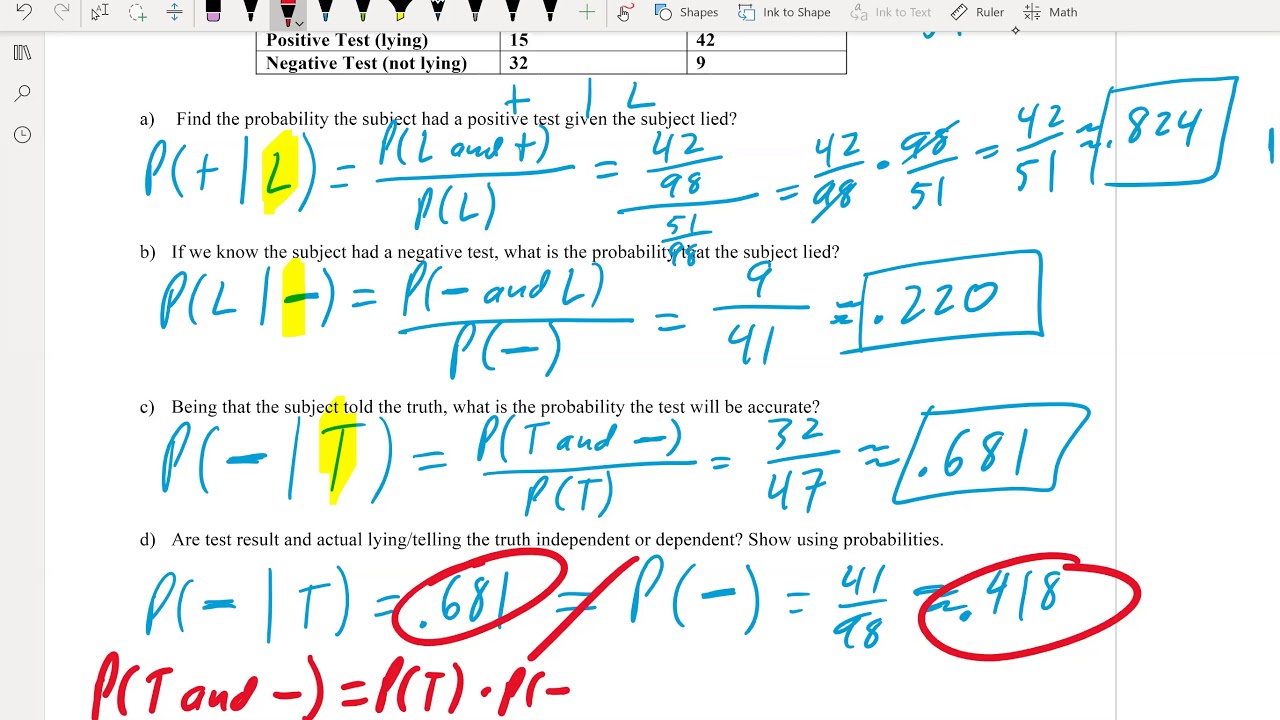
🏥 Medical Testing and Bayes' Rule
In a shift towards everyday relevance, the lecture discusses the application of conditional probability in medical testing. The professor describes a scenario where a disease affects 1% of a population and a test that is 95% accurate. Using Bayes' Rule, the professor corrects common misconceptions between P(D|T) (probability of disease given a positive test) and P(T|D) (probability of a test being positive given the disease), elucidating why the patient’s actual risk of having the disease is much lower than perceived. The segment ends by stressing the importance of understanding the base rate fallacy and the distinction between test accuracy and the likelihood of disease.
⚖️ Conditional Probability in Legal Contexts
The final segment discusses the critical application of conditional probability in legal settings, focusing on the prosecutor's fallacy and its impact on wrongful convictions. The professor references the Sally Clark case to illustrate how statistical misunderstandings can lead to tragic outcomes. Emphasizing the difference between the probability of evidence given innocence versus the probability of innocence given evidence, this part highlights how Bayesian thinking must be applied carefully to avoid grave errors in reasoning.
Mindmap
Keywords
💡Conditional Probability
💡Bayes' Rule
💡Partition
💡Law of Total Probability
💡Venn Diagram
💡Theorems
💡Factorial
💡Randomness
💡Algorithm
💡Evidence
Highlights
Proved multiple theorems on conditional probability, emphasizing Bayes Rule and its applications.
Introduced the course as not only a statistics course but also a critical thinking and problem-solving course.
Discussed the importance of thinking conditionally and applying this thinking to solve problems effectively.
Explained the use of simple and extreme cases as a problem-solving strategy in statistics and beyond.
Highlighted the general problem-solving algorithm attributed to Richard Feynman: Write down the problem, think hard, write down the solution.
Emphasized breaking problems into simpler, manageable parts as a fundamental strategy in problem-solving.
Used Venn diagrams to demonstrate how to break down a complex problem (finding the probability of event B) into simpler parts.
Introduced the Law of Total Probability as a method to handle complex probability problems by decomposing them into simpler pieces.
Explored real-world applications of conditional probability with practical examples such as card games.
Analyzed a medical testing scenario to illustrate how conditional probability is crucial in determining the likelihood of a disease given a positive test result.
Distinguished between P(T given D) and P(D given T) using Bayes' rule, clarifying common misconceptions in medical testing accuracy.
Provided a clear example of how the Law of Total Probability can be applied to calculate the probability of a patient having a disease based on test results and disease prevalence.
Emphasized the importance of understanding the impact of rare events in probability calculations, particularly in medical contexts.
Highlighted the misinterpretation risks in statistics, referencing a real-world case where misunderstanding statistical principles led to wrongful conviction.
Discussed the crucial distinction between independence and conditional independence in probability, with practical examples to illustrate the concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: