Ch. 11.3 Hyperbolas

Prof. Williams

28 Apr 202222:52

EducationalLearning

32 Likes 10 Comments

TLDRThis video script delves into the mathematical concept of hyperbolas, a type of conic section formed by the intersection of a plane with a double-napped cone. It explains the constant difference property of distances from any point on the hyperbola to its two foci, termed 2a. The script also covers the orientation, vertices, foci, and asymptotes of hyperbolas, and their representation in equations. Notably, it discusses the Hubble Space Telescope's unique use of hyperbolic mirrors in its mirror system, contrasting it with the more common parabolic mirrors in telescopes, and provides a detailed mathematical modeling of the Hubble's mirror configuration.

Takeaways

📚 The class is discussing Chapter 11.3 on hyperbolas, which are part of the conic sections and have unique properties compared to other conic sections like ellipses and parabolas.
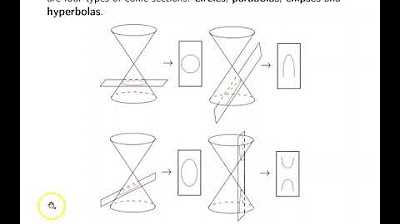
🔍 Hyperbolas are formed by the intersection of a conic with an orthogonal plane and have two distinct branches, unlike the single continuous curve of an ellipse or a parabola.
🔗 Hyperbolas have two foci, similar to ellipses, but the foci are located within the direction of concavity, and the hyperbola's branches extend infinitely in opposite directions.
⚖️ The defining characteristic of a hyperbola is that the difference between the distances from any point on the hyperbola to the two foci is a constant value, 2a.
📏 The transverse axis of a hyperbola is the line segment between the two vertices and has a length of 2a, which is crucial for understanding the hyperbola's shape and orientation.
📐 The equation of a hyperbola involves the relationship between a, b, and c, where c squared equals a squared plus b squared, reflecting the geometric properties of the hyperbola.
📈 Hyperbolas have slant asymptotes, which are lines that the hyperbola approaches but never intersects, and their equations depend on the hyperbola's orientation.
📉 The orientation of the hyperbola is determined by the sign of the variable in the squared term of its equation, with the transverse axis lying along the axis with the positive squared term.
🌌 The Hubble Space Telescope uses a unique mirror system with two hyperbolic mirrors instead of the traditional parabolic and hyperbolic combination found in other telescopes.
🔭 The Hubble's hyperbolic mirrors are designed to focus incoming light to a common focal point, extending the focal length and enhancing the telescope's imaging capabilities.
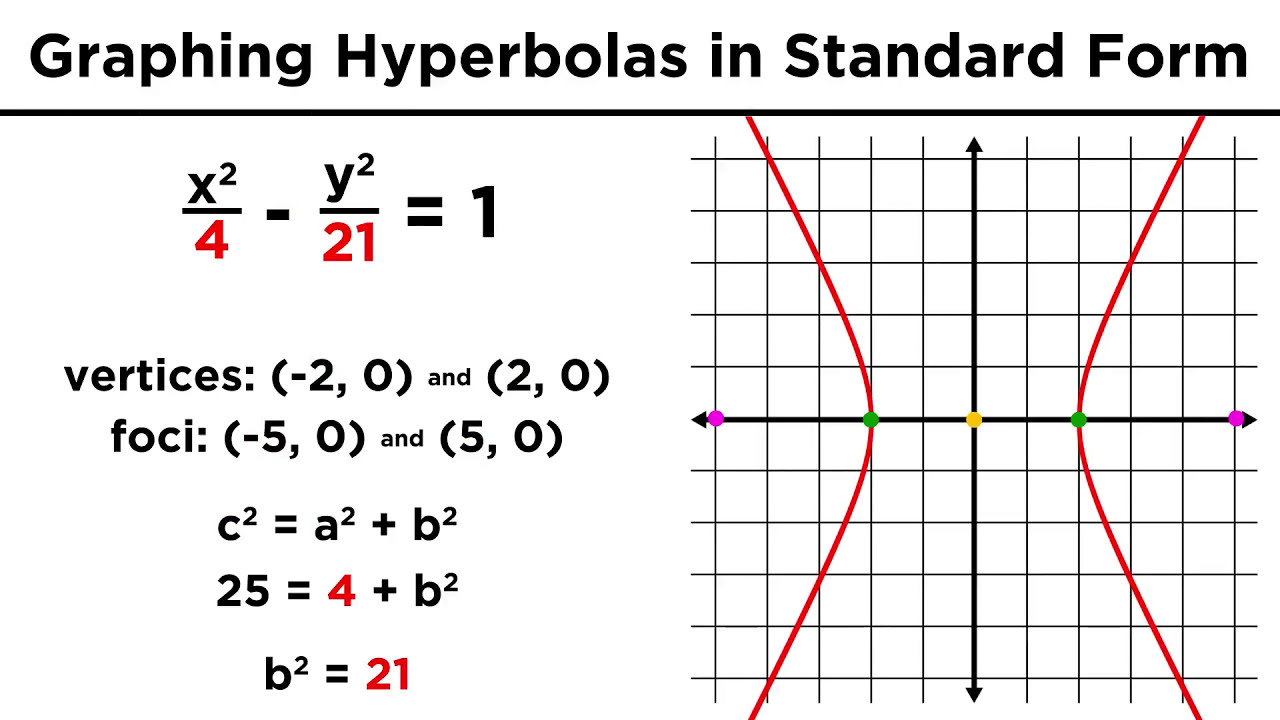
📝 The script provides a detailed explanation of how to derive the equation of a hyperbola from its graph, including determining the values of a, b, and c, and understanding the significance of the central box and slant asymptotes.

Q & A

What is the main topic of Chapter 11.3 in the script?
-The main topic of Chapter 11.3 is hyperbolas, discussing their definition, properties, and how they differ from other conic sections like parabolas and ellipses.
What is the definition of a hyperbola in terms of its intersection with a plane?
-A hyperbola is the intersection of a conic section with an orthogonal plane, which is perpendicular to the base of the conic.
How does the distance between a point on a hyperbola and its foci differ from that in an ellipse?
-In an ellipse, the sum of the distances from a point to the two foci is constant. In contrast, for a hyperbola, the difference between the distances from a point to the two foci is constant.
What are the two parts of a hyperbola called?
-The two parts of a hyperbola are called branches, each resembling a hyperbolic arc.
What is the transverse axis in the context of a hyperbola?
-The transverse axis of a hyperbola is the distance between one vertex to the other, and it is also the length of the segment connecting the two vertices.
What is the relationship between the distances from the center to the vertices and the length of the transverse axis?
-The distance from the center to a vertex (denoted as 'a') determines the length of the transverse axis, which is 2a, because the difference in distances from any point on the hyperbola to the foci is always 2a.
How is the distance from the center to the foci (denoted as 'c') related to 'a' and 'b' in a hyperbola?
-In a hyperbola, the distance from the center to the foci (c) is related to 'a' and 'b' by the equation c^2 = a^2 + b^2, which is a form of the Pythagorean theorem where 'c' is considered the hypotenuse.
What are the equations of the slant asymptotes of a hyperbola?
-The equations of the slant asymptotes of a hyperbola are given by y = (b/a)x ± b or y = (a/b)x ± a, depending on the orientation of the hyperbola.
What is the standard form of the equation of a hyperbola when its transverse axis lies on the x-axis?
-When the transverse axis of a hyperbola lies on the x-axis, the standard form of its equation is x^2/a^2 - y^2/b^2 = 1.
How does the orientation of the hyperbola affect the equation of its slant asymptotes?
-The orientation of the hyperbola affects the sign and the variables in the equation of its slant asymptotes. If the transverse axis is vertical, the asymptotes are y = (a/b)x ± a, and if it's horizontal, they are y = (b/a)x ± b.
What is the significance of the Hubble Space Telescope's mirror system in the context of hyperbolas?
-The Hubble Space Telescope uses a mirror system that involves two hyperbolic mirrors instead of the traditional parabolic and hyperbolic combination found in other telescopes. This system allows for the elimination of spherical aberration and provides a longer focal length.
How does the Hubble Space Telescope's mirror system model the properties of hyperbolas?
-The Hubble Space Telescope's mirror system models the properties of hyperbolas by using two hyperbolic mirrors that focus light towards a common focal point, demonstrating the principles of hyperbolic geometry and optics.

Outlines

00:00

📚 Introduction to Hyperbolas and Conic Sections

This paragraph introduces Chapter 11.3, which focuses on hyperbolas as the final conic section to be discussed. It explains that hyperbolas are the intersection of a conic with an orthogonal plane, resulting in two 'branches' that resemble parabolas but are distinct. The paragraph details the properties of hyperbolas, including foci, vertices, the transverse axis, and the constant difference of 2a between the distances from any point on the hyperbola to the two foci. It also introduces the concept of the central rectangle and the hyperbola's asymptotes, emphasizing the mathematical relationships between these elements.

05:04

📐 Hyperbola Characteristics and Equation Derivation

The second paragraph delves deeper into the characteristics of hyperbolas, discussing vertices, foci, and the central rectangle. It explains how the orientation of the hyperbola's transverse axis affects the equation form, with x² or y² being positive depending on the axis' alignment with the coordinate axes. The paragraph also illustrates how to derive the equation of a hyperbola from its graph, using the given values for 'a' and the slope of the asymptotes to find 'b', and subsequently 'c', using the relationship c² = a² + b².

10:06

🔭 The Hubble Space Telescope and Hyperbolic Mirrors

This paragraph introduces the Hubble Space Telescope's unique use of hyperbolic mirror systems, contrasting them with the more common parabolic mirrors found in standard telescopes. It explains that the Hubble uses a Ritchey-Chretien system, which employs two hyperbolic mirrors instead of a parabolic and hyperbolic combination. The paragraph discusses how light reflects off the convex side of a hyperbolic mirror towards the concave side of a secondary mirror, detailing the focal lengths and distances involved in the Hubble's mirror system.

15:07

🛰️ Modeling the Hubble Space Telescope's Mirror System

The fourth paragraph provides a step-by-step explanation of how to model the Hubble Space Telescope's mirror system using mathematical equations. It assigns labels to the primary and secondary mirrors (M1 and M2), identifies the vertices, and calculates the focal lengths and distances between the mirrors. The paragraph demonstrates how to derive the equations for both mirrors, considering their respective focal points and the distance between them, ultimately providing the equations for the hyperbolic mirrors that form the basis of the Hubble's optical system.

20:07

🔍 Calculating the Secondary Mirror's Equation

The final paragraph concludes the discussion on the Hubble Space Telescope's mirror system by focusing on the secondary mirror (M2). It explains the necessity for the interior focal points of both mirrors to align and calculates the distances involved to determine the values for 'a', 'b', and 'c'. The paragraph then derives the equation for the secondary mirror, considering its transverse axis length, the distance to the focus, and the relationship between these values to find 'b' squared, ultimately providing the complete equation for M2.

Mindmap

Keywords

💡Hyperbola

A hyperbola is a type of conic section formed by the intersection of a plane and a double cone, resulting in two separate curves that resemble mirror-image parabolas. In the video, the hyperbola is described as having two foci and two branches, with the defining property that the difference in distances from any point on the hyperbola to the two foci is constant (2a). The script discusses the orientation of the hyperbola and its mathematical representation, including its vertices, foci, and asymptotes.

💡Conic Sections

Conic sections are curves obtained as the intersection of a plane and a double cone. They include circles, ellipses, parabolas, and hyperbolas. The video script focuses on the hyperbola as the last conic section to be discussed, indicating that previous sections have covered the other types, and the remainder of the chapter will explore their applications.

💡Vertices

In the context of a hyperbola, vertices are the points where the curve changes direction. The script specifies that for a hyperbola, the vertices are located at a distance 'a' from the center along the transverse axis. They are crucial for defining the shape and orientation of the hyperbola.

💡Foci

Foci are two points inside the concavity of a hyperbola, equidistant from the center along the transverse axis. The script explains that the hyperbola's defining constant involves the difference in distances from any point on the hyperbola to these two foci. The foci are essential in determining the hyperbola's orientation and shape.

💡Transverse Axis

The transverse axis is the line segment that passes through the vertices of a hyperbola and is perpendicular to the conic's base. The script mentions that the length of the transverse axis is 2a, which is a key parameter in the hyperbola's geometry and is used to find the equation of the hyperbola.

💡Asymptotes

Asymptotes are lines that a hyperbola approaches but never intersects. The script describes two slant asymptotes for a hyperbola, which are related to the 'a' and 'b' parameters of the hyperbola's equation. They are crucial for sketching the hyperbola and understanding its behavior at infinity.

💡Constant Difference (2a)

The constant difference (2a) is a defining characteristic of a hyperbola, representing the fixed difference in distances from any point on the hyperbola to its two foci. The script uses this concept to explain the hyperbola's unique property and to derive its standard equation.

💡Cassegrain System

The Cassegrain system is a type of optical system used in telescopes, which traditionally uses a parabolic primary mirror and a hyperbolic secondary mirror. The script mentions the Hubble Space Telescope, which deviates from the standard by using two hyperbolic mirrors instead, a configuration known as the Ritchey-Chretien system.

💡Ritchey-Chretien System

The Ritchey-Chretien system is a variation of the Cassegrain system where both the primary and secondary mirrors are hyperbolic. The script explains that this system is used in the Hubble Space Telescope to avoid spherical aberrations and to achieve a longer focal length.

💡Focal Length

Focal length is the distance from the center of a lens or mirror to the point where parallel light rays converge or from which they appear to diverge. In the context of the script, the focal lengths of the Hubble Space Telescope's primary and secondary mirrors are discussed, which are crucial for understanding the telescope's optical properties and capabilities.

💡Equation of a Hyperbola

The equation of a hyperbola is a mathematical representation that describes its shape and position in a coordinate system. The script provides the standard form of the hyperbola's equation, which depends on the parameters 'a' and 'b', and illustrates how to derive it from the graph of a hyperbola.

Highlights

Introduction to hyperbolas as the intersection of a conic section with an orthogonal plane.

Hyperbolas have two foci located within the direction of concavity, centered along the transverse axis.

The defining property of a hyperbola where the difference between distances from any point to the foci is constant (2a).

Hyperbola branches are distinct from parabolas and are called hyperbolic arcs.

The transverse axis of a hyperbola has a length of 2a, connecting the vertices.

The relationship between a, b, and c in a hyperbola is given by c squared equals a squared plus b squared.

Hyperbolas have slant asymptotes with equations involving the ratio of a to b or vice versa.

Equation forms for hyperbolas with transverse axes on the x-axis and y-axis.

The Hubble Space Telescope uses hyperbolic mirror systems instead of the standard parabolic mirrors.

Explanation of the Ritchey-Chretien mirror system used in the Hubble Space Telescope, featuring two hyperbolic mirrors.

How hyperbolic mirrors focus light towards the concave side of the second mirror in a system.

The Hubble Space Telescope's main mirror has a focal length of 18 feet, and the secondary mirror 21 feet.

Modeling the Hubble Space Telescope's mirror system using the equations for hyperbolic mirrors.

Calculation of the secondary mirror's equation using the given focal lengths and distances.

The importance of the transverse axis length and its relation to the hyperbola's equation in mirror modeling.

Transcripts

Browse More Related Video

Graphing Conic Sections Part 4: Hyperbolas

Ch. 11.2 Ellipses

INTRODUCTION OF HYPERBOLA || PRE-CALCULUS 2

Ch. 11.1 Parabolas

STANDARD EQUATION OF HYPERBOLA WITH CENTER AT (h, k) || PRE-CALCULUS

Ch. 11.4 Shifted Conics

Related Tags

Hyperbolas Conic Sections Hubble Telescope Mathematics Mirror System Astronomy Foci Distance Transverse Axis Slant Asymptotes Optical Geometry