STANDARD EQUATION OF HYPERBOLA WITH CENTER AT (h, k) || PRE-CALCULUS
TLDRThis educational video tutorial delves into the standard equation of a hyperbola centered at (h, k). It explains the equation's structure, identifying the transverse and conjugate axes, and determining parameters a, b, and c. The lesson outlines how to find vertices, foci, and the lattus rectum, providing step-by-step calculations for a hyperbola with a vertical transverse axis. It also covers an example with a horizontal transverse axis, guiding viewers through the process of graphing hyperbolas on the Cartesian plane and identifying key features such as vertices and foci. The tutorial aims to enhance understanding of hyperbolas and their geometric properties.
Takeaways
- 📚 The video lesson discusses the standard equation of a hyperbola centered at (h, k).
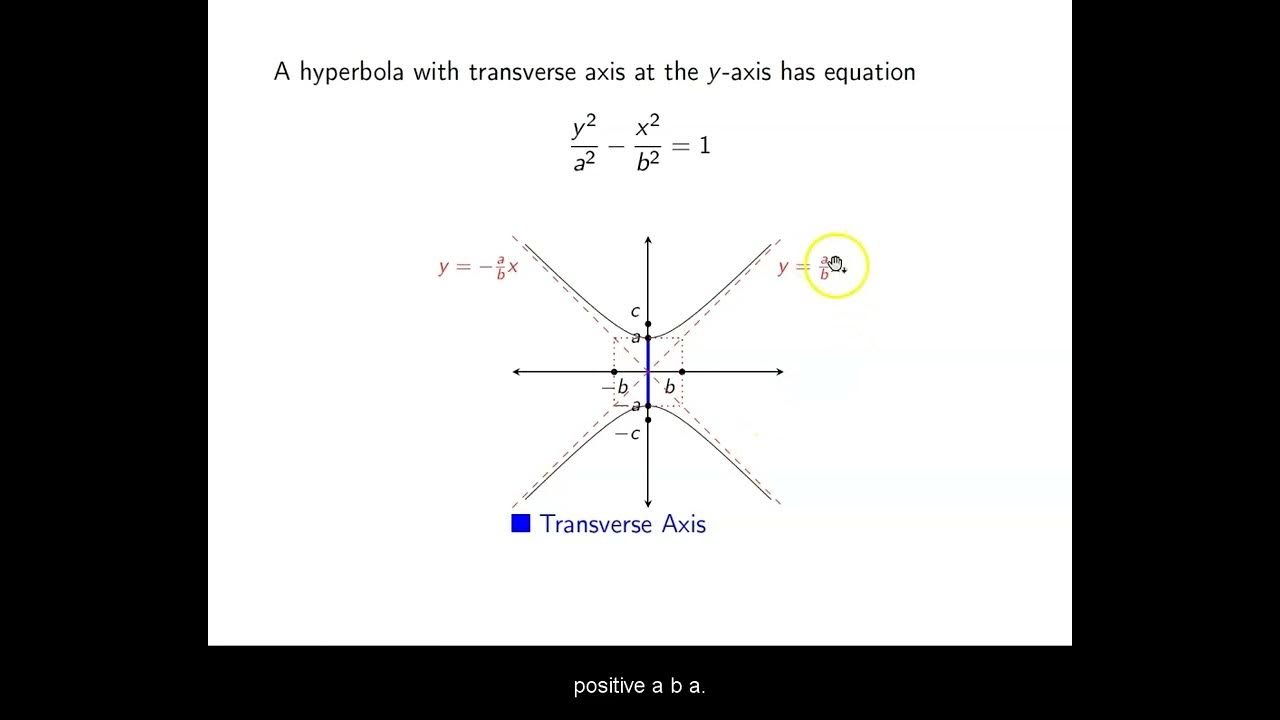
- 📐 The standard form of a hyperbola is \(\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1\).
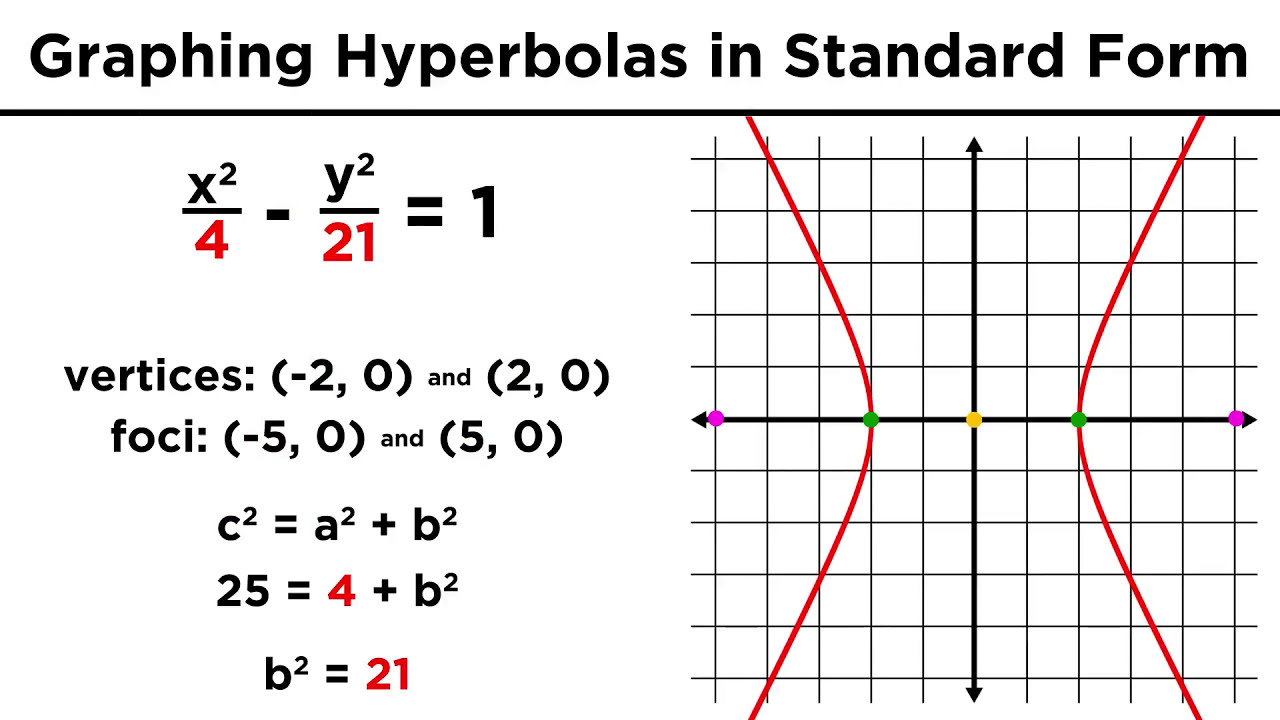
- 🔍 The first example provided has a transverse axis longer than the conjugate axis, with \(a^2 = 16\) and \(b^2 = 9\).
- 📏 The values for \(a\) and \(b\) are calculated as \(a = 4\) and \(b = 3\), with the center of the hyperbola at (3, -2).
- 📍 The distance \(c\) from the center to the foci is calculated using \(c = \sqrt{a^2 + b^2} = 5\).
- 📈 The vertices of the hyperbola are found by adding and subtracting \(a\) and \(b\) from the center coordinates.
- 🔗 The foci are located by adding and subtracting \(c\) from the center coordinates along the transverse axis.
- 📉 The latus rectum is calculated using the formula \(\frac{b^2}{a}\) and is found to be 2.25 for the first example.
- 📝 The second example provided is for a hyperbola with a horizontal transverse axis, with \(a^2 = 4\) and \(b^2 = 12\).
- 📜 The value for \(c\) in the second example is calculated as \(c = \sqrt{a^2 + b^2} = 4\).
- 🖼️ The video concludes with a demonstration of how to plot the hyperbola on the Cartesian plane using the calculated parameters.
Q & A
What is the standard equation of a hyperbola with center at (h, k)?
-The standard equation of a hyperbola with center at (h, k) is given by \(\frac{(y - k)^2}{a^2} - \frac{(x - h)^2}{b^2} = 1\) or \(\frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} = 1\), depending on the orientation of the hyperbola.
What does the equation \(\frac{(y + 2)^2}{16} - \frac{(x - 3)^2}{9} = 1\) represent?
-This equation represents a hyperbola centered at (3, -2) with the transverse axis being the longer axis, and the vertices located at (3 ± 4, -2) and (3, -2 ± 3).
How do you determine the value of 'a' in the hyperbola equation \(\frac{(y + 2)^2}{16} - \frac{(x - 3)^2}{9} = 1\)?
-In the given equation, 'a' is the square root of 16, which is 4, because \(a^2 = 16\).
What is the value of 'b' for the hyperbola equation \(\frac{(y + 2)^2}{16} - \frac{(x - 3)^2}{9} = 1\)?
-The value of 'b' is the square root of 9, which is 3, as \(b^2 = 9\).
How do you calculate the value of 'c' for the hyperbola?
-The value of 'c' is calculated using the formula \(c = \sqrt{a^2 + b^2}\), where 'a' and 'b' are the lengths of the semi-major and semi-minor axes, respectively.
What are the coordinates of the foci for the hyperbola \(\frac{(y + 2)^2}{16} - \frac{(x - 3)^2}{9} = 1\)?
-The foci are located at (3, -2 + 5) and (3, -2 - 5), which simplifies to (3, 3) and (3, -7).
What is the formula for the latus rectum of a hyperbola?
-The formula for the latus rectum of a hyperbola is \(LR = \frac{b^2}{a}\), where 'a' is the distance from the center to a vertex along the transverse axis, and 'b' is the distance from the center to a vertex along the conjugate axis.
How do you find the vertices of a hyperbola given its equation?
-The vertices of a hyperbola can be found by adding and subtracting 'a' from the y-coordinate of the center for a vertical hyperbola, or 'a' from the x-coordinate of the center for a horizontal hyperbola.
What is the orientation of the hyperbola in the equation \(\frac{(x + 2)^2}{4} - \frac{(y + 5)^2}{12} = 1\)?
-The orientation of the hyperbola is horizontal, as indicated by the positive term being associated with the x-coordinate in the equation.
How do you determine the center of the hyperbola from its equation?
-The center of the hyperbola is given by the values of 'h' and 'k' in the equation, which represent the x and y coordinates of the center, respectively.
What are the coordinates of the vertices for the hyperbola \(\frac{(x + 2)^2}{4} - \frac{(y + 5)^2}{12} = 1\)?
-The vertices are located at (-2 ± 2, -5) and (-2, -5 ± √12), which simplifies to (0, -5) and (-2, -5 ± 3.46).
What is the significance of the latus rectum in the context of a hyperbola?
-The latus rectum of a hyperbola is the line segment that passes through the vertex and is perpendicular to the transverse axis, and its length is given by the formula \(LR = \frac{b^2}{a}\).
Outlines
📚 Introduction to Hyperbola Equations
This paragraph introduces the standard equation of a hyperbola centered at (h, k). It explains the equation \(\frac{(y+2)^2}{16} - \frac{(x-3)^2}{9} = 1\) and how it fits into the general form \(\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1\). The speaker identifies the lengths of the transverse and conjugate axes, calculates the values of 'a' and 'b', and determines the center, vertices, and foci of the hyperbola. The explanation includes the calculation of 'c', which represents the distance from the center to a focus, and the coordinates of the vertices and foci are derived from the values of 'a', 'b', and 'c'.
📐 Deriving Hyperbola Parameters and Properties
The second paragraph continues the discussion on hyperbolas, focusing on deriving the parameters 'a', 'b', and 'c', and their geometric interpretations. It outlines the process of finding the vertices and foci coordinates, and introduces the concept of the latus rectum, which is a line segment that passes through the center of the hyperbola and is perpendicular to the transverse axis. The speaker calculates the latus rectum for both the horizontal and vertical orientations of the hyperbola and provides the coordinates for the latus rectum points.
📘 Analyzing a Second Hyperbola Equation
This paragraph presents a new hyperbola equation \(\frac{(x+2)^2}{4} - \frac{(y+5)^2}{12} = 1\) and analyzes it in the context of the standard form. The values of 'a' and 'b' are recalculated, and the process of determining the center, vertices, and foci is repeated. The paragraph also discusses the orientation of the hyperbola and its position in the coordinate plane, highlighting the quadrants where the hyperbola is present.
🔍 Detailed Calculation of Hyperbola's Latus Rectum and Vertices
The fourth paragraph delves deeper into the calculation of the latus rectum and vertices for the second hyperbola equation. It provides a step-by-step process for finding the latus rectum using the formula \(b^2/a\) and identifies the coordinates for the latus rectum points. Additionally, the paragraph discusses the vertices' coordinates and how they relate to the hyperbola's orientation and position on the Cartesian plane.
📚 Graphical Representation of Hyperbolas
In this paragraph, the focus shifts to the graphical representation of hyperbolas. The speaker describes how to plot the hyperbola on the Cartesian plane, including the center, vertices, and the conjugate axis. The paragraph provides a visual understanding of the hyperbola's orientation and its key features, such as the transverse and conjugate axes, and the vertices.
🎓 Conclusion and Invitation for Further Learning
The final paragraph concludes the video lesson by summarizing the key points covered in the tutorial. It includes a brief recap of the hyperbola's properties, such as the center, vertices, and foci, and invites viewers to like, subscribe, and hit the bell button for more video tutorials. The speaker encourages viewers to continue learning and watching more content on the channel.
Mindmap
Keywords
💡Hyperbola
💡Standard Equation
💡Center
💡Transverse Axis
💡Conjugate Axis
💡Vertices
💡Foci
💡Latus Rectum
💡Conic Sections
💡Graphing
Highlights
Introduction to the standard equation of a hyperbola with center at (h, k).
Explanation of the hyperbola's standard equation pattern.
Identification of the transverse axis as longer than the conjugate axis.
Calculation of parameters a, b, and c for the hyperbola's equation.
Determination of the center of the hyperbola using coordinates.
Finding the vertices of the hyperbola by using the values of a and b.
Calculation of the foci of the hyperbola using the value of c.
Introduction of the concept of the latus rectum for hyperbolas.
Explanation of how to find the latus rectum using the formula b^2/a.
Description of the hyperbola's orientation and its relation to the coordinate axes.
Graphical representation of the hyperbola on the Cartesian plane.
Demonstration of how to plot the vertices and foci on the graph.
Calculation of the hyperbola's vertices using the values of a and b.
Determination of the foci coordinates using the value of c.
Illustration of the hyperbola's conjugate axis and transverse axis.
Explanation of how to find the latus rectum points using the formula.
Final summary of the hyperbola's properties and its graph.
Encouragement to like, subscribe, and follow for more educational content.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: