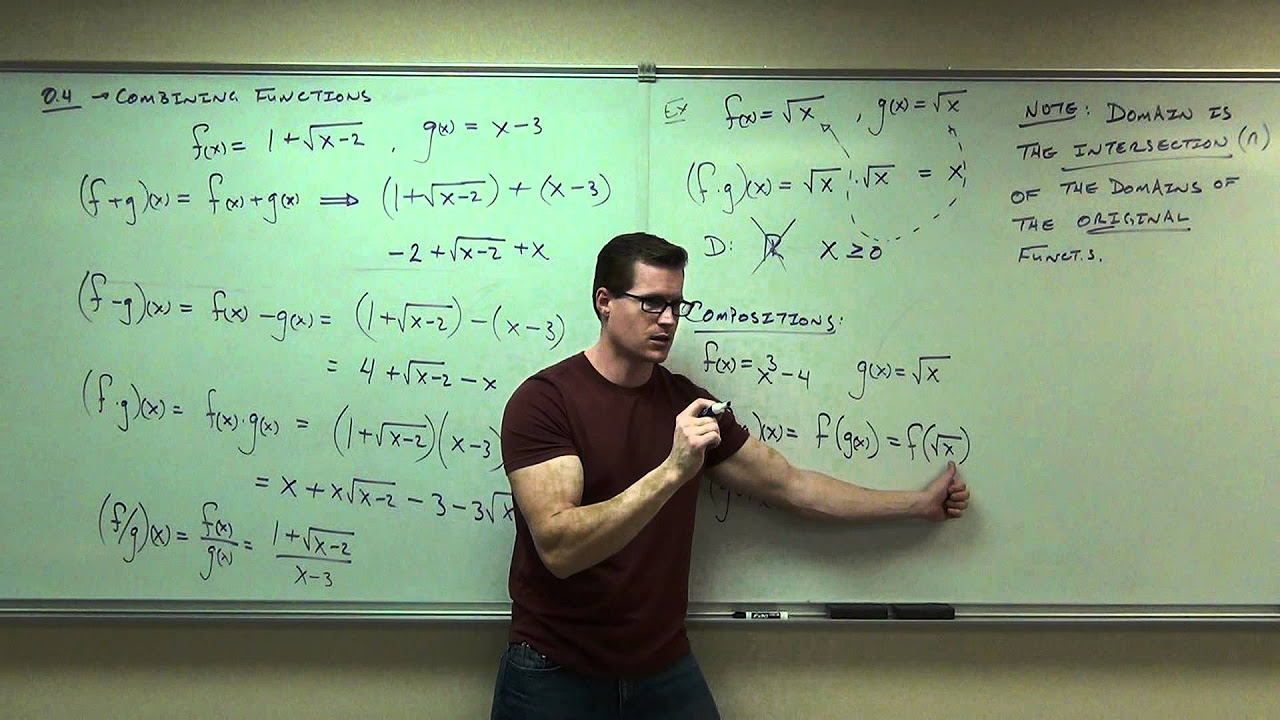Ch. 2.7 Combining Functions

Prof. Williams

24 Aug 202121:27

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of combining and composing functions in algebra. It explains how to create new functions by adding, subtracting, multiplying, and dividing existing ones, emphasizing the importance of domain intersection. The script provides step-by-step examples, illustrating algebraic manipulation, evaluating functions at specific points, and function composition. It also highlights the significance of understanding the graphical and tabular representations of functions, offering a comprehensive approach to mastering algebraic functions.

Takeaways

📚 The lesson covers the concept of combining functions, including addition, subtraction, multiplication, and division of functions, as well as function composition.
🔢 Functions can be combined algebraically, and the domain of the resulting function is the intersection of the domains of the original functions, unless restricted by conditions like division by zero.
➕ When adding or subtracting functions, the new function's domain is the overlapping part of the domains of the two functions involved.
➗ Multiplication and division of functions are similar to arithmetic operations, with division requiring the divisor (function g) not to be zero.
🔑 The process of function composition involves substituting one function into another, moving from right to left, and is read as 'f of g of x'.
📉 The domain of a composite function may be further restricted, especially when dealing with divisions or square roots where certain values are not allowed.
📝 Examples are provided to illustrate how to algebraically combine functions and evaluate them at specific points, emphasizing the importance of correct substitution and order of operations.
📈 The script mentions the importance of understanding function operations not only algebraically but also graphically and through tables of values.
📊 The process of evaluating composite functions is demonstrated both algebraically and through a step-by-step approach using tables of values.
📚 The script concludes with examples of function composition on a graph, showing how to trace the path from input to output through a series of function applications.
🤓 The lesson emphasizes the importance of careful consideration when dealing with function composition, especially in terms of correctly identifying the order of function application and handling domain restrictions.

Q & A

What is the main topic of chapter 2.7?
-The main topic of chapter 2.7 is combining functions, discussing how functions can be added, subtracted, multiplied, and composed.
What is the domain of a new function created by combining two functions?
-The domain of a new function created by combining two functions is the intersection of the domains of the original two functions, meaning the overlapping parts where values are allowed in both functions.
How can you create a new function by adding two functions together?
-A new function can be created by adding two functions together by either adding their outputs or by performing the addition in terms of function notation, ensuring to maintain the correct order of operations with parentheses.
What is the restriction when multiplying two functions to create a new function?
-The restriction when multiplying two functions is that the function you are multiplying by (in this case, g) should not be zero, as this would restrict the domain of the new function.
What is the process of function composition?
-Function composition is the process of taking one function and plugging it into another. It is represented as f(g(x)) and involves substituting the inner function into the outer function from right to left.
How do you find the composition of g(h(f(x)))?
-To find the composition of g(h(f(x))), you start with the innermost function (f(x)), plug its output into the next function (h), and then take the output of h and plug it into the outermost function (g).
What is the domain restriction when dividing two functions?
-The domain restriction when dividing two functions is that the denominator (g in f(g(x))) must not be zero, as division by zero is undefined.
Can you provide an example of adding two functions f(x) = 2x^2 + 1 and g(x) = 2x - 1?
-When adding the functions f(x) = 2x^2 + 1 and g(x) = 2x - 1, you get the new function h(x) = 2x^2 + 2x, after canceling out the +1 and -1.
How would you evaluate f(x) at x = 2 if f(x) = 2x^2 + 1?
-To evaluate f(x) at x = 2, substitute 2 into f(x) to get f(2) = 2*(2)^2 + 1, which simplifies to 2*4 + 1 = 9.
What is the result of the composition of g(h(f(2))) if f(x) = 2x^2 + 1, h(x) = (1/2)x + 1, and g(x) = sqrt(x + 3)?
-The result of the composition g(h(f(2))) with the given functions is g(h(f(2))) = 1/2 * sqrt(22), after evaluating f(2), h(f(2)), and then g(h(f(2))) sequentially.

Outlines

00:00

📚 Introduction to Combining Functions

This paragraph introduces the concept of combining functions, which is the main topic of Chapter 2.7. The speaker explains that functions can be manipulated algebraically, similar to numbers, including addition, subtraction, multiplication, and division. The domain of a new function, resulting from the combination, is the intersection of the domains of the original functions. The paragraph also discusses the process of creating new functions by adding, subtracting, multiplying, and dividing existing functions, while ensuring that the domain restrictions are respected, especially when division by a function that could be zero is involved.

05:01

🔢 Function Composition and Evaluation

The second paragraph delves into the process of evaluating combined functions at specific values and introduces the concept of function composition. It provides an example where two functions, f(x) and g(x), are defined and then combined through addition, subtraction, multiplication, and division to form new functions. The speaker illustrates how to evaluate these new functions at x = 2, emphasizing the equivalence between evaluating the combined function and adding or multiplying the individual function values at that point.

10:01

📈 Visualizing Function Composition

This paragraph continues the discussion on function composition, explaining it visually as 'f eats g which eats h which eats x', emphasizing the left-to-right process of inputting values through a series of functions. The speaker uses an example with three functions, f(x), g(x), and h(x), to demonstrate how to find the composition of g(h(f(x))) step by step, simplifying the expression and eventually evaluating it at a specific value.

15:01

📝 Function Composition Through Tables and Graphs

The fourth paragraph explores different methods of understanding function composition, including algebraic manipulation, tables of values, and graphical representation. It provides an example of how to find compositions like g(h(f(1))) using a table of values, following the input-output sequence through each function. The paragraph also mentions the importance of visualizing the process on a graph to gain a deeper understanding of function behavior.

20:02

📉 Evaluating Compositions Graphically

The final paragraph focuses on evaluating function compositions graphically. It describes a step-by-step process of finding the composition of functions, such as g(h(f(1))) and h(h(h(-3))) by tracing through the graph, starting with an initial input and following the path determined by the outputs of each function until the final output is reached. This visual approach helps to solidify the understanding of how function compositions work and how to interpret them.

Mindmap

Keywords

💡Algebraic Functions

Algebraic functions refer to mathematical expressions that can be represented by variables and operations such as addition, subtraction, multiplication, and division. In the video, the concept is introduced as the basis for understanding how functions can be combined, manipulated, and transformed. For example, the script mentions that 'anything we can do with numbers is what we can do with functions,' highlighting the fundamental role of algebraic functions in the discussion.

💡Domain

The domain of a function is the set of all possible input values (x-values) for which the function is defined. In the context of the video, the domain is crucial when combining functions, as the resulting function's domain is the intersection of the domains of the original functions. The script explains that when creating a new function by combining two, the domain is the overlapping parts of the domains of 'f' and 'g'.

💡Function Composition

Function composition is the process of applying one function to the result of another. It is denoted as f(g(x)) and involves substituting the output of one function as the input for another. The video script discusses this concept in detail, explaining that it requires 'a little bit more brain power' and involves moving 'from right to left,' as in the example of finding g(h(f(x))).

💡Exponents

Exponents are a mathematical notation that represents repeated multiplication of a number by itself a certain number of times. In the script, exponents are mentioned as one of the operations that can be performed with functions, indicating the flexibility and variety of algebraic manipulations possible with functions.

💡Intersection

In mathematics, the intersection refers to a concept where two sets share common elements. In the video, the intersection is used to describe how the domain of a combined function is determined by the common values of the domains of the original functions 'f' and 'g'. The script states that the domain of the new function 'h' is the intersection of 'a' and 'b'.

💡Addition and Subtraction of Functions

The addition and subtraction of functions involve combining two functions by either adding or subtracting their respective outputs. The video script provides examples of how to create a new function 'h' by adding or subtracting functions 'f' and 'g', emphasizing the importance of maintaining the correct order of operations with parentheses.

💡Multiplication and Division of Functions

Multiplication and division of functions are operations where the outputs of two functions are multiplied or divided to create a new function. The video script explains that these operations are similar to multiplying or dividing the outputs of the functions themselves, with the caveat that division by a function that outputs zero is not allowed, as it would restrict the domain.

💡Graphical Representation

Graphical representation in the context of the video refers to visualizing functions and their compositions through graphs. The script mentions thinking about function operations 'more graphically,' suggesting that along with algebraic manipulations, understanding the visual aspect of functions is essential for a comprehensive grasp of the subject.

💡Table of Values

A table of values is a method of representing functions by listing their inputs and corresponding outputs in a tabular format. The video script suggests using a table of values to understand function operations, such as addition, subtraction, multiplication, and division, by directly observing the outputs and how they change with each operation.

💡Evaluation

Evaluation in the context of functions means substituting a specific value into a function to find the corresponding output. The video script provides examples of evaluating functions 'f' and 'g' at specific points, such as f(2) and g(2), to demonstrate how to calculate the output of a function for a given input.

💡Simplification

Simplification in mathematics is the process of making an expression easier to understand or calculate by reducing it to its simplest form. The video script mentions simplification in the context of combining functions, such as pulling out common factors or using distributive properties to make the resulting expressions more manageable.

Highlights

Introduction to combining functions in algebra, emphasizing the ability to perform various operations such as addition, subtraction, multiplication, and exponentiation with functions.

Explanation of function domains and how they intersect to form the domain of a new combined function.

Demonstration of creating a new function 'h' by adding or subtracting two functions 'f' and 'g', with a focus on the importance of domain intersection.

Multiplication and division of functions, with a specific note on the restriction of division by zero.

Example of combining functions algebraically, showing the process of adding, subtracting, multiplying, and dividing functions f(x) and g(x).

Graphical and tabular interpretation of function combination, highlighting the equivalence of algebraic and visual methods.

The concept of function composition, where one function is plugged into another, explained with the notation f(g(x)).

Step-by-step guide on how to perform function composition, emphasizing the left-to-right substitution process.

Example of function composition using f(x) = x^2 - 1, g(x) = sqrt(x + 3), and h(x) = (1/2)x + 1, with a detailed walkthrough.

Simplification of complex compositions and the option to break down the process into smaller steps for clarity.

Evaluating compositions at specific points, such as g(h(f(2))) and its equivalence to g(5/2).

Using tables of values to understand function composition, with an example of tracing inputs and outputs through multiple functions.

Graphical representation of function composition, showing the process of finding g(h(f(1))) on a graph.

The impact of function composition on the domain of the resulting function, especially when dealing with restrictions like division by zero.

Practical application of function composition in various mathematical and real-world scenarios, emphasizing its importance in problem-solving.

Reinforcement of the concept that the output of one function becomes the input for the next in the composition process.

Final summary of the key points covered in the lecture, including the algebraic manipulation and graphical interpretation of function composition.

Transcripts

Browse More Related Video

Calculus AB Homework Day 1 - Review 1: Functions

Algebra/Composition of Functions!

Functions

Calculus 1 Lecture 0.4: Combining and Composition of Functions

Evaluating Functions - Basic Introduction | Algebra

Finding Intersections of Functions (Precaluclus - College Algebra 22)

Related Tags

Function Composition Algebraic Operations Educational Script Mathematics Tutorial Domain Intersection Function Notation Algebraic Functions Graphical Representation Table of Values Composition Example