Transformations, part 2 | Multivariable calculus | Khan Academy
TLDRThis video script delves into the concept of transformations in two-dimensional spaces, illustrating how functions can be visualized as moving points from one plane to another. The presenter animates a specific function, f(x, y) = (x^2 + y^2, x^2 - y^2), to demonstrate the transformation process, using the origin and the point (1,1) as examples. The script emphasizes the conceptual benefits of understanding functions as transformations, particularly for grasping advanced topics in multi-variable calculus and linear algebra, offering a nuanced perspective that complements traditional visualization methods.
Takeaways
- 📚 The video introduces the concept of transformations in the context of functions, which are thought of as moving points from one space to another.
- 📈 The input and output spaces are both two-dimensional, represented as the XY plane, and the video demonstrates how points move within this space.
- 🎥 An animation is used to illustrate the transformation, showing the movement of points, although it's noted that such visualizations are not always available.
- 🔍 The underlying function for the transformation is given by f(x, y) = (x^2 + y^2, x^2 - y^2), which defines how each point in the input space is mapped to the output space.
- 📌 The origin (0,0) is a fixed point under this transformation, meaning it remains unchanged in the output space.
- 🔑 The point (1,1) is used as an example to demonstrate how a point is transformed, moving to the coordinates (2,0).
- 🤔 The video script emphasizes the conceptual understanding of transformations, suggesting that it provides a deeper insight into mathematical functions beyond traditional visualizations.
- 🧠 The importance of understanding transformations is highlighted for grasping more complex mathematical concepts, such as derivatives in multi-variable calculus.
- 🔗 The connection between linear algebra and multi-variable calculus is mentioned, with transformations serving as a bridge between these fields.
- 💡 The script suggests that thinking in terms of transformations can offer a more nuanced understanding of mathematical functions and their properties.
- 📝 While the video uses an animation to aid understanding, the script notes that the concept of transformations is often a mental exercise rather than a visual one.
Q & A
What is the main concept introduced in the video script?
-The main concept introduced in the video script is the idea of transformations in the context of functions, specifically how functions can be thought of as moving points from one space to another in a two-dimensional input and output space.
What is the purpose of visualizing transformations in a two-dimensional space?
-Visualizing transformations in a two-dimensional space helps to understand the underlying function and how it affects the movement of points from the input space to the output space, providing a more intuitive grasp of the function's behavior.
What is the function given in the script for the transformation?
-The function given in the script for the transformation is f(x, y) = (x^2 + y^2, x^2 - y^2), where the first term is the x-component and the second term is the y-component of the output.
What happens to the origin (0,0) under the given transformation?
-Under the given transformation, the origin (0,0) remains fixed because when x and y are both zero, the output is also (0,0), indicating no movement.
How does the point (1,1) transform under the function f(x, y)?
-The point (1,1) transforms to (2,0) under the function f(x, y) because 1^2 + 1^2 equals 2 and 1^2 - 1^2 equals 0.
What is the significance of fixed points in the context of transformations?
-Fixed points are significant in the context of transformations because they represent points that do not move under the transformation, providing a stable reference in the analysis of the function's behavior.
Why is the transformation perspective valuable for understanding multi-variable calculus?
-The transformation perspective is valuable for understanding multi-variable calculus because it offers a more nuanced understanding of concepts like derivatives, allowing for a conceptual grasp of stretching or squishing space that is not as clear with traditional graphs or vector fields.
How does the script suggest thinking about transformations without an animation?
-The script suggests thinking about transformations as a vague thought in the back of one's mind, helping to conceptualize the function's effect on the space without the need for a physical animation.
What is the connection between transformations and linear algebra mentioned in the script?
-The connection between transformations and linear algebra mentioned in the script is that a strong understanding of transformations is crucial for grasping the link between linear algebra and multi-variable calculus when they are studied together.
Why might transformations be a more effective way to visualize certain mathematical concepts?
-Transformations might be a more effective way to visualize certain mathematical concepts because they provide a dynamic perspective that can reveal nuances not as apparent in static visualizations like graphs or vector fields.
What is the potential downside of using transformations to visualize functions?
-The potential downside of using transformations to visualize functions is that it can be confusing due to the many moving parts, and it requires careful observation to follow the movement of individual points.
Outlines
📚 Introduction to Function Transformations
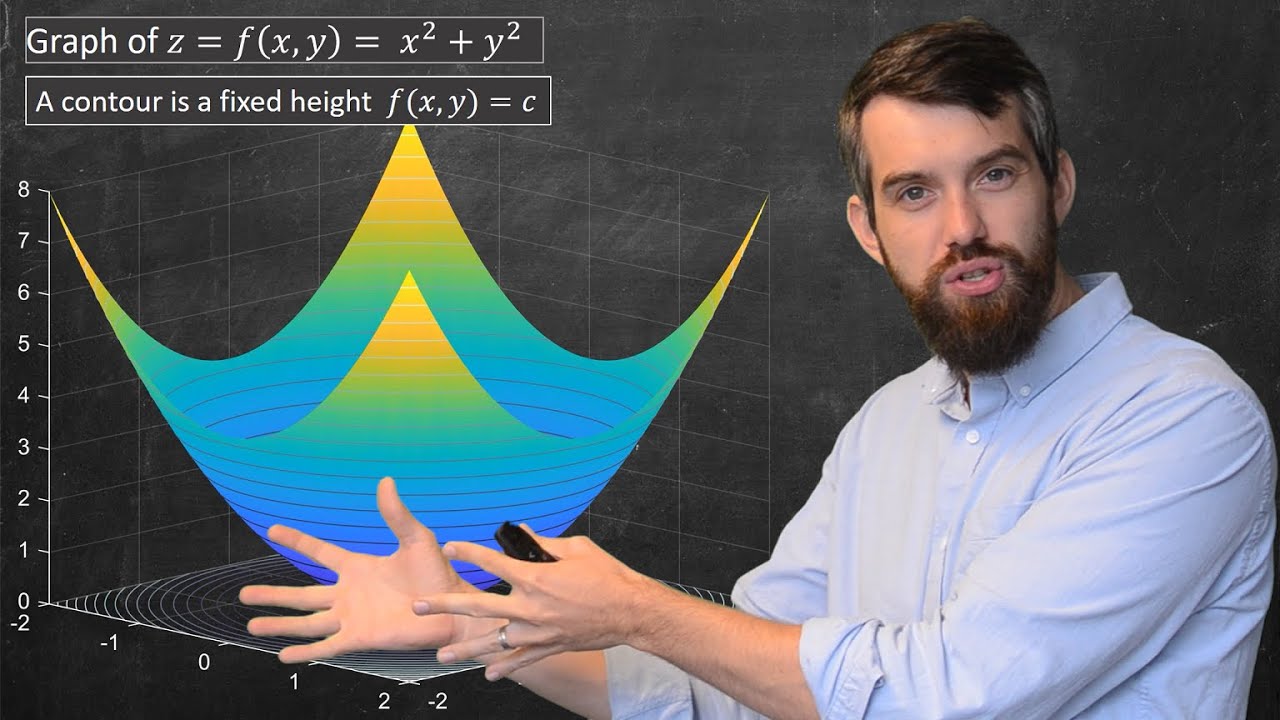
This paragraph introduces the concept of function transformations in a two-dimensional space. The speaker explains that transformations can be visualized as moving points from one space to another, both of which are two-dimensional planes in this example. The video will demonstrate a transformation and then delve into the specifics of the underlying function. The function used in the animation is f(x, y) = (x^2 + y^2, x^2 - y^2), which is a mapping from the input space to the output space. The origin (0,0) is identified as a fixed point, meaning it remains unchanged during the transformation.
🔍 Exploring the Transformation with a Specific Point
The speaker continues by examining the transformation using the point (1,1) as an example. When this point is input into the function, the output is calculated as (2,0), indicating the new location of the point after the transformation. The video is expected to show this movement, although it can be challenging to follow due to the complexity of the animation. The speaker emphasizes the importance of understanding transformations conceptually, as it provides a deeper insight into mathematical concepts such as derivatives and variations in multi-variable calculus, and is crucial for grasping the connections between linear algebra and multi-variable calculus.
Mindmap
Keywords
💡Transformations
💡Input Space
💡Output Space
💡Function
💡XY Plane
💡Origin
💡Fixed Point
💡Derivatives
💡Multi-Variable Calculus
💡Linear Algebra
💡Conceptual Understanding
Highlights
Introduction to transformations and the conceptualization of functions as moving points in a space.
Explanation of input and output spaces as two-dimensional planes for the transformation example.
Demonstration of a transformation with an animated example to visualize the movement of points.
Detailing the underlying function that governs the transformation of points from input to output space.
The function defined as f(x, y) = (x^2 + y^2, x^2 - y^2) for the x and y components of the output respectively.
Illustration of the origin point (0,0) remaining fixed during the transformation, highlighting the concept of a fixed point.
Analysis of the point (1,1) and its transformation outcome to (2,0) in the output space.
Discussion on the difficulty of following complex transformations due to many moving parts.
The importance of understanding transformations conceptually rather than relying solely on animations or manual calculations.
Different visualization methods for functions, such as factor fields and graphs, and their limitations.
The conceptual advantage of thinking in terms of transformations for nuanced understanding in mathematics.
The relevance of transformations to multi-variable calculus and the study of derivatives.
The connection between transformations and linear algebra, and its significance in understanding the relationship between these fields.
The value of having a strong conceptual understanding of transformations for better comprehension in advanced mathematical studies.
The potential for transformations to provide a new perspective or 'color' to one's mathematical understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: