Triple Integrals in Rectangular Coordinates

Houston Math Prep
26 Apr 202016:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video from Houston Math Prep introduces triple integrals in rectangular coordinates, focusing on calculating volumes in three-dimensional space. It explains the concept of a unit volume and how to set up triple integrals with various orders, using the example of finding the volume between the XY plane and a slanted plane. The video also demonstrates how to determine integration bounds and perform the actual integration, illustrating the process with step-by-step examples, including calculating the volume of a solid bounded by planes in the first octant.

Takeaways
  • 📚 The video introduces triple integrals and their application in calculating volumes in rectangular coordinates.
  • 📏 The concept of a unit of volume is explained as a rectangular box with dimensions of length, width, and height.
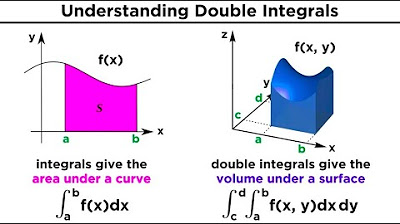
  • 🔍 The script compares double and triple integrals, highlighting the transition from area to volume calculations.
  • 📐 The unit of volume for triple integrals is denoted as 'DV' and can be represented in six different orders due to the three variables involved.
  • 📈 The video demonstrates setting up triple integrals to find the volume between the XY plane and a slanted plane defined by 'z = 6 - 3x - 2y' over a unit square.
  • 📝 The process of finding bounds for triple integrals is explained, emphasizing fixing an 'x, y' value and drawing through in the 'z' direction to determine the limits.
  • 📉 The script provides an example of calculating the volume of a solid bounded by the planes 'z = 4' and 'y = 6 - 3x' in the first octant.
  • ✏️ The importance of the order of integration is stressed, as it determines the sequence of bounds for the variables.
  • 📊 The video explains that without a function inside the integral, the triple integral simplifies to a double integral once the first step is completed.
  • 📌 The concept of including a function within the integral to calculate quantities such as mass, given a density function, is introduced.
  • 🔑 The takeaway emphasizes the importance of understanding the types of quantities calculated by double and triple integrals, such as area, volume, and mass with density functions.
Q & A

  • What is the primary focus of the video by Houston Math Prep?

    -The video focuses on introducing the concept of triple integrals in rectangular coordinates and how they relate to calculating volumes in three-dimensional space.

  • What is the significance of the unit of area 'da' in the context of double integrals?

    -The unit of area 'da' represents a microscopic amount of area in the plane, typically expressed as 'dx dy' or 'dy dx', which is used to calculate the total area of a region by summing these infinitesimally small areas.

  • How does the concept of a unit of volume in triple integrals differ from that of a unit of area in double integrals?

    -The unit of volume in triple integrals is a three-dimensional concept, analogous to the two-dimensional unit of area in double integrals. It considers a small rectangular box with infinitesimal dimensions of 'dx', 'dy', and 'dz' to calculate the volume of a region in 3D space.

  • What is the general form of the unit for volume in a triple integral?

    -The general form of the unit for volume in a triple integral is 'dV', which can be expressed in any order as 'dx dy dz', 'dy dx dz', 'dz dx dy', etc., reflecting the different orders of integration.

  • What does 'D' represent in the context of triple integrals?

    -'D' in triple integrals represents a domain in three-dimensional space, as opposed to 'R' which represents a region in the plane for double integrals.

  • Can you explain the process of setting up the bounds for a triple integral when the order is 'dz dy dx'?

    -To set up the bounds for a triple integral in the order 'dz dy dx', one first integrates with respect to 'z'. This involves fixing values for 'x' and 'y', and determining the bounds for 'z' by considering the entry and exit points of the region in the 3D space, typically the XY plane (z=0) and the top surface defined by an equation.

  • What is the volume calculation example provided in the video involving a slanted plane and a unit square?

    -The example calculates the volume between the XY plane and the slanted plane defined by 'z = 6 - 3x - 2y' above a unit square from 0 to 1 in both the x and y directions.

  • How does the process of finding bounds for a triple integral differ from that of a double integral?

    -In a triple integral, you first fix values for 'x' and 'y' (or other outer variables) and then find the bounds for 'z' (or the inner variable) by considering the region's entry and exit points in the 3D space. In contrast, for a double integral, you fix one variable and find the bounds for the other by considering the region in the plane.

  • What is the significance of the order of integration in triple integrals?

    -The order of integration in triple integrals is significant because it determines the sequence in which you integrate and the bounds you use for each variable. It can affect the complexity of the integral and the method used to find the bounds.

  • Can a triple integral with no function inside it be equivalent to a double integral?

    -Yes, a triple integral with no function inside it, after the first step of integration with respect to 'z', can be equivalent to a double integral, especially when the remaining integral is over a region in the xy-plane.

  • What physical quantity can be calculated using a triple integral with a density function inside it?

    -A triple integral with a density function inside it can be used to calculate the mass of a solid, where each piece of the volume has a different density as defined by the function.

Outlines
00:00
📚 Introduction to Triple Integrals and Rectangular Coordinates

This paragraph introduces the concept of triple integrals in the context of rectangular coordinates, building upon the understanding of double integrals and the unit of area. The analogy of a microscopic box with infinitesimal dimensions to represent volume is used to explain the transition from area to volume. The unit of volume for triple integrals is defined as 'DV', which can be expressed in different orders of differentials (e.g., DX dy DZ, dy DX DZ, etc.). The paragraph also sets the stage for calculating volume in three-dimensional space, using the example of a slanted plane above a unit square to illustrate the setup of a triple integral with the order DZ dy DX.

05:02
📘 Calculating Volume with Triple Integrals: An Example

The second paragraph delves into the process of calculating volume using triple integrals with an example. It explains the setup of the integral with the order DZ dy DX and how to find the bounds for integration. The example involves finding the volume between the XY plane and a slanted plane defined by the equation z = 6 - 3x - 2y, above a unit square. The paragraph outlines the steps to evaluate the integral from the inside out, starting with integrating DZ with respect to z, then dy, and finally DX, emphasizing the importance of maintaining the correct order of integration and evaluating bounds appropriately.

10:02
📙 Triple Integrals for Volume Calculation in a Triangular Region

This paragraph continues the discussion on triple integrals, focusing on calculating the volume of a solid in the first octant bounded by the planes z = 4 and y = 6 - 3x. The explanation includes setting up the triple integral in the order DZ dy DX and determining the bounds for each integration step. The paragraph describes the process of fixing an x and y value to find the z bounds by drawing through the region in the increasing z direction. It also covers the calculation of the remaining bounds for the double integral over the triangular base of the region in the first quadrant, leading to the final volume calculation.

15:03
📒 Applications of Triple Integrals: Volume and Mass Calculation

The final paragraph wraps up the discussion by highlighting the applications of triple integrals in calculating volume and mass within a domain in 3-space. It explains that a triple integral without a function inside calculates the volume of a domain, while including a function represents a density function, allowing for the calculation of mass. The paragraph emphasizes the importance of understanding the types of quantities being calculated and the setup of bounds in rectangular coordinates for triple integrals, providing a comprehensive overview of the topic.

Mindmap
Keywords
💡Triple Integrals
Triple integrals are a mathematical concept used to calculate the volume of a three-dimensional solid or to find the mass of a solid with a given density function. In the video, the concept is introduced as an extension of double integrals, where instead of integrating over an area, the integration is done over a volume. The script uses the example of finding the volume between the XY plane and a slanted plane to illustrate the setup and calculation of triple integrals.
💡Rectangular Coordinates
Rectangular coordinates, also known as Cartesian coordinates, are a system of defining positions in a plane or space using three numbers, typically x, y, and z. In the context of the video, rectangular coordinates are used to set up the bounds for triple integrals and to describe the geometric regions over which the integration is performed.
💡Unit of Area
The unit of area in the script refers to the smallest area element considered when performing a double integral. It is analogous to the concept of a unit volume in triple integrals. The video explains that as more rectangles are packed into an area, the unit of area becomes a microscopic width times a microscopic height, denoted as 'da' in the script.
💡Unit of Volume
The unit of volume is the three-dimensional counterpart to the unit of area. It is used in triple integrals to represent an infinitesimally small volume element, typically a rectangular box with infinitesimal dimensions of x, y, and z. The script explains that as more such boxes are packed into a region in three-dimensional space, the unit of volume becomes 'dv', which can be expressed as dx dy dz or in any order of the variables.
💡Double Integral
A double integral is an integral that extends over a two-dimensional region, such as a plane area. In the video, double integrals are discussed as a precursor to triple integrals, with the unit of area for double integrals being 'da', which can be expressed as dx dy or dy dx. The video uses the concept of double integrals to transition into the explanation of triple integrals.
💡Volume
Volume, in the context of the video, refers to the three-dimensional space occupied by a solid object. The script discusses how to calculate the volume of a solid using triple integrals, especially when the solid is bounded by certain planes or surfaces. The video provides examples of calculating volumes for solids defined by equations of planes.
💡Slanted Plane
A slanted plane in the script refers to a plane that is not perpendicular to the XY plane, which forms the base of the coordinate system. The video uses the equation 'z = 6 - 3x - 2y' to represent a slanted plane that bounds the volume being integrated over. This plane is used to illustrate the process of setting up and evaluating triple integrals.
💡First Octant
The first octant is one of the eight divisions of three-dimensional space, where all coordinates (x, y, z) are positive. In the video, the first octant is used to describe the region where a solid is located, bounded by the planes x = 0, y = 0, and z = 4, as well as the slanted plane y = 6 - 3x.
💡Density Function
A density function in the context of the video is a function that assigns a density value to each point in a volume. When integrated over a volume with a density function, the triple integral calculates the total mass of the solid, assuming the density varies throughout the volume. The script mentions this concept to explain how triple integrals can be used for more than just finding volumes.
💡Mass
Mass, as discussed in the video, is a physical quantity that can be calculated using triple integrals when a density function is included in the integral. It represents the total amount of matter in a solid, taking into account the varying density throughout the volume. The script uses the concept of mass to show an application of triple integrals beyond simple volume calculations.
Highlights

Introduction to triple integrals and rectangular coordinates for calculating volumes in 3D space.

Explanation of the unit of area in rectangular coordinates and its transition to volume in triple integrals.

The concept of a unit volume as a rectangular box with length, width, and height.

Microscopic dimensions of volume in triple integrals represented as DV.

Different orders of integration in triple integrals: DX dy DZ, dy DX DZ, and others.

The distinction between volume of a domain D and area over a region R in integrals.

Setting up triple integrals to find the volume between the XY plane and a slanted plane.

Method of fixing x and y values to determine bounds for the z-integration in a triple integral.

Integration process starting with DZ, followed by dy and DX for a consistent approach.

Example of calculating volume above a unit square bounded by a plane.

Explanation of how to find the bounds for triple integrals in a specific order.

Integration of DZ with respect to z to find the volume of a solid.

Continuation to double integrals after the first step of a triple integral.

Calculation of the volume of a prism in the first octant bounded by planes.

Setting up the bounds for triple integrals when dealing with triangular regions in the first octant.

Integration process for finding the volume of a solid with a density function.

Relating double and triple integrals to physical quantities like volume and mass.

Practical application of triple integrals in calculating volumes and masses in 3D space.

Transcripts

Browse More Related Video

Triple Integrals in Cylindrical Coordinates

Finding Volume with Double Integrals (Rectangular Coordinates)

Lec 25: Triple integrals in rectangular & cylindrical | MIT 18.02 Multivariable Calculus, Fall 2007

Triple Integrals in Spherical Coordinates

Double Integrals in Polar Coordinates

Double and Triple Integrals

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Triple IntegralsVolume CalculationRectangular CoordinatesMathematics EducationArea Under CurveDensity FunctionUnit SquareFirst OctantSlanted Plane3D Space