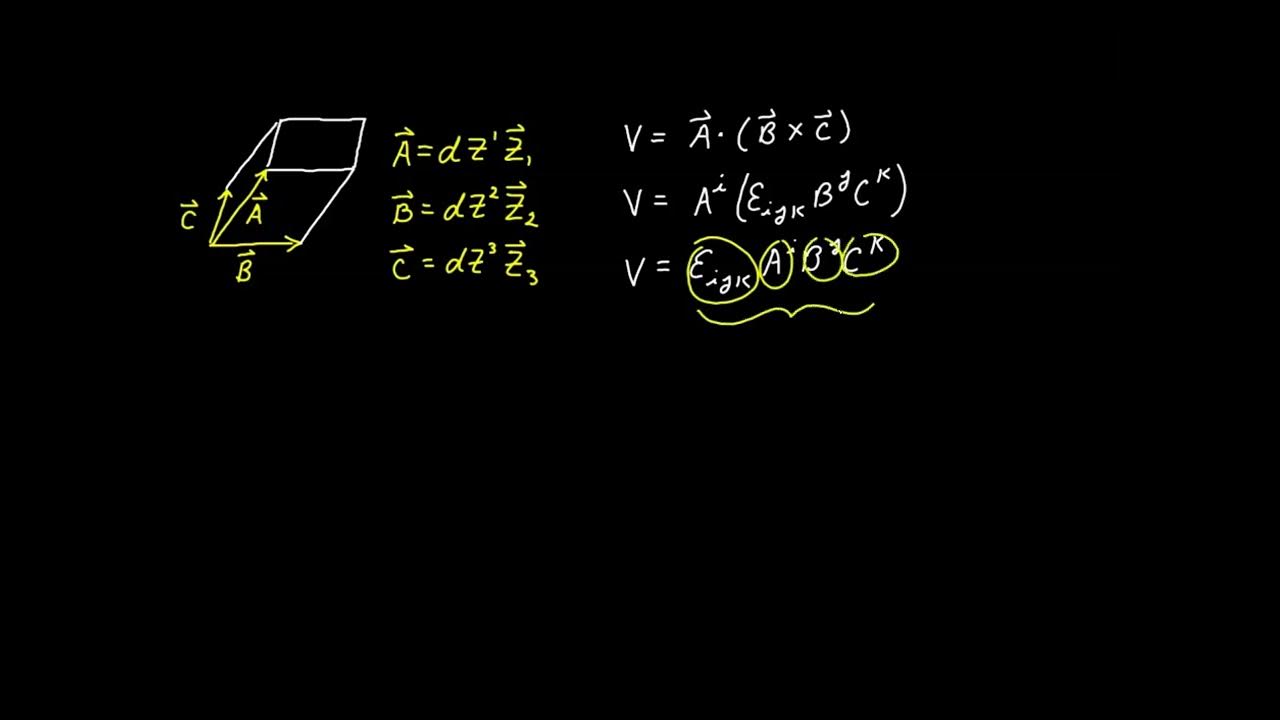Change of Variables & The Jacobian | Multi-variable Integration
TLDRThis video script explores the concept of coordinate system selection for integral calculations, emphasizing the ease of integrating over certain shapes like circles in polar coordinates. It introduces a method to transform a complex region into a simpler one using new variables U and V, demonstrating how to integrate over this new region with clear limits and a Jacobian determinant to adjust for area scaling. The script concludes with an intuitive explanation of the Jacobian, highlighting its role in transforming areas between coordinate systems during integration.
Takeaways
- 📏 The choice of coordinate system for integration is crucial and can simplify the computation process based on the region's geometry.
- 🔄 A change of variables can transform complex regions into simpler ones, making integration easier, such as converting a parallelogram into a rectangle.
- 📚 Cartesian coordinates are straightforward for rectangular regions, while polar coordinates are more suitable for circular regions.
- 🔺 The introduction of new variables U and V can simplify the expression of regions with symmetry that isn't easily captured in Cartesian coordinates.
- 📉 The process of integrating in a new coordinate system involves expressing the original variables (X, Y) in terms of the new variables (U, V) and considering the Jacobian for area scaling.
- 🔄 The Jacobian, represented by J(U, V), is a determinant of a matrix of partial derivatives and serves as a scaling factor for the transformation of areas from the XY to the UV coordinate system.
- ✍️ The formula for changing variables in a double integral involves rewriting the integrand in terms of U and V, adjusting the limits of integration, and multiplying by the Jacobian.
- 🧩 The example given demonstrates how a complex region defined by diagonal lines can be simplified into a rectangle in the UV plane, with the Jacobian being a determinant of a simple matrix.
- 🔍 The Jacobian's intuition is explained through the transformation of a small rectangle in the UV plane into a parallelogram in the XY plane, illustrating the area scaling effect.
- 📝 The video script emphasizes the importance of understanding the Jacobian as a multiplicative factor when integrating over transformed regions.
- 🔑 The video concludes by highlighting the reasons for changing variables in integration, such as simplifying the region or the integrand, and encourages further exploration of multivariable calculus.
Q & A
Why is choosing the right coordinate system important when integrating a function over a region?
-Choosing the right coordinate system is important because it can simplify the integration process. For example, a rectangle is simple to integrate in Cartesian coordinates, while a circle is easier in polar coordinates. The right system can make the region's boundaries and the function to integrate more straightforward to express.
What is the significance of symmetry in the context of choosing a coordinate system for integration?
-Symmetry can greatly simplify the integration process. If a region or the function to be integrated exhibits symmetry, a coordinate system that aligns with this symmetry might make the integration easier by reducing the complexity of the region's boundaries or the integrand.
What is a Jacobian and why is it necessary in the context of changing variables in a multivariable integral?
-A Jacobian is the determinant of a matrix of partial derivatives that represents the scaling factor when transforming areas from one coordinate system to another. It is necessary because it accounts for the change in the area element during the transformation, ensuring the integral is computed correctly in the new coordinate system.
How does the process of changing variables in a single-variable integral compare to multivariable calculus?
-In single-variable calculus, changing variables often involves substituting 'u' for 'x' and adjusting the differential 'dx' to 'du' multiplied by the derivative of 'x' with respect to 'u'. In multivariable calculus, the process is similar but involves two variables, 'u' and 'v', and their corresponding differentials 'du' and 'dv', with the Jacobian serving as the scaling factor.
What is the role of the Jacobian determinant in transforming the area element during a change of variables in a multivariable integral?
-The Jacobian determinant is used to transform the area element 'dA' in the original coordinate system to the new coordinate system. It multiplies the differentials 'du' and 'dv' to give the correct area element in the transformed system, ensuring the integral is scaled properly.
Can you explain the concept of the Jacobian in simpler terms?
-In simpler terms, the Jacobian can be thought of as a 'stretching factor' that tells you how much the area is scaled when you change from one coordinate system to another. It ensures that the integral correctly accounts for this scaling.
What is the purpose of the example provided in the script involving the transformation of a region with diagonal lines?
-The purpose of the example is to illustrate how a change of variables can simplify the integration of a function over a complex region. By introducing new variables 'u' and 'v', the region is transformed into a rectangle, which is easier to integrate over due to its simple boundaries.
How does the choice of new variables 'u' and 'v' in the example simplify the region for integration?
-In the example, 'u' is chosen as 'x - y', and 'v' is chosen as 'y'. This transformation turns the original complex region with diagonal lines into a simple rectangle in the 'uv' plane, where the limits of integration are straightforward horizontal lines.
What are some reasons to perform a change of variables in a multivariable integral?
-Some reasons include simplifying the region of integration, making the integrand easier to work with, or transforming a complex region into a more manageable shape that is easier to integrate over.
What is the intuition behind the Jacobian in the context of transforming a small area from the 'uv' to the 'xy' coordinate system?
-The intuition behind the Jacobian is that when you transform a small rectangle in the 'uv' coordinate system to the 'xy' system, the area of the resulting parallelogram is found by taking the cross product of the vectors representing the changes in 'u' and 'v'. The Jacobian determinant gives this cross product, thus representing the area scaling factor.
Outlines
📚 Choosing the Right Coordinate System for Integration
This paragraph discusses the importance of selecting an appropriate coordinate system for integrating a function over a region. It explains that while Cartesian coordinates are straightforward for rectangular regions, polar coordinates are more suitable for circles. The speaker introduces the concept of changing variables to simplify the integration process, using a region bounded by two horizontal lines and two diagonal lines as an example. By defining new variables U and V, the complex region in the Cartesian plane is transformed into a rectangle in the UV plane, making integration limits straightforward. The paragraph also touches on the general process of changing variables in integration, similar to single-variable substitution, but with the addition of a Jacobian determinant to account for the area scaling factor when changing coordinate systems.
🔍 Detailed Explanation of Multivariable Change of Variables
The second paragraph delves deeper into the process of changing variables in multivariable calculus. It begins by reiterating the need to express the original variables (X and Y) in terms of the new variables (U and V) and vice versa. The speaker then introduces the concept of the Jacobian, a determinant of a matrix of partial derivatives, which serves as a scaling factor when transforming areas from the UV coordinate system back to the XY coordinate system. Using the previously mentioned example, the speaker calculates the Jacobian for the transformation and shows that it simplifies to 1, making the integration in the new coordinate system a straightforward task. The paragraph also discusses the reasons for performing such a transformation, such as simplifying the region of integration or the integrand itself, and concludes with an intuitive explanation of the Jacobian as the determinant of the matrix that results from the transformation of a small rectangle in the UV plane into a parallelogram in the XY plane.
🚀 Wrapping Up the Multivariable Integration Video
In the final paragraph, the speaker wraps up the video by inviting viewers to explore more multivariable calculus videos in a dedicated playlist. This paragraph serves as a conclusion and a call to action, encouraging viewers to continue their mathematical journey by watching additional educational content. It also includes an invitation for viewers to leave comments with any questions they might have about the video's content, fostering a community of learners and mathematicians.
Mindmap
Keywords
💡Integration
💡Coordinate System
💡Rectangular Coordinates
💡Polar Coordinates
💡Change of Variables
💡Jacobian
💡Partial Derivatives
💡Determinant
💡Region of Integration
💡Symmetry
💡Double Integral
Highlights
Integration of functions over a region can be simplified by choosing an appropriate coordinate system.
Rectangles are easy to compute in Cartesian coordinates, while circles are simpler in polar coordinates.
The choice of coordinate system should be based on ease of expression for the region of integration.
A change of variables can transform complex regions into simpler forms, such as turning a parallelogram into a rectangle.
Introducing new variables U and V can simplify the expression of diagonal lines in a region.
The Jacobian, represented as J(U, V), is a scaling factor for the transformation between coordinate systems.
The Jacobian is the determinant of a matrix of partial derivatives, crucial for area scaling during transformations.
The process of integrating in a new coordinate system involves substituting X and Y with functions of U and V.
The limits of integration change with the transformation to the new coordinate system.
The double integral over a region in the original coordinate system is equivalent to the integral over the transformed region.
The Jacobian simplifies to 1 in the example where the transformation is linear and the partial derivatives are constants.
The transformation can be used to simplify both the region and the integrand for easier integration.
The video discusses the intuition behind the Jacobian, relating it to the scaling of areas during coordinate transformations.
A small rectangle in the UV coordinate system transforms into a parallelogram in the XY coordinate system.
The area of the transformed region is found using the cross product of the vectors resulting from the transformation.
The Jacobian represents the multiplicative factor for the area when transforming from UV to XY coordinates.
The video concludes with a playlist of multivariable calculus videos for further exploration of the topic.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: