The Gaussian Integral // Solved Using Polar Coordinates

Dr. Trefor Bazett
26 Jul 202007:51
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the Gaussian integral, a fundamental concept in mathematics with applications in probability and statistics. The integral of e^(-x^2) from negative to positive infinity is intriguing as it surprisingly equals the square root of pi. The presenter demonstrates a creative approach using multi-variable calculus and a change to polar coordinates to simplify and solve the integral. The method leverages the symmetry of the Gaussian function, showcasing the power of coordinate transformations in calculus.

Takeaways
  • πŸ“š The video focuses on solving the Gaussian integral, a fundamental concept in mathematics with applications in probability and statistics.
  • 🎯 The integral of interest is \( \int_{-\infty}^{\infty} e^{-x^2} \, dx \), which surprisingly results in the square root of Ο€, despite no obvious appearance of Ο€ in the integral itself.
  • πŸ€” The Gaussian integral cannot be solved using standard single-variable calculus techniques such as u-substitution or integration by parts.
  • πŸ” The video demonstrates a clever method of squaring the integral to transform it into a double integral, which is then easier to solve using multivariable calculus.
  • πŸ“ˆ The Gaussian function \( e^{-x^2} \) is graphed, showing its common bell-shaped curve, which is prevalent in normal distributions found in various real-world scenarios.
  • πŸ“‰ By changing the variable names within the integral, the video illustrates that the 'dummy' variable can be renamed without affecting the outcome, allowing for a multivariable interpretation.
  • 🌐 The integral is then transformed into a double integral over a two-dimensional space, exploiting the symmetry of the function to simplify the problem.
  • πŸ“ A change of coordinates to polar coordinates is introduced to take advantage of the spherical symmetry of the function, making the integral more tractable.
  • πŸ“ The conversion to polar coordinates involves substituting \( x^2 + y^2 \) with \( r^2 \) and changing the area element from \( dx \, dy \) to \( r \, dr \, d\theta \).
  • πŸŒ€ The limits of integration in polar coordinates are set to cover the entire plane, with \( \theta \) ranging from 0 to \( 2\pi \) and \( r \) from 0 to infinity.
  • πŸ”§ The final step involves a u-substitution in the polar coordinate integral, simplifying the exponential term and allowing for straightforward integration.
  • πŸŽ‰ The result of the double integral is found to be Ο€, and by taking the square root (since the original problem was squared), the Gaussian integral is shown to equal the square root of Ο€.
Q & A

  • What is the Gaussian integral and why is it significant?

    -The Gaussian integral is the integral of the function e to the power of minus x squared over all real numbers from negative infinity to infinity. It is significant because it has applications in various fields such as probability, statistics, and physics, often representing normal distributions found in nature and society.

  • Why does the Gaussian integral include the square root of pi in its result?

    -The inclusion of the square root of pi in the result of the Gaussian integral is due to the mathematical properties of the function and the method of integration. The integral's solution involves a transformation that reveals the pi term, which is a result of the integral's convergence and the function's symmetry.

  • How does the video suggest solving the Gaussian integral?

    -The video suggests solving the Gaussian integral by squaring it and then using multivariable calculus techniques. It involves changing the coordinate system to polar coordinates, which simplifies the integral due to the symmetry of the function.

  • What is the role of multivariable calculus in solving the Gaussian integral?

    -Multivariable calculus plays a crucial role in solving the Gaussian integral by allowing the transformation of the problem into a double integral in polar coordinates. This approach simplifies the integral and makes it solvable, which would not be possible using single-variable calculus techniques alone.

  • Why is the Gaussian function e to the power of minus x squared a common distribution in probability and statistics?

    -The Gaussian function represents a normal distribution, which is a common pattern observed in many natural phenomena and experimental measurements. It is often used to model real-world data, such as the distribution of test scores or heights of a population.

  • What is the significance of the Gaussian integral in the context of normal distributions?

    -The Gaussian integral is significant in the context of normal distributions because it provides a mathematical framework for understanding the properties of these distributions. It helps in calculating probabilities and understanding the spread of data around the mean.

  • What is the process of converting the integral from Cartesian to polar coordinates as described in the video?

    -The process involves recognizing the symmetry of the function and converting the Cartesian coordinates (x, y) to polar coordinates (r, theta). The integral then changes from an integral over dx dy to an integral over r dr d theta, with r representing the radial distance and theta the angle from the origin.

  • How does the video demonstrate the use of polar coordinates to simplify the Gaussian integral?

    -The video demonstrates this by showing that in polar coordinates, the integral's limits of integration naturally cover the entire plane, and the integrand simplifies due to the radial symmetry of the function, making the integral more tractable.

  • What is the final result of the Gaussian integral after applying the method described in the video?

    -The final result of the Gaussian integral, after applying the method described in the video, is the square root of pi. This is obtained by first squaring the integral, solving the resulting double integral in polar coordinates, and then taking the square root of the final result.

  • Why is the Gaussian integral challenging to solve using single-variable calculus techniques?

    -The Gaussian integral is challenging to solve using single-variable calculus techniques because traditional methods such as u-substitution or integration by parts do not apply directly to the function e to the power of minus x squared due to its form and the range of integration over all real numbers.

  • What insight does the video provide about the relationship between the Gaussian integral and the normal distribution?

    -The video provides the insight that the Gaussian integral is not only a mathematical curiosity but also has a direct relationship with the normal distribution, which is a fundamental concept in statistics and probability. The integral's solution helps in understanding the behavior and properties of normal distributions.

Outlines
00:00
πŸ“š Introduction to the Gaussian Integral

This paragraph introduces the Gaussian integral, a mathematical concept integral to understanding certain statistical distributions. The integral of the function e to the power of minus x squared over all real numbers from negative to positive infinity is discussed. The surprising result of this integral being the square root of pi is highlighted, prompting curiosity about its derivation. The Gaussian function's prevalence in probability and statistics, such as in the normal distribution of student grades, is noted. The paragraph sets the stage for a deeper exploration of the integral using multi-variable calculus, which is unconventional for a single-variable problem, and invites the audience to consider why traditional single-variable techniques like substitution or integration by parts do not apply here.

05:00
πŸ” Solving the Gaussian Integral with Multi-variable Calculus

The second paragraph delves into the process of solving the Gaussian integral by leveraging multi-variable calculus. The speaker squares the integral to transform it into a double integral, which is then simplified by changing the variable of integration. The strategy involves recognizing the product of two Gaussian functions as a single function in a multi-variable context. The paragraph explains the transition from Cartesian to polar coordinates, which simplifies the integral due to the spherical symmetry of the function. The conversion to polar coordinates allows for an easier integration by setting u to minus r squared, leading to a straightforward exponential integral. The final step involves evaluating the integral over the new bounds and simplifying the expression to find that the squared integral equals pi. Taking the square root of both sides yields the original Gaussian integral's value as the square root of pi, concluding the video with a demonstration of how multi-variable calculus can elegantly solve what initially seemed to be a challenging single-variable integral.

Mindmap
Keywords
πŸ’‘Gaussian integral
The Gaussian integral is the integral of the function e^(-x^2) over all real numbers, from negative infinity to infinity. This integral is significant because its result is the square root of pi, which is surprising given the lack of any apparent connection to circles or periodic functions. It is used extensively in probability and statistics, representing the normal distribution.
πŸ’‘e^(-x^2)
The function e^(-x^2) is an exponential function with a negative quadratic exponent. This function describes a bell-shaped curve known as the Gaussian or normal distribution in statistics. It is the integrand in the Gaussian integral, and its graph is symmetric around the y-axis, decaying rapidly as x moves away from zero.
πŸ’‘Normal distribution
The normal distribution, often referred to as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. It is represented by the bell-shaped curve of the function e^(-x^2). This distribution is commonly used in statistics and natural and social sciences for real-valued random variables.
πŸ’‘Multivariable calculus
Multivariable calculus involves calculus in more than one variable, such as partial derivatives and multiple integrals. In the video, multivariable calculus is used to solve the Gaussian integral by converting it into a double integral, which simplifies the problem through a change of coordinates.
πŸ’‘Double integral
A double integral is an integral over a two-dimensional area. It is used in the video to convert the Gaussian integral into an easier form to solve. By squaring the integral and introducing a second variable, the problem becomes one of evaluating a double integral, which can be simplified using polar coordinates.
πŸ’‘Polar coordinates
Polar coordinates represent points in the plane using a radius and angle. This coordinate system is useful for integrals with circular symmetry. In the video, the integral is converted from Cartesian to polar coordinates, which simplifies the evaluation of the double integral due to the symmetry of the Gaussian function.
πŸ’‘Symmetry
Symmetry in mathematics refers to a situation where a shape or equation remains unchanged under certain transformations. The Gaussian function e^(-x^2 - y^2) exhibits spherical symmetry, making polar coordinates a natural choice for simplifying the integral. This symmetry helps in solving the Gaussian integral by exploiting the uniformity in all directions.
πŸ’‘Change of coordinates
Change of coordinates involves transforming a problem into a different coordinate system where it may be easier to solve. In the video, the change from Cartesian to polar coordinates simplifies the double integral by taking advantage of the symmetry of the Gaussian function, making the integration process more straightforward.
πŸ’‘Improper integral
An improper integral is an integral with one or more infinite limits or an integrand that approaches infinity at some points within the integration range. The Gaussian integral is an improper integral because it integrates e^(-x^2) from negative infinity to infinity. The video explains how to handle this by transforming it into a solvable form using multivariable calculus.
πŸ’‘Exponential function
An exponential function is a mathematical function of the form e^(ax), where e is the base of the natural logarithm, and a is a constant. In the context of the video, e^(-x^2) is an exponential function that forms the basis of the Gaussian integral. Its properties, such as rapid decay and symmetry, are key to understanding and solving the integral.
Highlights

The video studies the Gaussian integral, an integral of the function e to the minus x squared over all real numbers.

The integral's result is the square root of pi, which is intriguing due to the absence of signs or cosines.

The Gaussian function is extremely common in probability and statistics, often representing normal distributions like student grades.

The video demonstrates solving the integral using multi-variable calculus, rather than single-variable techniques.

The integral is squared to transform it into a double integral, allowing for a multi-variable approach.

The variable names within the integral are interchangeable as they are dummy variables.

The integrand is simplified using exponential rules to combine two exponentials into one.

Polar coordinates are introduced to take advantage of the function's spherical symmetry.

Conversion from Cartesian to polar coordinates is explained, facilitating the integral solution.

The area element in Cartesian coordinates (dx dy) is converted to polar coordinates (r dr dΞΈ).

The limits of integration in polar coordinates cover the entire plane, from 0 to 2Ο€ for ΞΈ and 0 to ∞ for r.

A u-substitution technique is applied with u set to minus r squared, simplifying the integral.

The integral is evaluated with new bounds, simplifying to an exponential function that can be integrated.

The final result of the double integral is pi, which is then used to find the original single integral's value.

The video concludes that the Gaussian integral equals the square root of pi, showcasing the power of coordinate transformation.

The approach of converting a single-variable calculus problem into a multi-variable one is highlighted as innovative.

The video encourages viewers to appreciate the beauty of math by solving challenging integrals.

Transcripts

Browse More Related Video

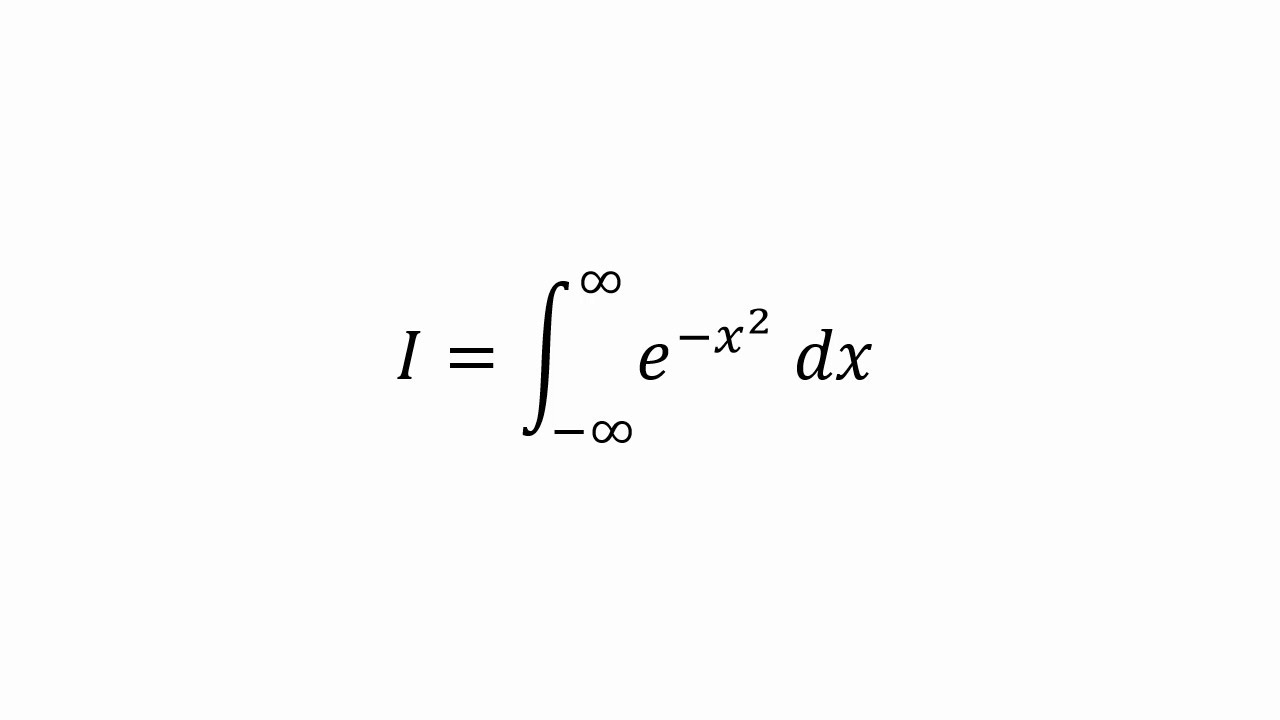
The Gaussian Integral

Applying the Second Fundamental Theorem | MIT 18.01SC Single Variable Calculus, Fall 2010

how Laplace solved the Gaussian integral

Second Fundamental Theorem of Calculus 2nd FTC

Finding a Horizontal Line (y=k) to Divide a Region into Two Equal Parts Using Calculus

Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Gaussian IntegralMulti-variable CalculusMathematicsEducational ContentIntegral TechniquesPolar CoordinatesProbabilityStatisticsNormal DistributionTrigonometry