Perform ANOVA Post-Hoc Tests (Bonferroni Correction) In Excel

Steven Bradburn
23 Feb 202108:01
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial demonstrates how to apply the Bonferroni correction in Excel following a significant one-way ANOVA test. The example uses rabbit body length data from three European regions to illustrate the process of identifying group differences with post-hoc tests. The video guides through performing individual t-tests and adjusting p-values with the Bonferroni method to control for type one errors due to multiple comparisons, concluding which regions' rabbits significantly differ in body length.

Takeaways
  • 📚 The tutorial demonstrates how to perform the Bonferroni correction in Excel following a significant one-way ANOVA result.
  • 🔍 The example involves comparing the body length of rabbits from three different European regions to determine if there are significant differences.
  • 📊 A one-way ANOVA test was conducted, revealing a low p-value indicating significant differences between the average body lengths of the rabbit groups.
  • 🧐 Post-hoc tests are necessary to pinpoint exactly which groups differ significantly from each other.
  • 📝 The tutorial opts for individual Student's t-tests for post-hoc analysis and then corrects for multiple comparisons using the Bonferroni correction.
  • 🔢 The Bonferroni correction is applied by dividing the original alpha level (0.05) by the number of post-hoc tests performed (3 in this case), resulting in a new alpha level of 0.0167.
  • 📉 The p-values from the t-tests are compared against the Bonferroni-corrected alpha level to determine statistical significance.
  • 📋 The IF function in Excel is used to automate the process of determining if a p-value is significant based on the Bonferroni correction.
  • 📝 The final conclusion of the analysis is that rabbits from region 3 have a significantly longer body length compared to those from regions 1 and 2.
  • 👍 The video encourages viewers to like, comment, and subscribe for more tutorials, emphasizing the importance of community engagement.
  • 🔄 The process of replicating the Excel formula for multiple tests is explained, highlighting the use of dollar signs to maintain cell references.
Q & A

  • What is the purpose of the Bonferroni correction in statistical analysis?

    -The Bonferroni correction is used to adjust the alpha level when performing multiple hypothesis tests to reduce the likelihood of Type I errors (false positives). It helps to control the family-wise error rate.

  • What statistical test does the tutorial cover for determining group differences after a significant one-way ANOVA result?

    -The tutorial demonstrates how to perform post-hoc tests using individual Student's t-tests after a significant one-way ANOVA result to determine where the group differences lie.

  • What was the p-value obtained from the one-way ANOVA test in the tutorial example?

    -The p-value from the one-way ANOVA test was very low and below the alpha level of 0.05, indicating a significant difference between the means of the groups.

  • How many rabbits were measured from each region in the example provided in the tutorial?

    -In the example, 15 rabbits were measured from each of the three different regions in Europe.

  • What is the formula used in Excel to perform a two-sample t-test with equal variances and two tails?

    -The formula used in Excel for a two-sample t-test with equal variances and two tails is: `=TTEST(range1, range2, 2, 2)`.

  • How many post-hoc tests are performed in the example provided in the script?

    -Three post-hoc tests are performed in the example: comparing region 1 to region 2, region 2 to region 3, and region 3 to region 1.

  • What is the Bonferroni-corrected alpha level if the original alpha level is 0.05 and three post-hoc tests are performed?

    -The Bonferroni-corrected alpha level is 0.05 divided by 3, which equals 0.0167.

  • How can you determine if a p-value is significant after applying the Bonferroni correction in Excel?

    -You can use the IF function in Excel to compare the p-value with the Bonferroni-corrected alpha level and return 'Yes' if the p-value is less than or equal to the corrected alpha level, and 'No' otherwise.

  • What does the '$' symbol do when used in the IF function formula in Excel?

    -The '$' symbol is used to create an absolute reference to the cell containing the Bonferroni-corrected alpha level, ensuring that the cell reference does not change when the formula is copied down.

  • What conclusion can be drawn from the post-hoc analyses with the Bonferroni correction in the tutorial example?

    -The conclusion is that the rabbits in region 3 were significantly longer in body length compared with the rabbits from regions 2 and 1, after performing the one-way ANOVA test and post-hoc analyses with the Bonferroni correction.

Outlines
00:00
📊 Performing Bonferroni Correction Post One-Way ANOVA

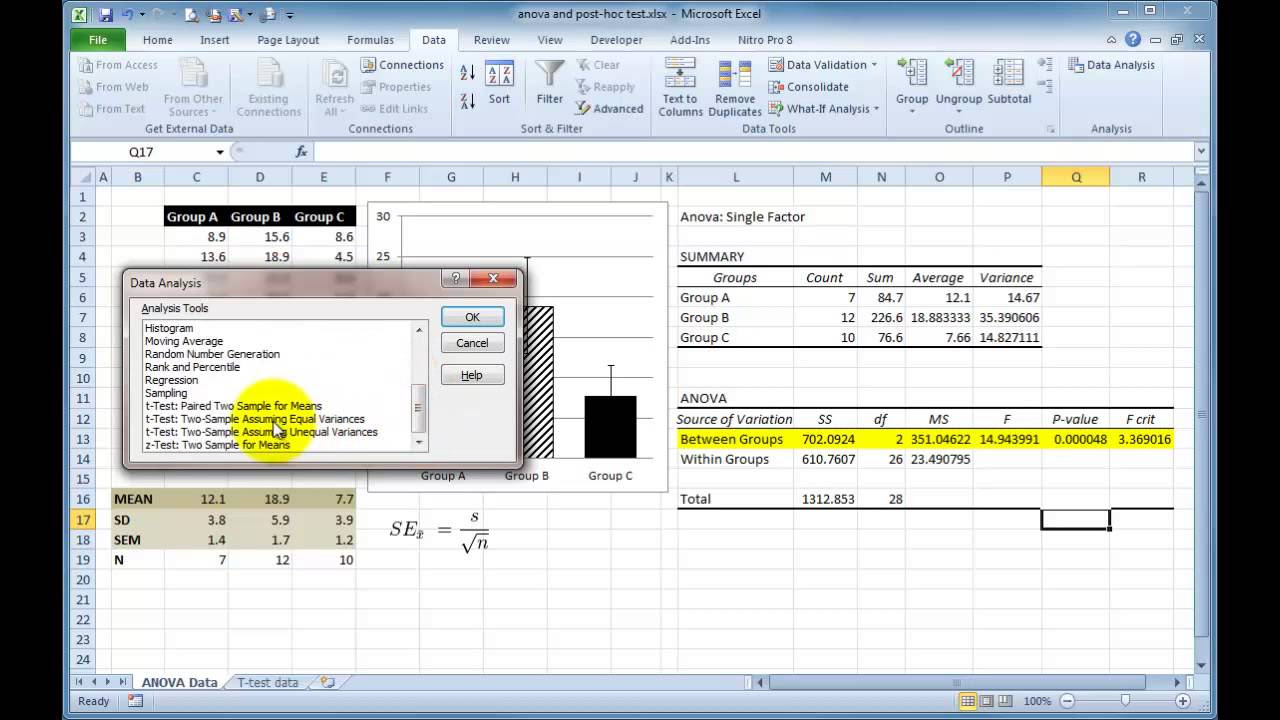
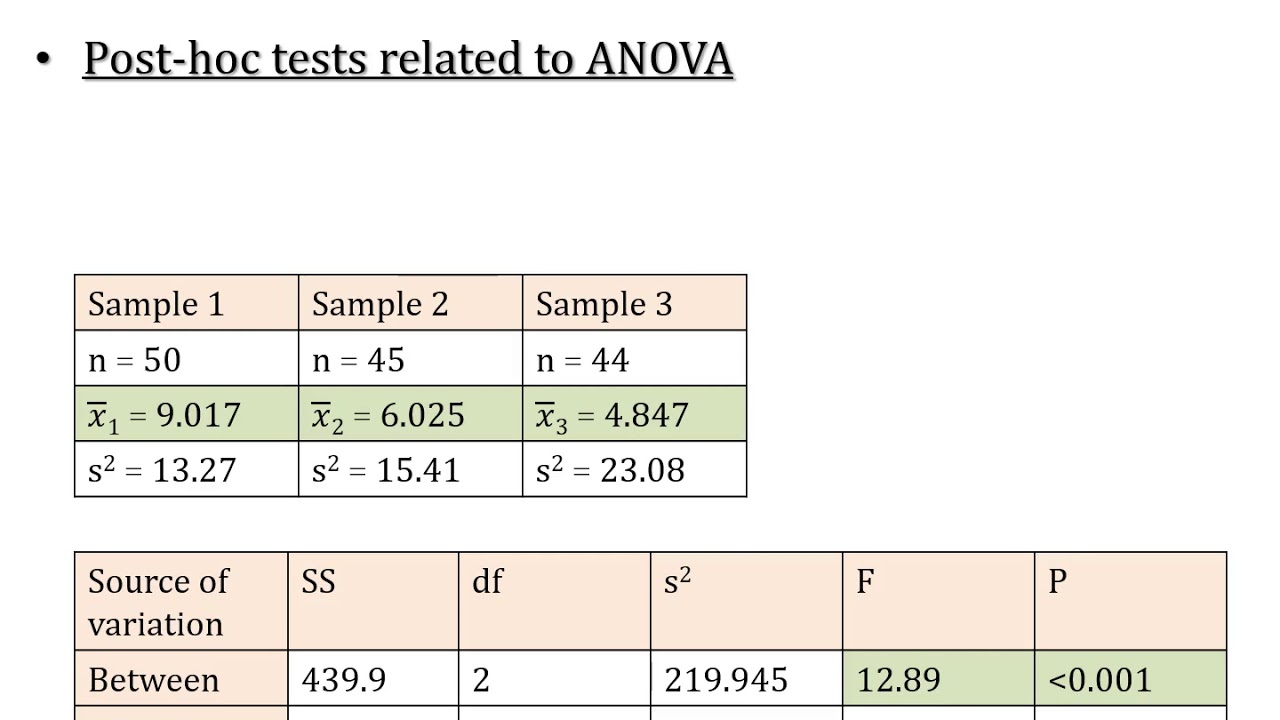
This paragraph introduces a tutorial on applying the Bonferroni correction in Excel after a significant one-way ANOVA result. The speaker explains the context of the tutorial, which involves comparing the body lengths of rabbits from three European regions. The initial ANOVA test revealed significant differences between the groups, prompting the need for post-hoc tests to pinpoint where these differences lie. The tutorial suggests using individual Student's t-tests for each possible group comparison and then correcting for multiple comparisons using the Bonferroni method. The speaker also mentions a previous tutorial for those unfamiliar with the ANOVA test and its interpretation in Excel.

05:00
📘 Conducting Post-Hoc Tests and Applying Bonferroni Correction

The second paragraph delves into the specifics of conducting post-hoc tests using Student's t-tests for each group comparison and then applying the Bonferroni correction to adjust the alpha level for multiple hypotheses testing. The speaker demonstrates how to perform a two-sample t-test in Excel and emphasizes the importance of the Bonferroni correction to reduce the risk of type I errors due to multiple testing. The tutorial provides a step-by-step guide on calculating the Bonferroni-corrected alpha level and using Excel's IF function to automatically determine the significance of each post-hoc test result. The speaker concludes by summarizing the findings from the rabbit body length study, indicating that region 3's rabbits were significantly longer than those from regions 1 and 2 after the Bonferroni correction.

Mindmap
Keywords
💡Bonferroni Correction
The Bonferroni Correction is a statistical method used to adjust the significance levels of multiple hypothesis tests to reduce the likelihood of type I errors (false positives). In the video, it is used following a significant one-way ANOVA result to determine the significance of pairwise group comparisons. The script mentions dividing the original alpha level of 0.05 by the number of post-hoc tests (3 in this case) to get a Bonferroni-corrected alpha level of 0.0167.
💡One-Way ANOVA
One-Way ANOVA (Analysis of Variance) is a statistical test used to compare the means of three or more independent groups to determine if there are any significant differences between them. In the video, it is used to analyze the body length measurements of rabbits from three different European regions. The script indicates that the p-value from the one-way ANOVA was below the alpha level of 0.05, suggesting significant differences between the groups.
💡Post-Hoc Tests
Post-hoc tests are used after an ANOVA to determine where the significant differences between group means lie. The video script describes performing individual Student's t-tests as a form of post-hoc analysis and then correcting for multiple comparisons using the Bonferroni method. The script mentions comparing each region to the others to identify specific group differences.
💡Student's t-test
Student's t-test is a statistical method used to compare the means of two groups to determine if there is a significant difference between them. In the video, it is used for pairwise comparisons of the rabbit body length data from different regions after a significant ANOVA result. The script provides a detailed step-by-step guide on how to perform a two-sample t-test in Excel.
💡P-Value
A p-value is the probability that the observed results of a statistical test occurred by chance if the null hypothesis were true. In the video, p-values from the one-way ANOVA and subsequent t-tests are used to determine significance. The script explains that a p-value less than the alpha level indicates a significant result, and after Bonferroni correction, a p-value less than 0.0167 is considered significant.
💡Alpha Level
The alpha level is the threshold for statistical significance in a hypothesis test, often set at 0.05. In the video, the original alpha level is 0.05 for the one-way ANOVA, and it is adjusted using the Bonferroni correction for multiple comparisons, resulting in a new alpha level of 0.0167.
💡Type I Error
A type I error occurs when a true null hypothesis is incorrectly rejected. The script mentions the Bonferroni correction as a way to reduce the chance of a type I error by adjusting the alpha level when performing multiple hypothesis tests.
💡Excel
Excel is a spreadsheet program used for data organization, analysis, and calculations. The video script provides a tutorial on how to use Excel for statistical tests like the one-way ANOVA, t-tests, and the Bonferroni correction. The script includes step-by-step instructions for performing these tests within Excel.
💡Multiple Comparisons
Multiple comparisons refer to the practice of conducting multiple statistical tests on the same set of data, which increases the risk of type I errors. The script discusses the use of the Bonferroni correction to adjust for this risk when performing post-hoc tests after a significant ANOVA result.
💡Significance
In statistics, significance refers to the likelihood that the observed results are not due to chance. The video script uses the terms 'significant' and 'not significant' to describe the results of the statistical tests, with the Bonferroni correction helping to determine the adjusted threshold for significance.
💡IF Function
The IF function in Excel is a logical test that returns one value if a condition is met and another value if it is not. In the video, the IF function is used to automatically determine if a p-value is less than or equal to the Bonferroni-corrected alpha level, indicating significance.
Highlights

Tutorial demonstrates the Bonferroni correction in Excel following a significant one-way ANOVA.

The example uses rabbit body length measurements from three different European regions.

A one-way ANOVA test reveals significant differences between the average rabbit body lengths of the regions.

Post-hoc tests are necessary to determine which specific groups are significantly different.

The tutorial recommends performing individual Student t-tests for each group comparison.

The Bonferroni correction is introduced to adjust for multiple comparisons.

The original alpha level of 0.05 is divided by the number of post-hoc tests to apply the Bonferroni correction.

Excel formulas are used to calculate the Bonferroni-corrected alpha level.

The p-values from the t-tests are compared against the Bonferroni-corrected alpha level to determine significance.

Excel's IF function is used to automatically determine the significance of post-hoc tests.

The use of dollar signs in Excel formulas ensures the Bonferroni-corrected alpha level remains constant when formulas are copied.

The final analysis concludes that rabbits in region 3 have a significantly longer body length compared to regions 1 and 2.

The tutorial emphasizes the importance of the Bonferroni correction to avoid false positives in multiple hypothesis testing.

The video provides a step-by-step guide on performing Student t-tests in Excel.

The tutorial offers a brief overview of the one-way ANOVA test for context.

The video is part of a series on statistical tests in Excel, with a previous tutorial on one-way ANOVA.

The tutorial encourages viewers to subscribe for more weekly statistical tutorials.

Transcripts

Browse More Related Video

Performing a One-way ANOVA in Excel with post-hoc t-tests

One-way ANOVA & Post-Hoc Analysis in Excel

How To... Perform a One-Way ANOVA Test in SPSS

LSD; Least Significant Difference; Post Hoc Test of ANOVA; Comparison of Means (Part A)

How to do a One-Way ANOVA in SPSS (12-6)

Duncan Multiple Range Test (DMRT) with Compact Letter Display

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Bonferroni CorrectionExcel TutorialStatistical AnalysisANOVA TestPost-hoc TestsData InterpretationMultiple ComparisonsStudent T-TestSignificance TestingResearch Methodology