Measure of Central Tendency of Grouped Data for beginners

Oninab (Educational) Resources
14 Mar 202118:38
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial video guides beginners through calculating the mean, median, and mode for grouped data in statistics. It demonstrates the process step-by-step, starting with determining the mid-value of class intervals, then multiplying these by their respective frequencies to find the mean. The median is calculated by identifying the median class and applying a specific formula. Lastly, the mode is found by analyzing the class with the highest frequency and using a formula that involves differences in frequencies and class widths. The video concludes with a clear explanation of each step, ensuring viewers can apply these concepts to their own data analysis.

Takeaways
  • 📊 The tutorial is focused on explaining the calculation of mean, median, and mode for grouped data in statistics.
  • 🔢 To calculate the mean, the formula used is the sum of the product of frequency (f) and mid-value (x) divided by the total frequency.
  • 📈 The mid-value (x) for each class interval is found by adding the lower and upper class limits and dividing by 2.
  • 📚 The script provides a step-by-step example of calculating the mean, including creating a column for mid-values and the FX product.
  • 📉 To find the median, the formula involves the lower class boundary of the median class, adjusted by the cumulative frequency and class width.
  • 📝 Cumulative frequency is calculated by summing the frequencies of all preceding class intervals.
  • 🔎 The median class is identified by finding the class interval where the cumulative frequency first exceeds half of the total frequency.
  • 📋 The mode is calculated by determining the class with the highest frequency and using a formula that adjusts the lower class boundary based on differences in frequencies of adjacent classes.
  • 📉 The class width is the same for each interval in this example, simplifying the calculation of the median and mode.
  • 📌 The tutorial includes a detailed example with calculations for each step, providing clarity on how to approach grouped data statistics.
  • 👍 The presenter encourages viewers to like, share, and subscribe to the YouTube channel for more educational content.
Q & A

  • What is the main topic of the tutorial video?

    -The main topic of the tutorial video is statistics, specifically focusing on calculating the mean, median, and mode of grouped data for beginners.

  • What is the formula used to calculate the mean of grouped data?

    -The formula used to calculate the mean of grouped data is the sum of the product of frequency (f) and mid-value (x), divided by the sum of the frequencies (Σfx / Σf).

  • How is the mid-value (x) of a class interval determined?

    -The mid-value (x) of a class interval is determined by adding the lower and upper class limits and dividing by 2.

  • What does the term 'FX' represent in the context of the video?

    -In the context of the video, 'FX' represents the product of the frequency (f) and the mid-value (x) of a class interval.

  • What is the median class in the context of calculating the median?

    -The median class is the class interval that contains the value which is exactly in the middle of the dataset when ordered by frequency.

  • How is the lower class boundary of the first class interval calculated?

    -The lower class boundary of the first class interval is calculated by taking the mid-value between the assumed lower limit (1) and the actual lower limit of the first interval (11), which is (1+11)/2 = 6.

  • What is the formula for calculating the median of grouped data?

    -The formula for calculating the median of grouped data involves the lower class boundary of the median class, the cumulative frequency, the frequency of the median class, and the class width.

  • What is the purpose of calculating the cumulative frequency?

    -The purpose of calculating the cumulative frequency is to determine the total number of observations up to a certain class interval, which is crucial for finding the median class.

  • How is the mode of the grouped data calculated?

    -The mode is calculated by finding the class interval with the highest frequency, then using the lower class boundary of that class, along with the differences in frequencies (Δ1 and Δ2) and the class width to determine the exact mode.

  • What is the difference between Δ1 and Δ2 in the mode calculation formula?

    -Δ1 is the positive difference between the frequency of the modal class and the class before it, while Δ2 is the positive difference between the frequency of the modal class and the class after it.

Outlines
00:00
📊 Introduction to Grouped Data Statistics

This paragraph introduces a tutorial on statistics, focusing on calculating the mean, median, and mode for grouped data. It explains the initial setup, including the frequency and age range columns, and the process of calculating the mean by creating additional columns for the mid-value of each class interval. The tutorial demonstrates the calculation of the mid-values for different age groups, such as 11-20, 21-30, and so on, up to 71-80, and then proceeds to the calculation of the FX column, which is the product of frequency and mid-value for each class interval.

05:01
🧮 Calculating the Mean and Median

The paragraph continues with the calculation of the mean by summing up the FX column and dividing by the total frequency, resulting in the mean age of the distribution. It then moves on to the calculation of the median, introducing the formula and explaining the need for additional columns for lower class boundaries and cumulative frequency. The process involves identifying the median class based on the cumulative frequency and calculating the median using the lower class boundary, the cumulative frequency before the median class, and the class width.

10:02
📈 Determining the Lower Class Boundaries and Cumulative Frequencies

This section delves into the specifics of determining the lower class boundaries for each interval and calculating the cumulative frequencies. It explains how to find the lower boundary for the first class interval and subsequent intervals by averaging the upper and lower bounds of the intervals. The paragraph also details the creation of the cumulative frequency column, starting from an assumed interval before the first class with a frequency of zero, and incrementally adding the frequencies of each class interval to find the cumulative total.

15:05
📊 Finding the Median and Mode of the Distribution

The final paragraph concludes the tutorial by calculating the median and mode of the data distribution. It describes how to find the median class by dividing the total frequency by two and identifying the class interval with a cumulative frequency just greater than this value. The median is then calculated using the formula provided, taking into account the lower class boundary, the frequency before the median class, and the class width. The paragraph also explains how to determine the mode by identifying the class with the highest frequency, calculating the differences between frequencies of adjacent classes, and applying the mode formula to find the modal value.

Mindmap
Keywords
💡Statistics
Statistics is the discipline that concerns the collection, analysis, interpretation, presentation, and organization of data. In the context of this video, statistics is the overarching theme, focusing on the analysis of grouped data to understand the central tendencies of a dataset. The script discusses the calculation of mean, median, and mode, which are key statistical measures.
💡Mean
Mean, often referred to as the average, is a measure of central tendency in statistics. It is calculated by summing all the values in a dataset and then dividing by the number of values. The script provides a step-by-step guide on calculating the mean of grouped data, using the formula \( \text{Mean} = \frac{\sum (F \times X)}{\sum F} \), where \( F \) is the frequency and \( X \) is the mid-value of the class intervals.
💡Median
Median is another measure of central tendency, which is the middle value of a dataset when it is ordered from least to greatest. If the number of data points is odd, the median is the middle number; if even, it is the average of the two middle numbers. The script explains how to calculate the median for grouped data using a specific formula that involves the lower class boundary, cumulative frequency, and class width.
💡Mode
Mode is the value that appears most frequently in a dataset and is used to represent the most common value within the data. The script describes the process of identifying the modal class interval, which is the class with the highest frequency, and then calculating the mode using the lower class boundary, differences between frequencies of adjacent classes, and the class width.
💡Grouped Data
Grouped data is a way of organizing numerical data into groups or intervals. It is often used when dealing with large datasets to simplify the analysis. The video script demonstrates the process of analyzing grouped data by calculating the mean, median, and mode from a table that includes age ranges and their corresponding frequencies.
💡Class Interval
A class interval, also known as a bin, is a range of values that groups data into manageable segments. In the script, class intervals are used to represent age ranges, such as 11-20, 21-30, etc. The calculation of the mid-value of each class interval is crucial for determining the mean of the grouped data.
💡Frequency
Frequency refers to the number of occurrences of a particular value or range of values in a dataset. In the context of the video, frequency is the number of individuals falling within each age range. The script shows how to use frequency to calculate the mean and median by multiplying it with the mid-value of the class intervals.
💡Mid-Value
The mid-value of a class interval is the average of the lower and upper bounds of the interval. It is used as a representative value for the data points within that interval. The script demonstrates how to calculate the mid-value for each class interval and then use it in the calculation of the mean.
💡Cumulative Frequency
Cumulative frequency is the total number of data points up to and including a particular class interval. The script explains how to calculate the cumulative frequency by adding the frequency of each class interval to the sum of the frequencies of all previous intervals, which is essential for determining the median.
💡Class Width
Class width is the difference between the upper and lower bounds of a class interval. It represents the size of each group in the dataset. In the script, the class width is consistently 10 for each age range and is used in the calculation of the median and mode.
Highlights

Introduction to a tutorial on statistics focusing on mean, median, and mode for grouped data beginners.

Explanation of the formula for calculating the mean using the summation of frequency times the mid-value (FX) divided by the total frequency (F).

Demonstration of finding the mid-value for each class interval by averaging the lower and upper class limits.

Step-by-step calculation of the mid-value for the age groups 11-20, 21-30, and so on, up to 71-80.

Creation of an FX column to multiply the frequency by the mid-value for each class interval.

Summation of the FX column and the frequency column to calculate the mean of the distribution.

Introduction of the median calculation process for grouped data.

Explanation of the median formula involving the lower class boundary, cumulative frequency, and class width.

Calculation of the lower class boundary for each interval, including the interval before the first class.

Creation of a cumulative frequency column to assist in finding the median class.

Identification of the median class based on the cumulative frequency greater than half the total frequency.

Calculation of the median using the lower class boundary of the median class, the cumulative frequency before, and the class width.

Introduction to the mode calculation for grouped data.

Explanation of the mode formula involving the lower class boundary of the modal class, differences in frequency (Delta 1 and Delta 2), and class width.

Identification of the modal class as the one with the highest frequency.

Calculation of Delta 1 and Delta 2 to find the mode using the provided formula.

Final calculation of the mode as 43, representing the most frequent age group in the distribution.

Conclusion of the tutorial with an invitation to like, share, and subscribe for more content.

Transcripts

Browse More Related Video

Mean, Median and Mode of Grouped Data(Lesson 2)

Mean, median and mode of grouped Data(Lesson 1)

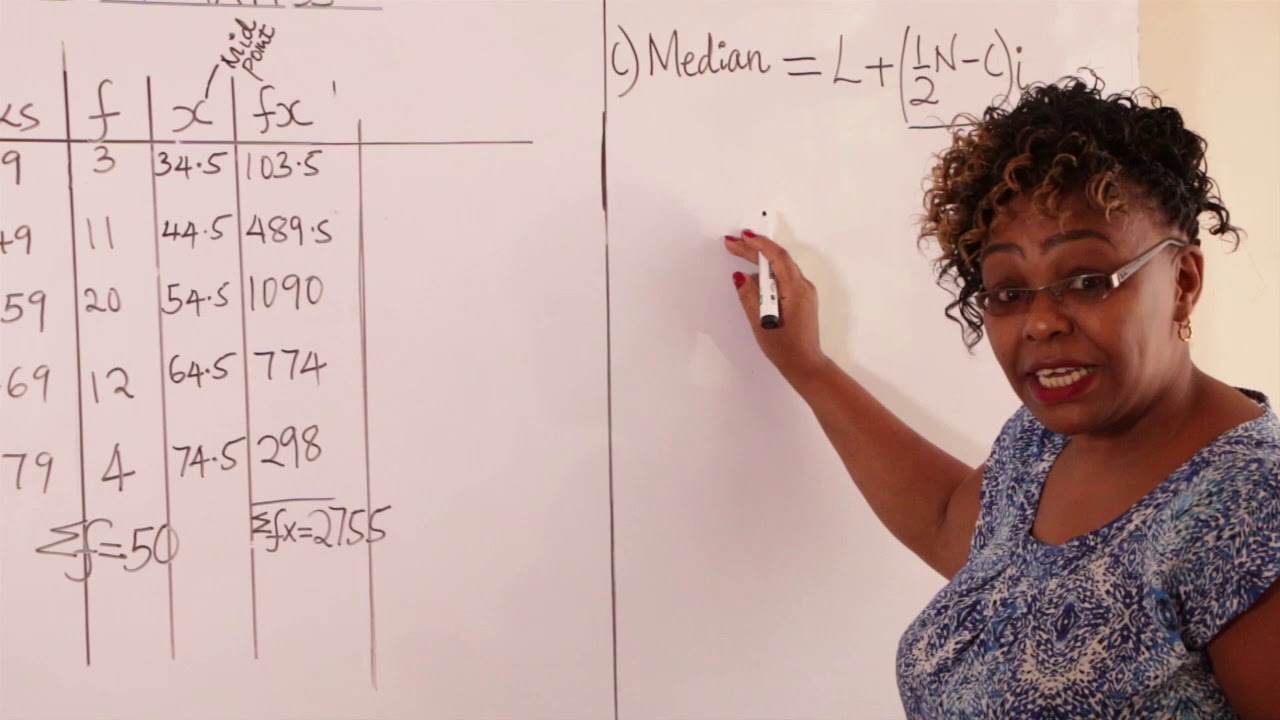
FORM 2 MATHS STATISTICS I MEAN,MODE & MEDIAN

Measures of Central Tendency (Grouped Data) | Basic Statistics

Statistics - Mean, Median & Mode for a grouped frequency data

Statistics of Grouped Data: Mean, Median and Mode

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistics TutorialMean CalculationMedian FindingMode DeterminationGrouped DataBeginners GuideData AnalysisNumerical MethodsEducational VideoMathematicsDescriptive Statistics