The Probability an Elevator is Overloaded Central Limit Theorem with StatCrunch

The Math Sorcerer
7 Sept 201804:10
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a probability problem involving an elevator with a maximum capacity of 1,650 pounds or 10 passengers. It calculates the probability of the elevator being overloaded with 10 adult males, assuming their weights are normally distributed with a mean of 167 pounds and a standard deviation of 25. The standard deviation of the sample mean is derived and used in a normal distribution calculation to find the probability of the mean weight exceeding 165 pounds. The result suggests a high risk of overload, indicating the elevator may not be safe.

Takeaways
  • 📝 The elevator placard indicates a maximum capacity of 1,650 pounds or 10 passengers, with a mean weight limit of 165 pounds per person.
  • 🔢 The sample size 'n' in the problem is 10, representing the number of adult male passengers the elevator can hold.
  • 🤔 The problem asks to find the probability that the elevator is overloaded, which is when the mean weight of the passengers, denoted as X̄, exceeds 165 pounds.
  • 📊 It's assumed that the weights of the males follow a normal distribution with a mean (μ) of 167 pounds and a standard deviation (σ) of 25 pounds.
  • 🧮 The standard deviation of the sample mean (σ/√n) is calculated to be approximately 7.9056, using the formula for standard deviation of the mean.
  • 📉 To find the probability of the elevator being overloaded, the normal distribution calculator is used with the parameters μ=167 and the calculated standard deviation.
  • 📝 The calculator is set to provide a high level of precision, using many decimal places to ensure accuracy in the result.
  • 🔎 The normal distribution calculator is used to find the probability that the mean weight exceeds 165 pounds, with the result being approximately 0.5999.
  • 🤨 The result suggests that there is nearly a 60% chance that the elevator will be overloaded, indicating a safety concern.
  • 🚫 Based on the calculated probability, the conclusion is that the elevator may not be safe, as there is a high likelihood of it being overloaded with 10 passengers.
  • 💡 The script emphasizes the importance of using a high number of decimal places when dealing with statistical calculations to avoid errors.
Q & A

  • What is the maximum weight capacity of the elevator?

    -The maximum weight capacity of the elevator is 1,650 pounds.

  • What is the maximum number of passengers the elevator can hold?

    -The elevator can hold a maximum of 10 passengers.

  • What is the mean weight per passenger to ensure the elevator is not overloaded?

    -The mean weight per passenger should be up to 165 pounds to ensure the elevator is not overloaded.

  • What is the sample size (n) in this problem?

    -The sample size (n) is 10, which corresponds to the 10 passengers.

  • What is the population mean weight (μ) of males assumed in this problem?

    -The population mean weight (μ) of males is assumed to be 167 pounds.

  • What is the population standard deviation (σ) of males' weights?

    -The population standard deviation (σ) of males' weights is 25 pounds.

  • How do you calculate the standard deviation of the sample mean (X̄)?

    -The standard deviation of the sample mean (X̄) is calculated by dividing the population standard deviation (σ) by the square root of the sample size (n). In this case, it is 25 divided by the square root of 10.

  • What is the calculated standard deviation of the sample mean?

    -The calculated standard deviation of the sample mean is approximately 7.90569.

  • What probability is being calculated in this problem?

    -The probability being calculated is that the mean weight of the 10 passengers (X̄) is greater than 165 pounds, which would mean the elevator is overloaded.

  • What is the probability that the elevator is overloaded with 10 passengers?

    -The probability that the elevator is overloaded with 10 passengers is approximately 0.5999 or 59.99%.

  • Does the elevator appear to be safe based on the calculated probability?

    -No, the elevator does not appear to be safe because there is almost a 60% chance that the elevator will be overloaded with 10 passengers.

Outlines
00:00
🚫 Elevator Overload Probability Calculation

The script discusses an elevator with a maximum capacity of 1,650 pounds or 10 passengers. It poses a probability problem to determine the likelihood of the elevator being overloaded, assuming 10 adult male passengers with an average weight exceeding 165 pounds. The weights are normally distributed with a mean (mu) of 167 pounds and a standard deviation (sigma) of 25 pounds. The script explains the process of calculating the new standard deviation for the sample mean (X-bar), which is sigma divided by the square root of the sample size (n), resulting in 7.9056. Using this value, the script then demonstrates how to calculate the probability of the elevator being overloaded with StatCrunch software, concluding with a probability of approximately 0.5999, indicating a high risk of overload.

Mindmap
Keywords
💡Maximum Capacity
Maximum capacity refers to the highest weight or number of passengers an elevator can safely handle, which is 1,650 pounds or 10 passengers in this context. It sets the limit to prevent the elevator from being overloaded, ensuring safety. For this elevator, if the combined weight of 10 passengers exceeds this limit, it is considered overloaded.
💡Mean Weight
Mean weight is the average weight of a group of people. In this script, it is used to assess whether the average weight of 10 adult male passengers exceeds 165 pounds, which would indicate the elevator is overloaded. The elevator's safety is evaluated by comparing the passengers' mean weight to this threshold.
💡Probability
Probability, in this context, measures the likelihood that the mean weight of 10 passengers exceeds the elevator's capacity. The script calculates this probability to determine the risk of the elevator being overloaded. A high probability (around 60%) suggests that the elevator is often overloaded, indicating a safety concern.
💡Normal Distribution
Normal distribution is a statistical concept where values are symmetrically distributed around the mean, forming a bell-shaped curve. The weights of adult males are assumed to follow this distribution, with a mean (μ) of 167 pounds and a standard deviation (σ) of 25 pounds. This assumption allows for the calculation of the probability that the elevator will be overloaded.
💡Standard Deviation
Standard deviation (σ) measures the amount of variation or dispersion in a set of values. Here, it quantifies the variability of individual weights around the mean weight of 167 pounds. A standard deviation of 25 pounds helps calculate the standard deviation of the sample mean, which is crucial for determining the elevator's safety.
💡Sample Size (n)
Sample size (n) refers to the number of passengers considered, which is 10 in this scenario. It impacts the calculation of the standard deviation of the sample mean. The larger the sample size, the smaller the standard error, which refines the probability calculation of the elevator being overloaded.
💡Sample Mean (X̄)
Sample mean (X̄) is the average weight of the passengers in the sample, used to evaluate if the elevator is overloaded. It’s compared against the threshold of 165 pounds. If the sample mean exceeds this value, the elevator is considered overloaded. This comparison helps assess the elevator’s operational safety.
💡Population Mean (μ)
Population mean (μ) is the average weight of all adult males in the population, which is 167 pounds. It serves as a reference point for evaluating the sample mean. This comparison helps in determining the probability of overloading when 10 passengers are in the elevator, assuming their weights follow the normal distribution centered around this mean.
💡Standard Error
Standard error is the standard deviation of the sample mean, calculated as the population standard deviation divided by the square root of the sample size. In this script, it quantifies the expected variability of the sample mean, which is 7.906 pounds. It’s essential for calculating the probability that the elevator will exceed its weight limit.
💡Safety Evaluation
Safety evaluation involves assessing whether the elevator can operate safely under specified conditions. Here, it’s based on the probability that the elevator is overloaded. With a 60% chance of the mean weight exceeding the safe threshold, the elevator is deemed unsafe, indicating a significant risk for the passengers.
Highlights

An elevator has a placard stating that the maximum capacity is 1,650 pounds or 10 passengers.

The mean weight per passenger is calculated to be up to 165 pounds for 10 passengers.

Sample size (n) is given as 10 for this problem.

We need to find the probability that the elevator is overloaded if the mean weight exceeds 165 pounds.

Assume the weights of males are normally distributed with a mean (μ) of 167 pounds.

The standard deviation (σ) of the population is 25 pounds.

We need to compute the standard deviation of the sample mean (X̄), which is σ divided by the square root of n.

The standard deviation of the sample mean is calculated as 25 divided by the square root of 10, approximately 7.90569.

It is suggested to use many decimals in calculations to avoid errors in the final result.

Using the normal distribution calculator to find the probability that X̄ is greater than 165.

Inputting the mean of 167 and the standard deviation of approximately 7.90569 into the calculator.

The probability that the mean weight exceeds 165 pounds is approximately 0.5999.

Rounding the result to four decimal places gives 0.5999.

There is almost a 60% chance that the elevator will be overloaded with 10 passengers.

Conclusion: The elevator does not appear to be safe since there is a high probability of overloading.

Transcripts

Browse More Related Video

Calculating Probabilities of Sample Distributions with StatCrunch

Math 14 HW 6.4.11-T Using the Central Limit Theorem

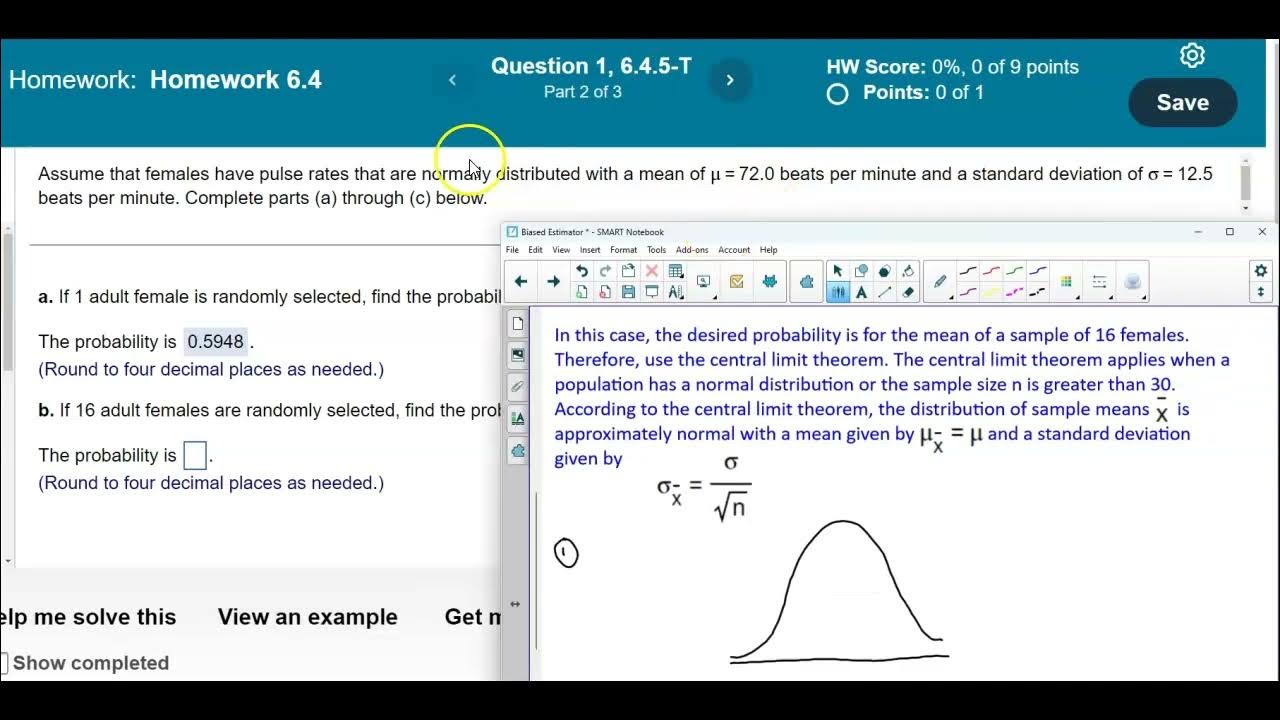
Math 14 HW 6.4.5-T Using the Central Limit Theorem

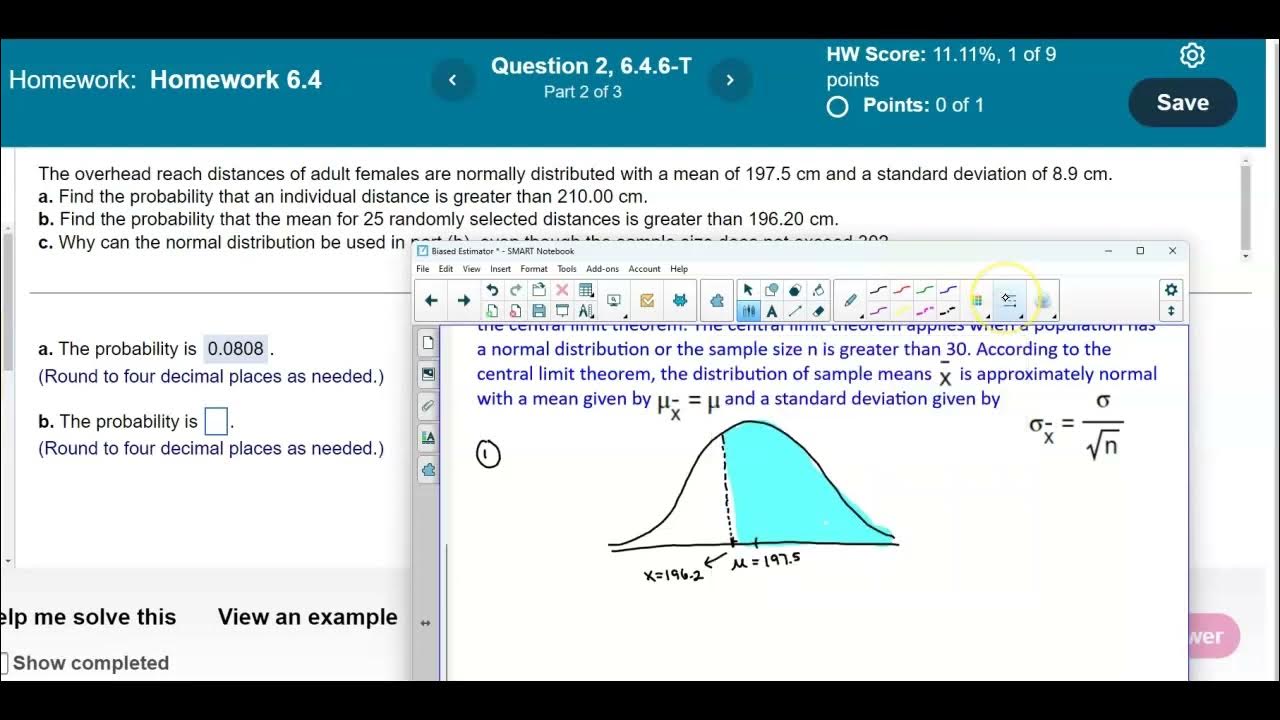
Math 14 HW 6.4.6-T Using the Central Limit Theorem

Math 14 HW 6.4.12-T Using the Central Limit Theorem

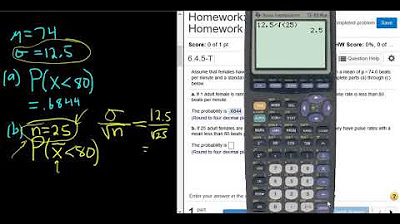
Central Limit Theorem Probability Question with Pulse Rates in StatCrunch

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Elevator SafetyStatistical AnalysisPassenger WeightsNormal DistributionSample SizeMean WeightStandard DeviationProbability CalculationRisk AssessmentSafety StandardsStatistical Tools