Math 119 Chap 8 part 2

Brad Bolton

14 Dec 202066:47

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is a detailed instructional guide on hypothesis testing in statistics, focusing on chapters eight and nine. It covers testing claims about population proportions, means, and standard deviations using both calculators and manual calculations. The instructor demonstrates step-by-step processes, including setting up null and alternate hypotheses, determining test criteria, calculating test statistics, and interpreting p-values to make conclusions about the validity of claims. The script emphasizes the importance of understanding the concepts behind the calculations, not just relying on technology.

Takeaways

📚 The instructor is covering Chapter 8 of a statistics course, focusing on hypothesis testing, particularly for proportions and means.
🔢 The class is learning to use a calculator to assist with hypothesis testing, specifically for test statistics and p-values.
📉 The script explains the process of setting up null and alternative hypotheses, emphasizing the importance of identifying the correct claim and its opposite.
📌 The video demonstrates how to identify the type of tail test (left-tailed, right-tailed, or two-tailed) based on the alternative hypothesis.
🎯 The instructor shows step-by-step calculations for test statistics using both manual methods and calculator functions, such as '1 prop Z test' for proportions.
🧩 The importance of understanding the difference between null and alternative hypotheses is highlighted, with the null hypothesis always having an equal sign.
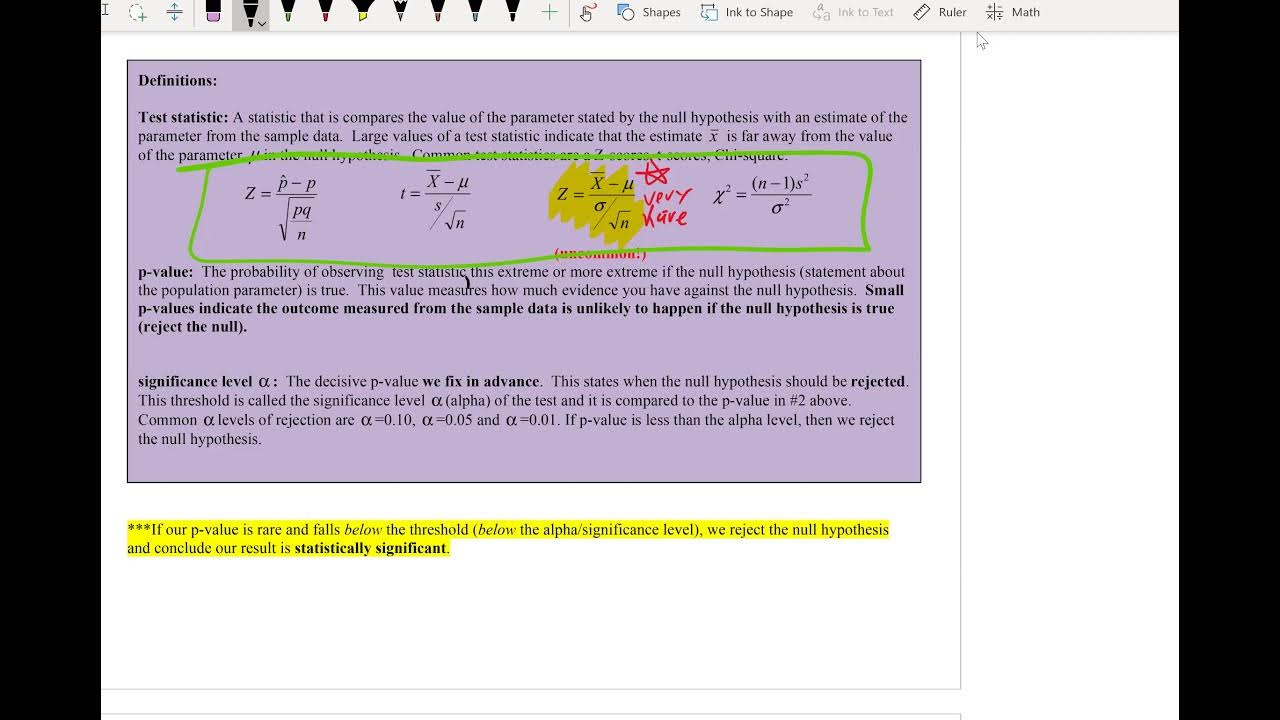
📝 The script covers the concept of p-values and their role in hypothesis testing, explaining how to compare p-values to the significance level (alpha) to make a decision.
🤔 The instructor discusses the concept of failing to reject the null hypothesis, which means there is insufficient evidence to support the alternative hypothesis, rather than proving the null hypothesis true.
📈 The video includes examples of hypothesis testing for population means, using sample data to test claims about the average values in a population.
📊 The process of calculating chi-squared test statistics for hypothesis testing involving standard deviations is explained, including the use of the chi-squared distribution.
🔍 The script emphasizes the importance of understanding the steps of hypothesis testing, which can be applied to various statistical scenarios including proportions, means, and standard deviations.

Q & A

What is the main topic of the video?
-The main topic of the video is teaching how to conduct hypothesis testing for population proportions, means, and standard deviations using both calculator functions and manual calculations.
What are the key steps involved in hypothesis testing as discussed in the video?
-The key steps involved in hypothesis testing, as discussed in the video, include stating the null and alternate hypotheses, determining the type of test (z-test, t-test, chi-squared test), calculating the test statistic, determining the p-value, making a decision based on the p-value compared to the significance level (alpha), and drawing a conclusion.
What is the difference between a null hypothesis and an alternate hypothesis?
-The null hypothesis (denoted as H0) is a statement of no effect or no difference, often including an equality sign (e.g., µ = 18). The alternate hypothesis (H1 or Ha) is what you might believe to be true, and it does not contain an equality sign (e.g., µ ≠ 18).
What is the significance of the alpha level in hypothesis testing?
-The alpha level (commonly denoted as α) is the probability of rejecting the null hypothesis when it is true. It represents the threshold for deciding whether the results of a test are statistically significant. If the p-value is less than or equal to α, the null hypothesis is rejected.
What is a p-value in the context of hypothesis testing?
-The p-value is the probability of observing the test results (or something more extreme) assuming that the null hypothesis is true. A smaller p-value indicates strong evidence against the null hypothesis.
How does the video instructor suggest using a calculator for hypothesis testing?
-The video instructor suggests using specific calculator functions such as '1 prop z test' for proportion tests, 't-test' for mean tests, and 'chi-squared cdf' for testing standard deviations. The calculator can compute the test statistic and p-value, streamlining the process.
What is the difference between a one-tailed and a two-tailed test?
-A one-tailed test is used when the alternate hypothesis predicts a difference in a specific direction (e.g., greater than or less than). A two-tailed test is used when the alternate hypothesis predicts a difference in any direction (e.g., not equal to).
Why is it necessary to double the p-value in certain situations?
-The p-value needs to be doubled in two-tailed tests because the critical region is split between the two tails of the distribution. This adjustment ensures that the total probability of making a Type I error does not exceed the chosen alpha level.
What does the video script imply about the importance of understanding the steps of hypothesis testing?
-The video script implies that understanding the steps of hypothesis testing is crucial for correctly applying statistical methods, interpreting results, and making informed decisions based on data, especially when using calculators or software that may obscure the underlying process.
Can you provide an example of a hypothesis test for a population mean from the video?
-An example from the video is testing whether adults in America spend a different average number of hours per week on leisure activities than the previously claimed 18 hours. The researcher took a random sample of 10 adults and calculated the sample mean and standard deviation to perform a hypothesis test.

Outlines

00:00

📚 Introduction to Chapter 8 Hypothesis Testing

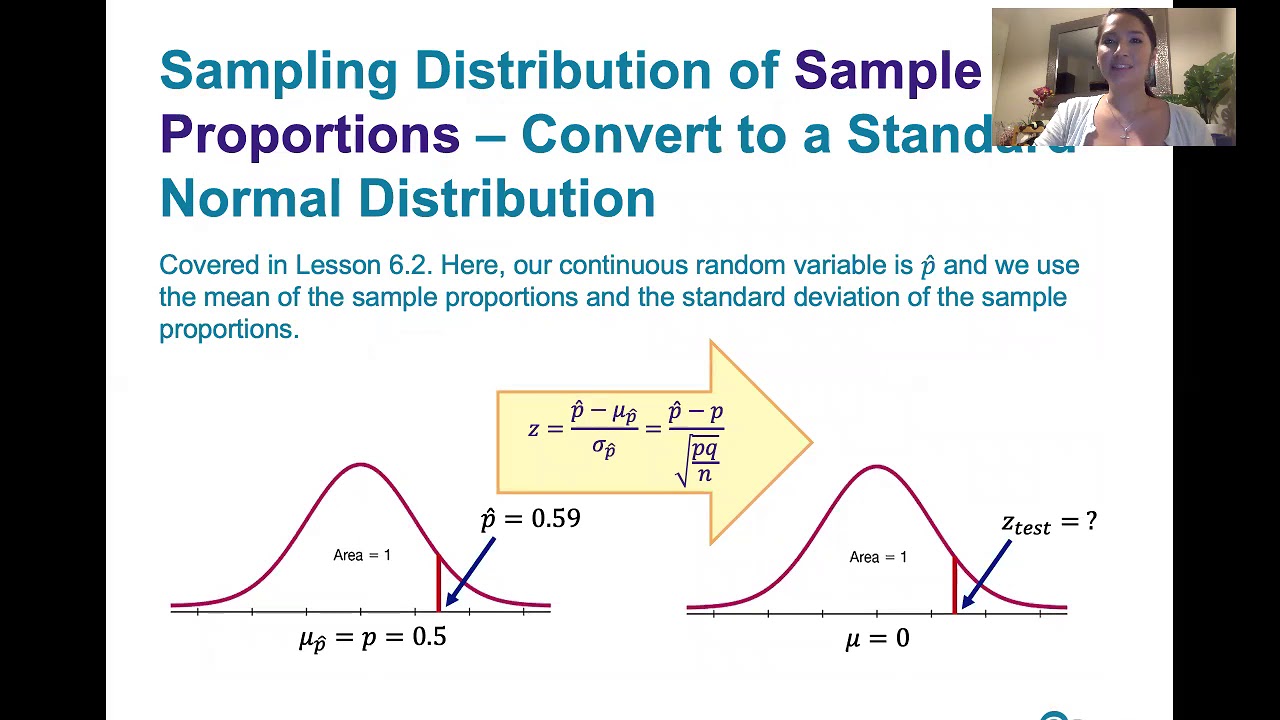
The instructor begins a lesson on hypothesis testing for chapter 8, focusing on sections 8.1 through 8.2, and possibly extending into 8.3. The aim is to complete most of chapter 8 and demonstrate the use of a calculator for hypothesis testing. The specific problem involves a claim about the proportion of religious surfers belonging to a religious community, which is stated to be different from the general population. The claim is that the proportion is 69%, and the task is to test this against a sample of religious surfers to determine if there is a significant difference. The lesson outlines the steps for hypothesis testing, including stating the null hypothesis (p = 0.69) and the alternative hypothesis (p ≠ 0.69), and introduces the concept of a two-tailed test.

05:05

🔢 Calculator Usage for Test Statistic

The instructor proceeds to explain how to use a calculator for finding the test statistic in a hypothesis test. The example involves a two-tailed test with a significance level (alpha) of 0.01. The process includes entering values into the calculator for a '1 prop z test', inputting the null hypothesis proportion (p₀ = 0.69), the sample proportion, and indicating the test is two-tailed. The calculator provides the z-score and the p-value, which is then doubled for a two-tailed test to determine the significance of the result. The instructor corrects a previous mistake regarding the doubling of the p-value and emphasizes the importance of this step in hypothesis testing.

10:09

🚗 Hypothesis Testing for Sports Car Inspections

The script moves on to another hypothesis test scenario involving sports car owners who believe their vehicles are inspected differently at a state vehicle inspection station compared to family-style cars. Historical data suggests that 30% of all passenger cars fail the inspection on the first attempt. The instructor guides through setting up the hypothesis test, with the null hypothesis being that the proportion of first-time failures for sports cars is equal to the general 30%, and the alternative hypothesis being that it is greater than 30%. The test is a right-tailed test, and the significance level is set at 10%. The instructor demonstrates how to use a calculator to find the z-score and the p-value for this test.

15:10

📉 Insufficient Evidence for Sports Car Inspection Bias

After calculating the z-score and p-value using the calculator, the instructor concludes that there is insufficient evidence to support the claim that sports cars are inspected more harshly than other cars. The p-value of 0.186 is greater than the significance level of 0.10, leading to a failure to reject the null hypothesis. This means that based on the sample data, there isn't enough evidence to conclude that the proportion of sports cars failing the inspection is higher than the 30% rate for all passenger cars.

20:16

🎯 Hypothesis Testing for Mean Leisure Time

The instructor introduces a new hypothesis test about the mean amount of leisure time adults in America spend per week, which a past study claimed to be 18 hours. A researcher has taken a sample of 10 adults to test if this leisure time is different. The hypothesis test is set up with the null hypothesis (mu = 18) and the alternative hypothesis (mu ≠ 18), indicating a two-tailed test. The significance level is 10%. The instructor explains the steps for calculating the test statistic using the sample mean, standard deviation, and the t-distribution, which is appropriate for hypothesis tests involving means.

25:19

📊 Calculation of Test Statistic for Leisure Time

The instructor demonstrates how to calculate the test statistic for the leisure time hypothesis test. Using the sample data provided, the mean (x̄) and standard deviation (s) are entered into the calculator to obtain these values. The test statistic is then calculated using the formula for a t-score, which involves the difference between the sample mean and the claimed mean, divided by the standard error (s/√n). The result is a t-score that will be used to determine the p-value and make a decision about the null hypothesis.

30:19

📉 Rejection of Null Hypothesis for Leisure Time

After calculating the test statistic, the instructor proceeds to determine the p-value and make a decision about the null hypothesis. The p-value is found to be 0.024, which is less than the significance level of 0.10. This leads to the rejection of the null hypothesis in favor of the alternative hypothesis that the mean leisure time is different from 18 hours. The instructor emphasizes the importance of understanding the process and being able to justify the statistical decision made.

35:22

🧠 Hypothesis Testing for Maze Solving Time

The instructor presents a psychology experiment scenario involving rats navigating mazes. A researcher wants to find a maze that takes rats an average of 45 seconds to solve. The hypothesis test is set up to determine if the maze takes longer than 45 seconds, with the null hypothesis being that the mean time is equal to 45 seconds and the alternative hypothesis being that it is greater than 45 seconds. The test is a right-tailed test with a significance level of 1%. The instructor explains how to use the calculator to find the test statistic and p-value for this test.

40:26

🔬 Insufficient Evidence for Maze Time Hypothesis

The instructor concludes the psychology experiment scenario by stating that the p-value of 0.0159 is greater than the significance level of 0.01, leading to a failure to reject the null hypothesis. This means there is insufficient evidence to support the claim that the maze takes longer than 45 seconds for rats to solve. The instructor emphasizes the importance of understanding the process of hypothesis testing and being able to interpret the results correctly.

45:29

📏 Hypothesis Testing for Standard Deviation of Pennies

The instructor discusses a scenario where the U.S. Mint requires pennies to have a mean weight of 2.5 grams and a standard deviation of 0.0230 grams. A sample of 30 pennies has a mean weight of 2.4991 grams and a standard deviation of 0.01648 grams. The hypothesis test is set up to determine if the standard deviation is less than what the U.S. Mint specifies, with the null hypothesis being that the standard deviation is equal to 0.0230 grams and the alternative hypothesis being that it is less. The test is a left-tailed test with a significance level of 5%. The instructor explains how to calculate the test statistic using the chi-squared distribution and find the p-value.

50:38

📉 Rejection of Null Hypothesis for Penny Weight Standard Deviation

After calculating the test statistic and the p-value, which is 0.0141, the instructor concludes that the p-value is less than the significance level of 0.05, leading to the rejection of the null hypothesis. This supports the claim that the standard deviation of the weight of pennies is less than what the U.S. Mint specifies. The instructor wraps up by summarizing the steps and processes involved in hypothesis testing for standard deviation and variance, and mentions plans to cover confidence intervals in a future video.

Mindmap

Keywords

💡Hypothesis Testing

Hypothesis testing is a statistical method used to make decisions about the population based on sample data. It is central to the video's theme as the script discusses various steps and examples of hypothesis testing for different statistical measures like proportions, means, and standard deviations. The video script provides a step-by-step guide on how to perform hypothesis testing, including setting up null and alternative hypotheses, determining the test statistic, calculating p-values, and making decisions based on the significance level.

💡Null Hypothesis (H0)

The null hypothesis is a statement of no effect or no difference that is tested using a statistical method. In the context of the video, the null hypothesis is represented with an equal sign (e.g., p = 0.69, mu = 18) and serves as the default assumption that there is no significant difference in the population parameter being tested. The script walks through the process of formulating the null hypothesis as part of the hypothesis testing procedure.

💡Alternative Hypothesis (H1 or Ha)

The alternative hypothesis is a statement that contradicts the null hypothesis, suggesting an effect or difference. It is used to state what we believe to be true if the null hypothesis is rejected. The video script explains that the alternative hypothesis can be less than, greater than, or not equal to the null hypothesis but never includes an equal sign, and it is used to calculate the test statistic and p-value.

💡Significance Level (Alpha)

The significance level, denoted as alpha, is the probability of rejecting the null hypothesis when it is true. It is a threshold used to determine the results of the hypothesis test. The script mentions alpha levels such as 0.01 and 0.10, which represent the risk of incorrectly rejecting the null hypothesis, and it explains how to use these levels to make decisions about the null hypothesis.

💡P-Value

The p-value is the probability of obtaining results as extreme as the observed sample results, assuming the null hypothesis is true. It is a crucial concept in the video, as the script describes how to calculate and interpret p-values in the context of hypothesis testing. The p-value is used to compare with the significance level to decide whether to reject the null hypothesis.

💡Test Statistic

A test statistic is a summary of the data used to test the null hypothesis. The script explains how to calculate different test statistics for various tests, such as z-scores and t-scores, depending on the type of hypothesis test being conducted. The test statistic quantifies the degree to which the sample data deviate from what would be expected if the null hypothesis were true.

💡Type I Error

A Type I error occurs when the null hypothesis is incorrectly rejected. It is the error of 'seeing' an effect when there is none. The script implicitly addresses the concept of Type I error through the significance level, which is the threshold that determines the likelihood of making this error. The lower the alpha level, the lower the chance of committing a Type I error.

💡Type II Error

A Type II error happens when the null hypothesis is failed to be rejected when it is actually false. This is the error of 'missing' an effect that is there. Although the script does not explicitly define Type II error, it discusses the concept of failing to reject the null hypothesis, which can lead to this type of error.

💡Chi-Squared Test

The chi-squared test is a statistical method used to determine if there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. The video script provides an example of using the chi-squared test to test the standard deviation of pennies' weight, illustrating how to calculate the test statistic and p-value for this specific test.

💡T-Test

A t-test is used to determine if there is a significant difference between the means of two groups. The script explains how to perform a t-test for a single sample mean and how to use the calculator to find the test statistic and p-value. The t-test is relevant when the population standard deviation is unknown and the sample size is small.

💡Z-Test

A z-test is a statistical test used to determine if two population proportions are equal. The video script discusses the use of the z-test in the context of hypothesis testing for population proportions, explaining how to calculate the test statistic using the sample proportion and the claimed proportion, and how to interpret the results using the z-score.

💡Population Proportion

Population proportion refers to the ratio of a particular characteristic in the entire population. In the video, the script discusses testing claims about population proportions, such as the proportion of religious surfers or the proportion of sports cars failing an inspection, using hypothesis tests to determine if the sample proportion differs significantly from a claimed value.

💡Sample Mean (x̄)

The sample mean, denoted as x̄, is the average of the values in a sample and is used as an estimate for the population mean. The script frequently refers to the sample mean in the context of hypothesis testing for means, showing how to calculate it and use it in formulas for test statistics and confidence intervals.

💡Sample Size (n)

Sample size is the number of observations or elements in a sample. The script mentions sample size as an important factor in hypothesis testing, as it affects the calculation of the test statistic and the determination of whether the sample is large enough to use certain tests, such as the central limit theorem applications.

💡Standard Deviation (s)

Standard deviation is a measure of the amount of variation or dispersion in a set of values. The script discusses the standard deviation of a sample and how it is used in hypothesis testing, particularly in calculating the test statistic for z-tests and t-tests, and in chi-squared tests for variance.

💡Calculator Functions

The script provides examples of how to use calculator functions to perform hypothesis testing, such as '1 prop z test' for population proportion tests and 't-test' for mean tests. It emphasizes the utility of calculator functions in simplifying the process of hypothesis testing, especially for students taking online exams.

Highlights

Introduction to hypothesis testing for chapter 8, focusing on using a calculator to find test statistics.

Explanation of how to set up null and alternative hypotheses for a claim about a proportion.

Demonstration of using a calculator for a two-tailed test in hypothesis testing.

Clarification on the difference between null and alternative hypotheses and their relationship to equal signs.

Instruction on identifying the type of tail test (left, right, or two-tailed) based on the alternative hypothesis.

Guide on calculating the test statistic using a calculator for a proportion z-test.

Discussion on the importance of doubling the p-value for two-tailed tests when not using a calculator.

Illustration of how to interpret the p-value in relation to the significance level (alpha) to make a statistical decision.

Explanation of failing to reject the null hypothesis and its implications for the evidence in support of a claim.

Transition to hypothesis testing for means, including the formula for the test statistic.

Use of a calculator to find the mean and standard deviation from a given data set.

Calculation of the test statistic for a mean using sample data and the formula.

Comparison of manual calculation with calculator results for verification of test statistic and p-value.

Introduction of hypothesis testing for standard deviation and variance using the chi-squared distribution.

Process of calculating the chi-squared test statistic when the population standard deviation is known.

Use of the chi-squared distribution to find the p-value for a hypothesis test on standard deviation.

Decision-making in hypothesis testing based on the p-value compared to the significance level.

Conclusion on the evidence for the claim about standard deviation being less than specified by the U.S. mint.

Transcripts

Browse More Related Video

Math 119 Chapter 9 part 1

Math 119 Chap 8 part 1

9.2.2 Two Means, Independent Samples - The Rationale Behind The Equivalent Methods, P-value Method

8.1.3 Basics of Hypothesis Testing - Computing and Interpreting Test Statistics

9.2.3 Two Means, Indep. Samples - Critical Value Method, St. Deviations Unknown, Not Assumed Equal

Elementary Statistics Chapter 8 - Introduction Hypothesis Testing Part 1 Lesson 1

Related Tags

Hypothesis Testing Statistical Analysis Calculator Tutorial Educational Content Student Guide Z-Test T-Test Chi-Squared Test Classroom Instruction Statistical Methods Online Learning