Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2

3Blue1Brown
12 Apr 202010:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the concept of probability in the context of a weighted coin with an unknown bias, h. Through an example of flipping the coin ten times and observing seven heads, it delves into the paradox of assigning probabilities to continuous values. The key takeaway is that instead of focusing on individual probabilities, we should consider probability densities, which represent the likelihood of ranges of values. This approach resolves the paradox by using probability density functions (PDFs) and measure theory, which connect finite and continuous probability settings. The video sets the stage for understanding how to derive a PDF from observed data.

Takeaways
  • 🎲 The script discusses a weighted coin with an unknown probability of landing heads, which could vary from 0% to 100%.
  • 🤔 It raises the question of estimating the true probability of heads given observed outcomes, highlighting the complexity of probabilities of probabilities.
  • 📊 The paradox of assigning a probability to continuous values is addressed, where individual probabilities for specific values approach zero but must sum to one.
  • 🛠 The concept of probability density is introduced as a solution to the paradox, where the area under a curve represents the probability of a range of outcomes.
  • 📚 The importance of measure theory is mentioned as a mathematical framework that unifies discrete and continuous probability distributions.
  • 📉 The script explains that in continuous distributions, the probability of a specific value is zero, but the probability across a range is non-zero.
  • 📈 The use of probability density functions (PDFs) is emphasized for understanding the likelihood of a random variable falling within a certain interval.
  • 🔍 The process of refining the understanding of a distribution involves considering finer buckets and approaching a smooth curve as a limit.
  • 📐 The total area under the PDF must equal one, reflecting the total probability of all possible outcomes.
  • 🧩 The script suggests that in practice, using data to estimate the PDF can help answer complex probability questions about the underlying process.
  • 🔑 The takeaway is that understanding the rules of probability in continuous settings is crucial for making meaningful inferences from data.
Q & A

  • What is the main point of the initial discussion about the weighted coin?

    -The main point is to introduce the concept of a weighted coin where the probability of flipping heads is unknown and can vary, highlighting the challenge of determining this probability based on a limited number of flips.

  • Why is it problematic to ask about the probability of the true probability being exactly 0.7?

    -It's problematic because it involves assigning a probability to a specific value within a continuous range, which can lead to paradoxes if not handled correctly.

  • How does the script propose to resolve the paradox of assigning probabilities to continuous values?

    -The script resolves this paradox by focusing on ranges of values rather than individual values and using probability density instead of discrete probabilities.

  • What is the significance of using the area under the curve to represent probability?

    -Using the area under the curve allows for meaningful representation of probabilities in a continuous setting, ensuring that the total probability sums to one and avoids paradoxes associated with individual probabilities.

  • What is a probability density function (PDF), and how is it used?

    -A PDF is a function that describes the probability density of a continuous random variable. The probability of the variable falling within a certain range is given by the area under the curve of the PDF within that range.

  • How does measure theory help in understanding probabilities in continuous settings?

    -Measure theory provides a rigorous mathematical framework for associating probabilities with subsets of possible outcomes, uniting finite and continuous settings and resolving paradoxes associated with continuous probabilities.

  • Why is it necessary to consider ranges of values rather than individual values when dealing with continuous probabilities?

    -Considering ranges of values avoids the problem of assigning non-zero probabilities to an uncountably infinite number of individual values, which would lead to an infinite total probability.

  • What happens to the probabilities of individual values in the continuous setting, according to the script?

    -In the continuous setting, the probability of any single specific value is zero, but the probabilities of ranges of values remain meaningful.

  • How do integrals relate to probabilities in continuous settings?

    -In continuous settings, integrals are used to calculate the area under the curve of a probability density function, representing the probability of a random variable falling within a specific range.

  • What practical question does the script aim to address regarding the weighted coin?

    -The script aims to address the practical question of how to use data to create meaningful answers to probabilities of probabilities questions, such as finding the probability density function for the true probability of flipping heads.

Outlines
00:00
🎲 Understanding Probabilities with a Biased Coin

This paragraph introduces a thought experiment involving a weighted coin with an unknown probability of landing heads. It discusses the difficulty of assigning a probability to the true probability of heads (denoted as 'h') and the paradox that arises when considering the infinitesimally small probabilities of each possible value of 'h'. The solution proposed is to consider ranges of values for 'h' rather than individual values, emphasizing the importance of using areas to represent probabilities in continuous distributions, which helps to resolve the paradox.

05:02
📊 The Concept of Probability Density Function (PDF)

The second paragraph delves into the concept of a Probability Density Function (PDF), explaining how it allows for the assignment of a meaningful probability to ranges of continuous values, thus avoiding the paradoxes associated with discrete probabilities. It clarifies that the probability of a specific value is zero in a continuous distribution, but the area under the PDF curve between two values represents the probability of the random variable falling within that range. The paragraph also touches on the shift in rules for combining probabilities in continuous versus discrete settings and briefly introduces measure theory as a mathematical framework that unifies these concepts.

Mindmap
Keywords
💡Weighted Coin
A 'weighted coin' refers to a coin that does not have a 50-50 chance of landing on heads or tails due to an uneven distribution of weight. In the video, it is used to illustrate a scenario where the probability of getting heads is unknown and could vary significantly. The concept is central to discussing the nature of probability in continuous settings, as it sets the stage for exploring the paradox of assigning probabilities to unknown, continuous variables.
💡Probability
Probability is a measure of the likelihood that a particular event will occur, expressed as a number between 0 and 1. In the context of the video, it is used to discuss the challenges of determining the likelihood of outcomes when dealing with a weighted coin, where the true probability of heads is unknown. The script explores the concept of probability in both discrete and continuous scenarios, highlighting the complexities involved in assigning probabilities to events with an infinite number of possible outcomes.
💡Continuous Values
Continuous values refer to a range of numbers that can take on any value within a given interval, as opposed to discrete values which are separated by distinct gaps. The video uses the concept of continuous values to discuss the paradox of assigning probabilities to every possible outcome of a random event, such as the probability of flipping heads on a weighted coin, where the probability 'h' could be any real number between 0 and 1.
💡Paradox
A paradox is a statement or situation that seems self-contradictory or logically unacceptable. In the script, the paradox arises when considering the probability of a specific value for 'h', the probability of flipping heads. The video points out that if every specific value has a non-zero probability, the total probability would be infinite, which is a logical contradiction, thus creating a paradox.
💡Probability Density
Probability density is a concept used in continuous probability distributions, where instead of having a probability for each individual outcome, we have a density function that describes the likelihood of outcomes within a range. The video explains that the height of the bars in a histogram (representing ranges of 'h') represents the probability density, which is crucial for understanding how to calculate probabilities over continuous ranges without running into paradoxes.
💡Probability Density Function (PDF)
A Probability Density Function (PDF) is a function that describes the likelihood of a continuous random variable taking on a particular value. The video introduces the PDF as a tool to resolve the paradox of assigning probabilities to continuous values. The area under the PDF curve between two values gives the probability of the random variable falling within that range, which is a key concept in understanding continuous probability distributions.
💡Measure Theory
Measure theory is a branch of mathematical analysis that studies sets, particularly infinite ones, and assigns a 'size' or 'measure' to them. In the video, measure theory is mentioned as a field that helps to formalize and unify the concept of assigning probabilities to various subsets of possibilities, including those in continuous settings. It provides a rigorous foundation for the rules governing how probabilities are combined and distributed.
💡Integral
An integral is a mathematical concept used to calculate the area under a curve, which is a fundamental tool in calculus. In the context of the video, integrals are used to find the area under the PDF curve, representing the probability of a random variable falling within a certain range. The video suggests that integrals are the continuous counterpart to sums in discrete contexts, providing a way to work with probabilities over continuous ranges.
💡Random Variable
A random variable is a variable whose possible values are determined by chance, often associated with the outcomes of a random event. In the video, the random variable is the unknown probability 'h' of flipping heads on the weighted coin. The concept of random variables is central to understanding how probabilities are assigned and calculated in both discrete and continuous settings.
💡Dartboard
The dartboard analogy is used in the video to illustrate the concept of a continuous probability distribution, where outcomes are real numbers that can be thought of as points on a dartboard. The video uses this analogy to help explain the idea that in continuous distributions, individual outcomes can have a probability of zero, yet collectively they sum to one, which is a key insight in understanding continuous probability.
Highlights

Introduction of a hypothetical weighted coin with an unknown probability of landing heads.

Discussion of the paradoxical nature of assigning probabilities to continuous values.

The concept of a probability density function (PDF) as a solution to the paradox of continuous probabilities.

Explanation of how the area under a PDF curve represents the probability of a range of outcomes.

The importance of considering ranges of values rather than individual values in continuous probability.

The idea that as the width of probability buckets decreases, the height remains constant, leading to a smooth curve.

Clarification that the height of the PDF represents the probability density, not the probability itself.

The necessity for the total area under the PDF to equal one, reflecting a valid probability distribution.

The distinction between discrete and continuous probability settings and how they are handled differently.

Introduction to measure theory as a mathematical framework that unifies discrete and continuous probability.

The practical application of using data to estimate the probability density function of an unknown parameter.

The transition from discrete sums to continuous integrals as a common rule of thumb in probability.

The deeper theoretical underpinnings of integrals in relation to measure theory and probability.

The intuitive challenge of understanding how individual outcomes with zero probability can sum to one in continuous settings.

The realization that the rules for combining probabilities change between finite and continuous settings.

The practical question of estimating the true probability of flipping heads given observed outcomes.

The teaser for the next part of the video where the PDF will be derived from observed data.

Transcripts

Browse More Related Video

6.1.1 The Standard Normal Distribution - Discrete and Continuous Probability Distributions

Probability density functions | Probability and Statistics | Khan Academy

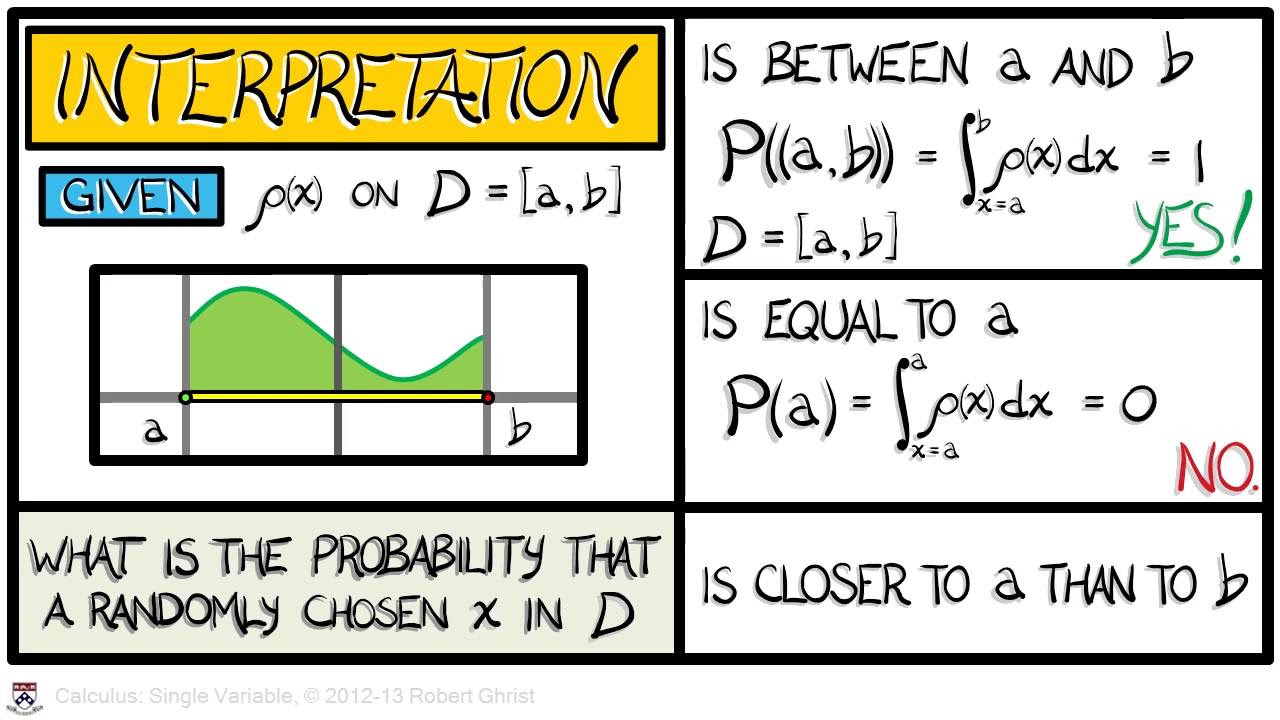
Calculus Chapter 4 Lecture 43 Probability Densities

Constructing a probability distribution for random variable | Khan Academy

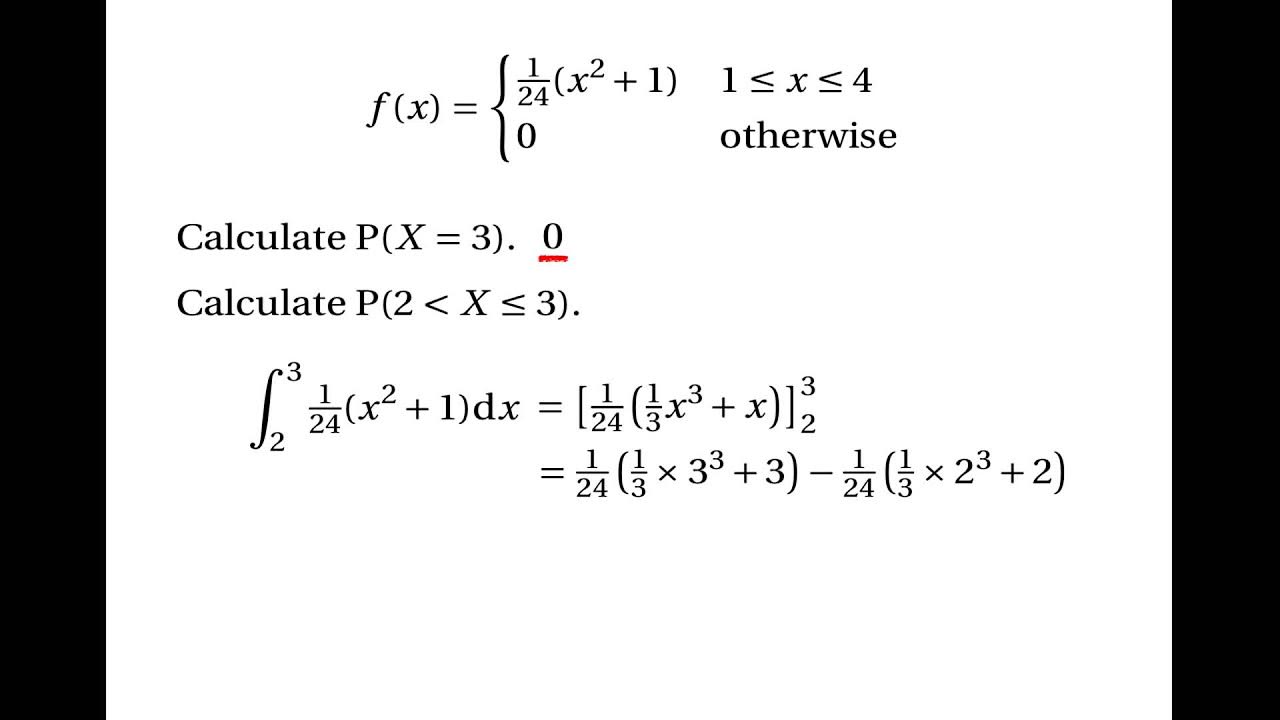
Continuous Random Variables: Probability Density Functions

6.1.2 The Standard Normal Distribution - Uniform Distributions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Probability TheoryWeighted CoinContinuous ValuesMeasure TheoryParadox ResolutionRandom EventsProbability DensityIntegral CalculusData AnalysisStatistical Learning