5.1.1 Discrete Probability Distributions - Discrete and Continuous Random Variables
TLDRThis video script explores the concept of random variables, distinguishing between discrete and continuous types. It explains that random variables are numerical and determined by chance, with examples like rolling a die for discrete values. Discrete variables have countable outcomes, such as coin tosses until heads appears, while continuous variables, like body temperatures, have an uncountable range of values. The script also provides criteria to determine if a quantity is a random variable and its type, using examples like baby weights and shoe sizes.
Takeaways
- 🎲 A random variable, typically denoted by 'x', is a numerical value determined by chance for each outcome of a procedure.
- 📊 Random variables represent quantitative data and are categorized into discrete and continuous types.
- 🔢 Discrete random variables have a finite or countably infinite set of values, such as the number of coin tosses until the first heads appears.
- 📏 Discrete variables can be visualized on a number line with distinct points, like counting the number of movie patrons entering a theater.
- ∞ Continuous random variables have an uncountably infinite number of values, such as body temperatures which exist over a range.
- 📉 Continuous variables can be represented on a number line as an interval, reflecting the impossibility of counting the infinite values within.
- 🔋 An example of a continuous random variable is the measured voltage on a battery, which exists over a range of values.
- 👶 The exact weights of the next 100 babies born in the U.S. are a continuous random variable due to the range of possible weights.
- 📊 Responses to a survey question about political party preference are neither discrete nor continuous as they are not numerical data.
- 🎰 The number of spins on a roulette wheel to get a certain number is a discrete random variable because it involves counting.
- 👣 Exact foot lengths of humans are a continuous random variable as they vary over a range of values.
- 👟 Shoe sizes, with specific increments like whole numbers or half sizes, are discrete random variables because they do not have infinitely many values between sizes.
Q & A
What is a random variable?
-A random variable is a variable, typically represented by x, that has a single numerical value determined by chance for each outcome of a procedure.
What are the two main types of random variables?
-The two main types of random variables are discrete random variables and continuous random variables.
What is a discrete random variable?
-A discrete random variable is a random variable that can take on a finite or countably infinite number of values, such as the number of coin tosses before getting heads.
How can you visualize a discrete random variable?
-A discrete random variable can be visualized on a number line with distinct points graphed on it, representing each possible value.
What is a continuous random variable?
-A continuous random variable is a random variable that can take on an infinite number of values within a range, such as body temperatures.
How is a continuous random variable represented on a number line?
-A continuous random variable is represented on a number line as an interval, showing the range of possible values rather than discrete points.
Why can't continuous random variables be counted?
-Continuous random variables cannot be counted because there are infinitely many values within any given interval, making it impossible to list or count them all.
What is an example of a discrete random variable from the script?
-An example of a discrete random variable from the script is the number of movie patrons at a movie theater, which can be counted as they enter.
What is an example of a continuous random variable from the script?
-An example of a continuous random variable from the script is the measured voltage on a battery, which can vary over a range of values.
How can you determine if a quantity is a discrete or continuous random variable?
-You can determine if a quantity is a discrete or continuous random variable by checking if it has a finite or countably infinite set of values (discrete) or an infinite range of values (continuous).
Why is the response to a survey question about political party preference neither a discrete nor a continuous random variable?
-The response to a survey question about political party preference is neither a discrete nor a continuous random variable because it is not numerical data; it is categorical.
Outlines
🎲 Understanding Random Variables
This paragraph introduces the concept of random variables, which are numerical values determined by chance for each outcome of a procedure. It explains that random variables can be either discrete, with a finite or countably infinite set of values, or continuous, with an uncountably infinite range of values. Examples such as rolling a die and counting coin tosses illustrate discrete variables, while body temperatures and measured voltages represent continuous variables. The paragraph also discusses how to visually represent these variables on a number line, with discrete variables having distinct points and continuous variables covering intervals.
📏 Classifying Random Variables: Discrete vs. Continuous
The second paragraph delves into classifying random variables by providing examples and distinguishing between discrete and continuous types. It uses the exact weights of the next 100 babies born as an example of a continuous random variable due to the range of possible weights. Responses to a survey question about political party preference are highlighted as neither discrete nor continuous because they are not numerical. The number of spins on a roulette wheel and human foot lengths are identified as continuous variables due to their range of values, while shoe sizes are discrete because they are countable and do not have infinitely many values between sizes. The paragraph concludes with a summary of the criteria for classifying variables and examples to reinforce the concepts discussed.
Mindmap
Keywords
💡Random Variable
💡Discrete Random Variable
💡Continuous Random Variable
💡Sample Space
💡Quantitative Data
💡Countable Infinity
💡Number Line
💡Interval
💡Voltage
💡Shoe Size
💡Survey Responses
Highlights
A random variable is defined as a variable that has a single numerical value determined by chance for each outcome of a procedure.
Random variables represent quantitative data and can be categorized into discrete or continuous types.
Discrete random variables have a countable set of values, either finite or infinite.
Examples of discrete random variables include the number of coin tosses until getting heads and the count of movie patrons.
Continuous random variables have an uncountable infinite number of values, such as body temperatures.
Continuous random variables can be represented on a number line with an interval, unlike discrete variables which are represented by distinct points.
An example of a continuous random variable is the measured voltage on a battery.
A quantity is considered a random variable if it is numerical and determined by chance.
The exact weights of the next 100 babies born in the United States are an example of a continuous random variable.
Responses to a survey question about political party preference are neither discrete nor continuous random variables as they are not numerical data.
The number of spins on a roulette wheel to get a certain number is a discrete random variable because it involves counting.
Exact foot lengths of humans are continuous random variables as they vary over a range.
Shoe sizes are discrete random variables because they have specific values without infinite subdivisions between them.
The video provides a clear distinction between discrete and continuous random variables with practical examples.
Understanding the difference between discrete and continuous random variables is crucial for statistical analysis and probability theory.
The video explains how to determine whether a quantity is a discrete, continuous, or neither type of random variable.
The concept of random variables is fundamental in various fields such as statistics, economics, and engineering.
Transcripts
Browse More Related Video

Introduction to Discrete Random Variables and Discrete Probability Distributions

Discrete and continuous random variables | Probability and Statistics | Khan Academy

6.1.1 The Standard Normal Distribution - Discrete and Continuous Probability Distributions

Random Variables and Probability Distributions
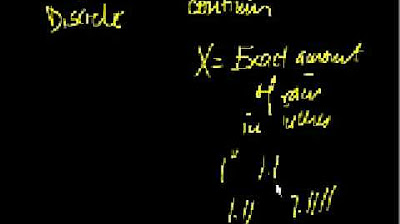
Introduction to Random Variables
Probability density functions | Probability and Statistics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: