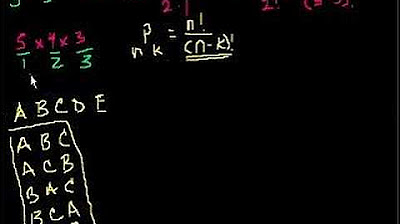Permutations
TLDRThis educational script explores the concept of permutations, illustrating how to calculate the number of ways objects can be arranged in a specific order. It begins with a simple example of 7 people sitting in 3 chairs, explaining the process of multiplying possibilities for each chair. The script then moves to a smaller example with 3 balls and 2 cups, demonstrating different arrangements. It concludes with a general formula for calculating permutations, nPr or P(n, r), which is n! divided by (n-r)!, providing a clear understanding of how to determine the number of possible arrangements when the order matters.
Takeaways
- 😀 The script discusses permutations, which are the different ways items can be arranged in a specific order.
- 🔑 It uses the example of 7 people trying to sit in 3 chairs to illustrate the concept of permutations.
- 👥 The first chair has 7 options, the second chair has 6 remaining options, and the third chair has 5 remaining options after the first two are filled.
- 🧠 To calculate the total number of permutations, multiply the number of options for each chair (7 * 6 * 5 = 210).
- 📚 The script provides a smaller example with 3 balls and 2 cups to further explain permutations.
- 🎯 In the balls and cups example, there are 3 options for the first cup and 2 remaining options for the second cup, leading to 3 * 2 = 6 permutations.
- 📝 The general formula for permutations is nPr = n! / (n - r)!, where n is the total number of items and r is the number of spaces.
- 📈 The formula is derived from the idea of multiplying the number of options for each space until no more spaces are left.
- 💡 The script emphasizes that permutations are about the order of arrangement, unlike combinations where order does not matter.
- 📌 The script also explains that the formula nPr can be visualized as taking the first r components of n factorial.
- 🔍 The video is educational and aims to clarify the concept of permutations with examples and a step-by-step explanation of the formula.
Q & A
What is the problem presented in the transcript?
-The problem is determining the number of different ways 7 people can sit in 3 chairs.
How many possibilities are there for the first person to sit in the first chair?
-There are 7 possibilities for the first person to sit in the first chair since any of the 7 people can sit there.
After one person sits in the first chair, how many people are left to sit in the second chair?
-After one person sits in the first chair, there are 6 people left to sit in the second chair.
What is the total number of possibilities for the first three chairs if no one has sat down yet?
-The total number of possibilities is 7 (for the first chair) times 6 (for the second chair) times 5 (for the third chair), which equals 210.
What is an example given to illustrate a smaller problem?
-A smaller example given is determining the number of different ways 3 balls can be put into 2 cups.
How many possibilities are there for placing 3 balls into 2 cups?
-There are 3 possibilities for the first cup and then 2 possibilities for the second cup after one ball is placed, resulting in 3 times 2, which equals 6 possibilities.
What is the general formula for calculating permutations of n things into k spaces?
-The general formula for calculating permutations is n factorial (n!) divided by (n - k) factorial ((n - k)!).
Why do we multiply the possibilities for each spot when calculating permutations?
-We multiply the possibilities for each spot because for each distinct choice made for one spot, the number of choices for the next spot decreases, and we consider all possible orderings.
How does the script explain the concept of permutations?
-The script explains permutations through examples of people sitting in chairs and balls being placed in cups, emphasizing that the order of placement matters.
What is the difference between permutations and combinations as implied by the script?
-Permutations involve arranging items in a specific order, which matters, while combinations imply that the order does not matter. The script focuses on permutations but mentions that combinations will be discussed in a future video.
How does the script help the viewer understand the concept of factorials in the context of permutations?
-The script relates factorials to the process of filling spots, where n factorial represents all possible ways to fill n spots, and (n - k) factorial represents the ways to fill after k spots are already filled.
Outlines
🪑 Permutations of People and Chairs
The script begins with a scenario involving 3 chairs labeled 1, 2, and 3, and 7 people labeled A through G. The main question posed is how many different ways these 7 people can be seated in the 3 chairs. The explanation proceeds by considering the choices available for each chair, starting with 7 options for the first chair, then 6 for the second, and 5 for the last, leading to a total of 7 x 6 x 5 = 210 possible seating arrangements. This approach is then illustrated with a smaller example involving 3 balls and 2 cups, resulting in 3 x 2 = 6 different ways to distribute the balls. The concept of permutations is introduced as the ordering of items matters, and the notation for permutations is explained, showing how the number of permutations can be calculated.
📚 General Formula for Permutations (nPr and nPk)
The second paragraph delves into finding a general formula for permutations, denoted as nPr or nPk, which represents the number of ways to arrange n distinct items into r (or k) spots. Using an analogy with spots and possibilities, the script explains that for the first spot there are n options, then n-1 for the second, and so on, down to n-k+1 for the kth spot. The pattern is established that for each spot, the number of possibilities is n minus the spot's position number. The script then relates this to the concept of factorial, where nPr is the product of the first r numbers in n factorial, and kPr is the product of the first k numbers in k factorial. The formula for permutations is simplified to n! / (n-k)!, which is demonstrated with examples to show its validity and ease of calculation. The explanation emphasizes understanding the process rather than just memorizing the formula.
👋 Conclusion and Transition to Combinations
In the final paragraph, the script wraps up the discussion on permutations and reassures the viewer that the explanation provided should clarify any confusion. It then teases the next topic to be covered in the series, which is combinations. This sets the stage for further exploration of combinatorial mathematics, suggesting a continuation of the educational journey beyond the current topic.
Mindmap
Keywords
💡Permutations
💡Factorial
💡Chairs and People
💡Cups and Balls
💡Possibilities
💡Labeling
💡Multiplication Principle
💡nPr Notation
💡General Formula
💡Ordering
💡Combination vs. Permutation
Highlights
Exploring the number of ways 7 people can sit in 3 chairs, highlighting the concept of permutations.
Starting with chair one, there are 7 possibilities for the first person to sit.
After one person sits, 6 people remain for chair two.
With two people seated, 5 possibilities for the third chair.
Multiplying possibilities for each chair to find total arrangements.
Calculating the total number of possibilities as 7 x 6 x 5 = 210.
Demonstrating a smaller example with cups and balls to illustrate the concept.
Using 3 balls and 2 cups to show different ways to distribute items.
Calculating 3 balls in 2 cups as 3 x 2 = 6 possibilities.
Discussing the importance of order in permutations.
Providing a visual representation of the 6 ways to distribute 3 balls into 2 cups.
Introducing permutation notation and its mathematical representation.
Explaining the general formula for permutations as nPr = n! / (n-k)!.
Deriving the formula by analogy with spots and possibilities.
Visualizing the factorial process and how it relates to permutations.
Clarifying the permutation formula with examples and cancellation of terms.
Reiterating the permutation concept and its practical applications.
Teasing the next video on combinations to further explore combinatorial mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: