4.4.3 Counting - Permutations and Combinations, and the Permutation Rule

Sasha Townsend - Tulsa
11 Oct 202009:36
EducationalLearning
32 Likes 10 Comments

TLDRThis video covers learning outcome number three for lesson 4.4, focusing on the distinction between permutations and combinations. It explains that permutations involve order, while combinations do not. Using intuitive and formula-based approaches, the video demonstrates how to calculate permutations, illustrated by examples such as medal placements in the Olympics and horse race trifecta bets. The video also discusses the probability of selecting the correct order in such bets, emphasizing the importance of understanding permutations in various contexts.

Takeaways
  • 😀 The video discusses the difference between permutations and combinations, emphasizing that order matters in permutations but not in combinations.
  • 🔍 Permutations involve arranging items where different sequences are counted separately, while combinations consider different sequences as the same.
  • 📚 A mnemonic for remembering permutations and combinations is 'position' for permutations, as positions make a difference, and 'committee' for combinations, where rearrangements do not matter.
  • 🏅 An example of permutations is medalists at the Olympics, where the order of gold, silver, and bronze matters.
  • 🏢 An example of combinations is forming a committee, where the order of members does not affect the composition of the committee.
  • 📈 The permutation rule for counting is given by \( \frac{n!}{(n-r)!} \), where \( n \) is the total number of items and \( r \) is the number of items selected without replacement.
  • 🏇 The video uses a trifecta bet in a horse race as an example to illustrate the permutation formula, where the correct selection of horses in the first, second, and third place is required.
  • 🔢 In the example, with 19 horses in the Kentucky Derby, there are 5,814 different possible trifecta bets, calculated by multiplying the choices for each place (19 * 18 * 17).
  • 🎯 The formula for permutations simplifies to the intuitive approach when the factorial terms cancel out, leaving the product of the choices for each place.
  • 🤔 The probability of winning a specific trifecta bet is the number of ways to select the horses in that exact order divided by the total number of possible arrangements.
  • ⚠️ Not all possible trifecta bets have the same chance of winning due to differences in the horses' abilities, so the calculated probability is based on the assumption of equal chances.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is understanding the difference between permutations and combinations, and learning the permutation rule for counting permutations.

  • What is the key difference between permutations and combinations?

    -The key difference is that in permutations, the order of items matters, while in combinations, the order does not matter.

  • What is a mnemonic for remembering the difference between permutations and combinations?

    -The mnemonic is 'permutations, position' because with permutations, the position of items makes a difference.

  • Can you provide an example of a situation where permutations are relevant?

    -An example is the medalists at the Olympics, where the order of gold, silver, and bronze matters.

  • How about a situation where combinations are relevant?

    -A situation with combinations could be forming a committee, where the order of members does not matter.

  • What is the formula for calculating the number of permutations when selecting r items from n available items without replacement?

    -The formula is n! / (n - r)!, where n! represents the factorial of n.

  • In the context of the video script, what is a trifecta bet in a horse race?

    -A trifecta bet is won by correctly selecting the horses that finish first, second, and third in the correct order.

  • How many different trifecta bets are possible in a race with 19 horses?

    -There are 5,814 different trifecta bets possible, calculated using the permutation formula or the intuitive approach.

  • What is the probability of winning a trifecta bet if a better selects three specific horses in a particular order?

    -The probability is 1/5,814, assuming all possible trifecta bets have the same chance of winning.

  • Do all different possible trifecta bets have the same chance of winning?

    -No, they do not. The assumption of equal chances is for the sake of calculation, but in reality, some horses are faster and have different probabilities of winning.

  • Why might the calculated probability of winning a trifecta bet not be accurate?

    -The calculated probability might not be accurate because it does not account for the varying speeds and track records of the horses, which affect their actual chances of winning.

Outlines
00:00
📚 Understanding Permutations and Combinations

This paragraph introduces learning outcome number three for lesson 4.4, focusing on the distinction between permutations and combinations. It explains that permutations involve ordered arrangements where different sequences are counted separately, using the example of arranging the letters 'a', 'b', and 'c'. In contrast, combinations are unordered arrangements where the sequence does not affect the count, illustrated by considering the same letters as part of a combination regardless of order. The mnemonic 'permutations, position' is introduced to emphasize the importance of order in permutations, with examples like Olympic medalists for permutations and committee members for combinations. The permutation rule for counting is also introduced, explaining the formula for calculating the number of permutations when selecting 'r' items from 'n' available items without replacement.

05:02
🏇 Applying Permutations in a Trifecta Bet Scenario

The second paragraph delves into applying the permutation concept to a trifecta bet in a horse race, where the order of the horses finishing first, second, and third matters. It uses the example of the 140th running of the Kentucky Derby with 19 horses to calculate the total number of possible trifecta bets. The intuitive approach to calculating permutations is explained, multiplying the number of choices for each place (19 for first, 18 for second, and 17 for third) to arrive at 5,814 possible bets. The paragraph also revisits the permutation formula, demonstrating how it simplifies to the same result as the intuitive approach. The discussion then moves to part B of the question, which involves calculating the probability of a specific trifecta bet winning and addresses the assumption that all bets have the same chance of winning, concluding that this may not be accurate due to varying horse speeds and track records.

Mindmap
Keywords
💡Permutations
Permutations refer to the arrangement of items where the order is significant. In the context of the video, permutations are used to explain the concept of different sequences of the same set of items being counted as separate entities. For example, with the letters 'a', 'b', and 'c', all possible sequences (abc, acb, bca, etc.) are considered unique permutations. This concept is crucial for understanding scenarios like the Olympic medalists where the order of receiving gold, silver, and bronze matters.
💡Combinations
Combinations are arrangements of items where the order does not affect the count, and different sequences of the same items are considered the same. The video uses the analogy of forming a committee, where the order of selection does not matter, to illustrate combinations. All that matters is the composition of the committee, not the sequence in which members were chosen, making it a combination rather than a permutation.
💡Order
The term 'order' in the video signifies the sequence or arrangement of items. It is a fundamental differentiator between permutations and combinations. The video emphasizes that in permutations, the order is essential, as seen in the example of medal placements at the Olympics. In contrast, for combinations, such as forming a committee, the order is irrelevant.
💡Mnemonic
A mnemonic is a memory aid used to help remember complex information. The video introduces the mnemonic 'position' for permutations to emphasize that the position of items in a sequence is crucial. This aids in distinguishing between permutations, where position matters, and combinations, where it does not.
💡Factorial
Factorial, denoted by 'n!', is the product of all positive integers up to 'n'. The video explains the use of factorial in calculating permutations, where 'n!' represents the total number of ways to arrange 'n' items. It is integral to the permutation formula, which is used to find the number of possible arrangements when order matters.
💡Permutation Rule
The permutation rule is a formula used to calculate the number of permutations when 'r' items are selected from 'n' available items without replacement. The video presents the formula as n! / (n - r)!, which is derived from the multiplication counting rule and factorial counting rule. It is exemplified by calculating the number of possible trifecta bets in a horse race.
💡Tricecta Bet
A trifecta bet, as mentioned in the video, is a type of wager in horse racing where a bettor must select the horses that will finish first, second, and third in the correct order. The video uses this as an example to illustrate the application of the permutation rule, emphasizing that the order of selection is crucial for winning such a bet.
💡Probability
Probability in the video refers to the likelihood of a particular outcome occurring, such as the chance of winning a trifecta bet by randomly selecting horses in a specific order. The video calculates this probability by dividing the number of ways a specific selection can occur by the total number of possible arrangements, highlighting the difference between theoretical probability and actual likelihood based on each horse's performance.
💡Intuitive Approach
The intuitive approach is a method of understanding and solving problems by using common sense and basic reasoning. The video encourages learning this approach for calculating permutations, as opposed to just memorizing the formula, to gain a deeper understanding of why a certain number of permutations exist.
💡Formula
In the context of the video, a formula is a mathematical expression used to calculate specific values, such as the number of permutations. The video discusses the permutation formula and its application in the trifecta bet example, while also emphasizing the importance of understanding the intuitive approach to avoid blind formula application.
Highlights

The video discusses the difference between permutations and combinations, focusing on whether order matters in arrangements.

Permutations involve different sequences of the same items counted separately, while combinations do not consider order.

A mnemonic for remembering permutations and combinations is 'position' for permutations and 'committee' for combinations.

An example of permutations is medalists at the Olympics, where the order of receiving gold, silver, and bronze matters.

An example of combinations is forming a committee, where the order of selection does not affect the final group.

The permutation rule for counting is introduced, using the formula n! / (n-r)! for n different items and r selections without replacement.

The formula for permutations is derived from the multiplication counting rule and factorial counting rule.

An intuitive approach to calculating permutations is demonstrated using the example of a trifecta bet in a horse race.

The 140th running of the Kentucky Derby had 19 horses, and the number of possible trifecta bets is calculated.

The intuitive approach results in 5,814 possible trifecta bets, which matches the result from the permutation formula.

The video emphasizes the importance of understanding the intuitive approach to permutation calculations rather than just applying a formula.

Part B of the question explores the probability of winning a trifecta bet by selecting specific horses in a specific order.

The probability calculation assumes all possible trifecta bets have the same chance of winning, which may not be accurate in reality.

The video concludes by noting that the calculated probability may not reflect the true chances of winning due to varying horse speeds and track records.

The video encourages learning the intuitive approach for a deeper understanding of permutations and their applications.

Transcripts

Browse More Related Video

01 - What is a Permutation? Learn the Permutation Formula.

4.4.5 Counting - Permutations and Combinations and the Combinations Rule

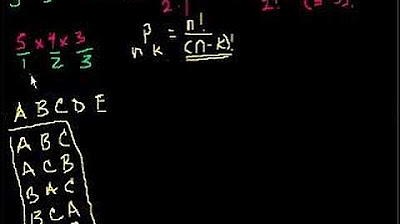
Combinations

4.4.0 Counting - Lesson Overview, Learning Outcomes, and Key Concepts

Statistics Lecture 4.7: Fundamental Counting Rule, Permutations and Combinations

4.4.2 Counting - The Factorial Rule

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PermutationsCombinationsMathematicsEducationalLearningOrder MatterSequencesCounting RuleProbabilityOlympicsKentucky Derby