Carnot Heat Engines, Efficiency, Refrigerators, Pumps, Entropy, Thermodynamics - Second Law, Physics
TLDRThis educational video script delves into the second law of thermodynamics, focusing on heat engines, efficiency, and refrigerators. It explains the concept of reversible and irreversible processes, the natural flow of heat, and the entropy increase in disorderly systems. The script covers the working principles of heat engines and refrigerators, introduces the Carnot cycle as an ideal model for maximum efficiency, and discusses the coefficient of performance for heat pumps and refrigerators. It also touches on the Otto cycle used in gasoline engines and concludes with entropy calculations for various scenarios, emphasizing the zero net change in entropy for cyclic reversible processes.
Takeaways
- ๐ The first law of thermodynamics is essentially a statement of energy conservation, where the change in internal energy equals heat added minus work done by the system.
- ๐ The second law of thermodynamics highlights that irreversible processes increase the disorder of a system, with heat naturally flowing from hot to cold and not the reverse, unless external energy is applied.
- ๐ง Reversible and irreversible processes are differentiated by whether they can occur spontaneously and without external influence; reversible processes can occur in either direction without friction.
- ๐ก๏ธ Heat engines are devices that convert heat energy into mechanical work, with efficiency being the ratio of work done to heat absorbed, highlighting that not all absorbed heat is converted to work.
- โ๏ธ In heat engines, the work performed is calculated as the difference between the heat absorbed (qh) and the heat expelled (qc), and efficiency is the ratio of work to absorbed heat, expressed as a percentage.
- โ๏ธ Jet engines and other heat engines operate on the principle of absorbing heat and performing work, with the specific amounts of heat and work determining the engine's efficiency and power output.
- ๐ Auto cycles, like those in gasoline engines, involve adiabatic compression followed by isochoric heating, adiabatic expansion, and isochoric cooling, with efficiency determined by the compression ratio and gamma ratio.
- ๐ The Carnot engine is an ideal model representing the maximum possible efficiency of a heat engine, with its efficiency calculated based on the temperatures of the hot and cold reservoirs.
- ๐ Refrigerators and air conditioners work opposite to heat engines, using work input to transfer heat from a cold to a hot reservoir, with the coefficient of performance่กก้ing efficiency in this direction.
- โ๏ธ The Carnot refrigerator has a maximum coefficient of performance calculated based on the temperatures of the reservoirs, with actual refrigerators having a lower performance coefficient.
- ๐ Entropy is a measure of disorder, increasing with the expansion of gases and rise in temperature, with the change in entropy calculated for isothermal processes using the heat transferred divided by temperature.
Q & A
What is the first law of thermodynamics?
-The first law of thermodynamics is a statement of the conservation of energy, which states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system, expressed as ฮU = Q - W.
Can you explain the concept of reversible and irreversible processes in thermodynamics?
-Reversible processes are those that can occur in either direction without any external influence, like a ball rolling on a level surface in either direction. Irreversible processes, on the other hand, occur naturally in only one direction and require external energy to reverse, such as a ball falling to the ground but not rising on its own.
What does the second law of thermodynamics state about the flow of heat?
-The second law of thermodynamics states that heat always flows from a region of higher temperature to a region of lower temperature and never in the reverse direction without external work being done.
What is the difference between a heat engine and a refrigerator in terms of energy conversion?
-A heat engine converts heat energy into mechanical work by absorbing heat from a high-temperature reservoir and expelling some of it to a low-temperature reservoir. A refrigerator, conversely, uses electrical energy to pump heat from a low-temperature reservoir to a high-temperature reservoir.
How is the efficiency of a heat engine calculated?
-The efficiency of a heat engine is calculated as the ratio of the work done by the engine to the heat energy absorbed from the high-temperature reservoir, expressed as a percentage. Mathematically, it is given by (W/Qh) ร 100%.
What is the significance of the Carnot cycle in the context of heat engines?
-The Carnot cycle represents the ideal model of a heat engine, which achieves the maximum possible efficiency between two given temperatures. No real engine can be more efficient than a Carnot engine operating between the same temperature limits.
What is the formula for calculating the efficiency of a Carnot engine?
-The efficiency of a Carnot engine is given by the formula ฮท = 1 - (Tc/Th), where Tc is the temperature of the cold reservoir and Th is the temperature of the hot reservoir, both in Kelvin.
How is the coefficient of performance (COP) for a refrigerator defined?
-The coefficient of performance for a refrigerator is defined as the ratio of the heat removed from the cold reservoir (Qc) to the work input (W) required to run the refrigerator, expressed as COP = Qc/W.
What is the concept of entropy in thermodynamics and how is it related to the second law?
-Entropy is a measure of the disorder or randomness in a system. The second law of thermodynamics states that for irreversible processes, the total entropy of a system tends to increase, indicating a natural progression towards a more disordered state.
How is the change in entropy calculated for an isothermal process?
-For an isothermal process, the change in entropy (ฮS) can be calculated using the formula ฮS = Q/T, where Q is the heat transferred and T is the absolute temperature at which the process occurs.
What is the Otto cycle and how does it relate to the efficiency of a gasoline engine?
-The Otto cycle is an idealized model of a gasoline engine, involving adiabatic compression, isochoric heating, adiabatic expansion, and isochoric cooling. The efficiency of an Otto cycle is given by ฮท = 1 - (1/r^(ฮณ-1)), where r is the compression ratio and ฮณ is the heat capacity ratio (Cp/Cv).
Outlines
๐ง Introduction to Thermodynamics and Heat Engines
This paragraph introduces the topic of thermodynamics, focusing on the second law and its implications for heat engines, efficiency, and refrigerators. It explains the first law of thermodynamics as a conservation of energy principle, using a simple example of energy transfer and work done by a system. The second law is introduced with the concept of irreversible processes increasing disorder, exemplified by a ball falling to the ground. The paragraph sets the stage for further exploration into heat engines and their efficiency, using the concepts of reversible and irreversible processes.
๐ฅ Understanding Irreversible and Reversible Processes
The paragraph delves deeper into the concepts of reversible and irreversible processes, using the analogy of a ball rolling on a level surface to illustrate a reversible process. It explains that heat naturally flows from hot to cold, which is a spontaneous process, and that reversing this flow would require energy input, which is non-spontaneous. The second law of thermodynamics is further clarified as the tendency for heat to flow from hot to cold, with the example of equal temperatures reaching a state of equilibrium where heat flow in both directions is balanced.
๐ Mechanics of Heat Engines and Their Efficiency
This section introduces the concept of a heat engine, which converts heat energy into mechanical work. It describes the process of heat flow from a high-temperature to a low-temperature reservoir and how a fraction of this heat is converted into work, while the rest is expelled into the environment. The paragraph explains the formula for calculating work and efficiency in heat engines, providing an example where a heat engine absorbs 2500 joules and discards 2100 joules, resulting in a work output and efficiency calculation.
๐ก๏ธ Calculating Work and Efficiency in Heat Engines
The paragraph continues the discussion on heat engines, providing a step-by-step calculation of work performed and thermal efficiency for different scenarios. It explains how to determine the amount of heat absorbed by an engine per cycle and how to calculate the work output over multiple cycles. The paragraph also addresses the concept of power, differentiating it from work and explaining its unit as the watt. Several examples are given, including a diesel engine and a gasoline engine, to illustrate the calculations.
๐ The Carnot Cycle and Its Ideal Efficiency
This section introduces the Carnot cycle, an ideal model of a heat engine that represents the maximum possible efficiency. The paragraph explains the steps of the Carnot cycle using a PV diagram, including isothermal expansion and compression, and adiabatic expansion and compression. It also presents the formulas for calculating the efficiency of a Carnot engine and the relationship between the heat energy absorbed and released by the engine, using an example to demonstrate the calculations.
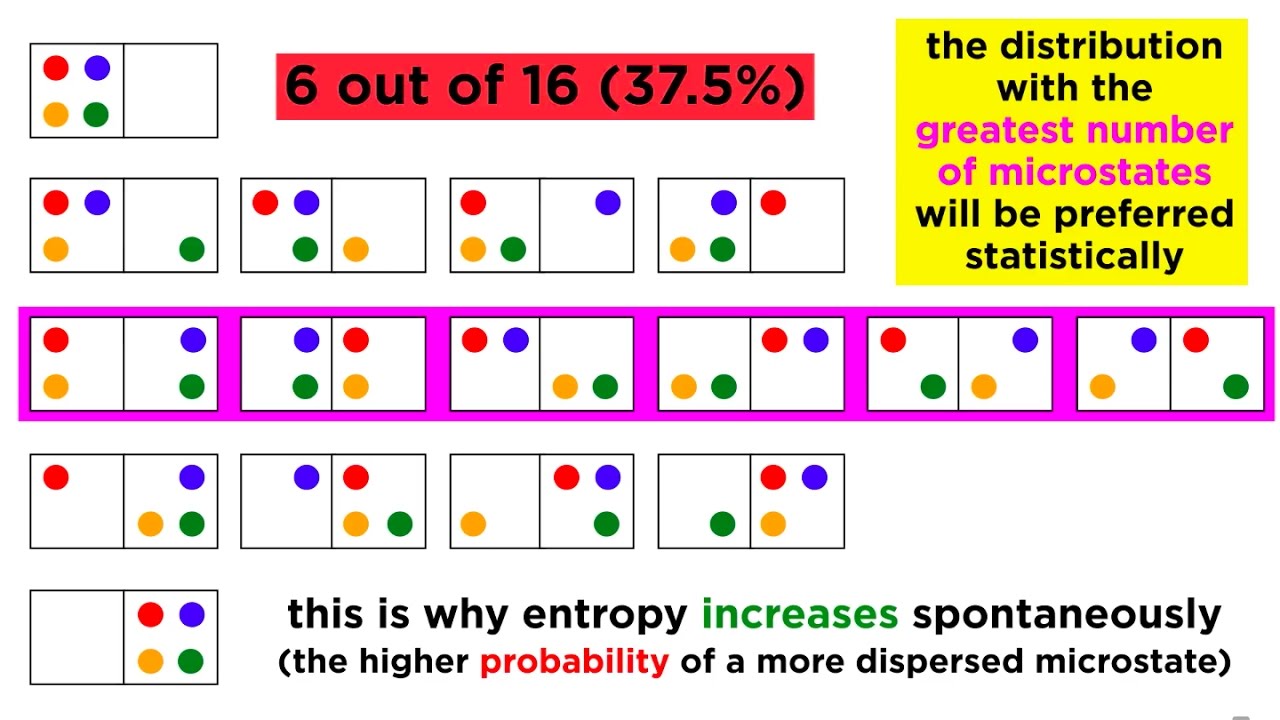
๐๏ธ Entropy and the Second Law of Thermodynamics
The paragraph discusses entropy as a measure of disorder in a system, explaining how it tends to increase for irreversible processes and can remain constant for reversible processes in an isolated system. It uses the analogy of a room becoming messy to illustrate the concept of increasing disorder. The paragraph also explains how entropy is related to heat transfer and temperature, and how it can be calculated using the formula ฮS = Q/T for reversible isothermal processes.
๐ The Working of Refrigerators and Air Conditioners
This section contrasts the operation of refrigerators and air conditioners with that of heat engines. It explains that these devices use electricity to pump heat from a cold to a hot reservoir, opposite to the natural flow of heat. The paragraph introduces the concept of the coefficient of performance (COP) as a measure of efficiency for refrigerators and heat pumps, and it differentiates between the COP for refrigerators, which is concerned with heat removed from the cold reservoir, and that for heat pumps, which is concerned with heat delivered to the warm environment.
โ๏ธ Calculating Performance of Refrigerators and Heat Pumps
The paragraph provides a detailed explanation of how to calculate the coefficient of performance for refrigerators and heat pumps, using the Carnot efficiency as the maximum ideal performance. It walks through examples of calculating the COP for a refrigerator using a given amount of work and heat transferred, and for a Carnot freezer, using the temperatures of the hot and cold reservoirs. The section also explains how to find the heat energy transferred to the hot reservoir for a Carnot device.
๐ง The Otto Cycle and Its Efficiency
This section introduces the Otto cycle, an ideal model for gasoline engines, and explains its steps using a PV diagram. The paragraph details the processes of adiabatic compression, isochoric heating, adiabatic expansion, and isochoric cooling that make up the cycle. It also presents the formula for calculating the efficiency of an Otto cycle in terms of the compression ratio and the gamma ratio, providing examples to illustrate the calculations.
๐ Entropy Calculation in Phase Changes and Temperature Variations
The paragraph discusses the calculation of entropy changes during phase changes and temperature variations. It explains that the change in entropy during the melting of ice can be calculated using the formula ฮS = Q/T, with Q being the heat transferred. The section also addresses how to estimate and calculate entropy changes when the temperature is not constant, using both an average temperature method and an integral calculus method, providing examples for each.
๐ก๏ธ Entropy Changes in Adiabatic Processes and Mixing of Water
This section explains that for adiabatic processes, the change in entropy is zero because there is no exchange of heat with the surroundings. It also discusses the entropy change when mixing water at different temperatures, using both the average temperature method and the natural log function to calculate the total change in entropy. The paragraph emphasizes the importance of using the correct temperatures in kelvin for these calculations.
Mindmap
Keywords
๐กThermodynamics
๐กFirst Law of Thermodynamics
๐กSecond Law of Thermodynamics
๐กHeat Engines
๐กEfficiency
๐กEntropy
๐กReversible and Irreversible Processes
๐กCarnot Engine
๐กRefrigerators and Air Conditioners
๐กCoefficient of Performance (COP)
๐กAuto Cycle
Highlights
Introduction to the second law of thermodynamics and its focus on solving problems related to heat engines, efficiency, the Carnot engine, and refrigerators.
Explanation of the first law of thermodynamics as a statement of conservation of energy, demonstrated through the change in internal energy equation.
Illustration of the concept of reversible and irreversible processes using the example of a ball falling and rolling on a level surface.
Clarification of the second law of thermodynamics, emphasizing the natural flow of heat from hot to cold and the increase in disorder in irreversible processes.
Discussion on the establishment of equilibrium when temperatures are approximately equal, leading to a reversible process with no net heat flow.
Introduction to heat engines as devices converting heat energy into mechanical work, with an explanation of the process using a temperature reservoir example.
Calculation of work performed by a heat engine and its thermal efficiency, using the formula work = qh - qc and efficiency = (work / qh) * 100%.
Problem-solving approach for a heat engine that absorbs and discards heat, demonstrating the calculation of work output and thermal efficiency.
Explanation of the concept of power in the context of heat engines, relating power to work done over time and the unit conversion to watts.
Use of the Carnot cycle as an ideal model for heat engines to represent maximum possible efficiency, with a description of its PV diagram.
Introduction to the coefficient of performance for refrigerators and air conditioners, contrasting it with the efficiency of heat engines.
Calculation of the coefficient of performance for a refrigerator, using the formula k = qc / w, and comparison with the Carnot coefficient.
Explanation of the Otto cycle, an ideal model for gasoline engines, detailing its PV diagram and the process of adiabatic compression and isochoric heating.
Calculation of entropy change in a system, using the formula ฮS = q / T, and its application in isothermal processes.
Estimation and exact calculation of entropy change during a temperature change, using average temperature and natural log functions.
Discussion on the entropy change during an adiabatic process, highlighting that it is zero for a complete cycle in an ideal system.
Calculation of total change in entropy when mixing water at different temperatures, using both estimation and exact calculation methods.
Conclusion summarizing the key points of thermodynamics covered in the video, including the laws, efficiency calculations, and entropy changes.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: