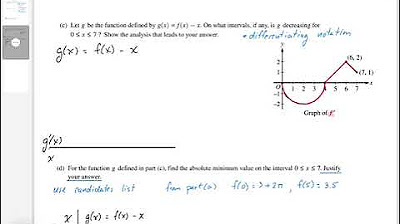AP Precalculus Practice Exam Question 21
TLDRThe video script discusses a rational function f(x) graphed in the XY plane, with a numerator polynomial having a zero at x=1 but not at x=7. The denominator polynomial has zeros at both x=1 and x=7, with equal multiplicities. The script explores the implications on the graph of f(x), concluding that there is a hole at x=1 and a vertical asymptote at x=7. The correct statement among the options provided is that the graph of f has a hole at x=1 and a vertical asymptote at x=7, which is identified as choice C.
Takeaways
- 📚 The function f(x) is a rational function composed of a polynomial in the numerator and a polynomial in the denominator.
- 🔍 The numerator of f(x) has a zero at x=1, indicating the presence of a factor (x-1).
- 🚫 The numerator does not have a zero at x=7, meaning there is no factor (x-7).
- 📐 The denominator of f(x) has zeros at both x=1 and x=7, including factors (x-1) and (x-7).
- 🔄 The multiplicities of the zeros at x=1 in both the numerator and denominator are equal, simplifying to a common exponent for the factors.
- 🌀 For simplicity, the script assumes the multiplicities are both set to 3, but they could be any equal power.
- ❌ Option A is incorrect because there is a hole at x=1 but not at x=7, which is a vertical asymptote.
- 🔄 Option B is incorrect as it reverses the characteristics of the graph at x=1 and x=7.
- ✅ Option C is correct, stating that there is a hole at x=1 and a vertical asymptote at x=7.
- ❌ Option D is incorrect because it incorrectly identifies both x=1 and x=7 as vertical asymptotes.
- 📝 The correct answer to the question is C, which accurately describes the graph of f(x).
Q & A
What is a rational function in the context of the script?
-A rational function is a mathematical function that is expressed as the ratio of two polynomials, with both a numerator and a denominator.
Why does the polynomial in the numerator have a zero at x equals one?
-The polynomial in the numerator has a zero at x equals one because it contains a factor of (x - 1), which when x is one, results in zero.
Why does the polynomial in the numerator not have a zero at x equals seven?
-The polynomial in the numerator does not have a zero at x equals seven because it does not contain a factor of (x - 7).
What does it mean for the polynomial in the denominator to have a zero at both x equals one and x equals seven?
-The polynomial in the denominator having zeros at both x equals one and x equals seven means it contains factors of (x - 1) and (x - 7), indicating that the function will approach infinity at these points unless the numerator also has these factors.
What is the significance of the multiplicities of the zeros in the numerator and the denominator being equal?
-The equal multiplicities of the zeros in the numerator and the denominator ensure that the function does not have a vertical asymptote at x equals one, as the factors cancel out, resulting in a hole in the graph instead.
Why is there a vertical asymptote at x equals seven in the graph of f(x)?
-There is a vertical asymptote at x equals seven because the denominator has a zero at x equals seven, but the numerator does not have a corresponding zero to cancel it out, causing the function to approach infinity.
What is the difference between a hole and a vertical asymptote in the graph of a rational function?
-A hole in the graph occurs when the zeros in the numerator and denominator have the same multiplicity, causing them to cancel out and not affect the behavior of the function at that point. A vertical asymptote occurs when the denominator has a zero that is not canceled out by the numerator, causing the function to approach infinity.
What does the script suggest about the multiplicity of the factors (x - 1) and (x - 7) in the denominator?
-The script suggests that for simplicity, the multiplicity of the factors (x - 1) and (x - 7) in the denominator is assumed to be three, but it could be any equal power that does not affect the conclusion about the behavior of the function.
Why is the statement 'the graph of f has a hole at both x equals one and x equals seven' incorrect according to the script?
-This statement is incorrect because while there is a hole at x equals one due to the cancellation of the (x - 1) factor in both the numerator and the denominator, there is a vertical asymptote at x equals seven due to the lack of a corresponding factor in the numerator to cancel out the zero in the denominator.
Which of the provided options correctly describes the behavior of the graph of f(x) according to the script?
-Option C is correct, stating that the graph of f has a hole at x equals one and a vertical asymptote at x equals seven.
Why is the statement 'the graph of f has a vertical asymptote at both one and seven' incorrect?
-This statement is incorrect because, as per the script, there is a hole at x equals one due to the cancellation of factors, while there is a vertical asymptote at x equals seven due to the uncancelled zero in the denominator.
Outlines
📈 Analysis of a Rational Function's Graph
The paragraph discusses a rational function, f(x), graphed on the XY plane. It specifies that the numerator of f(x) has a zero at x=1 due to the factor (x-1), but not at x=7. The denominator has zeros at both x=1 and x=7, indicated by the factors (x-1) and (x-7), with equal multiplicities, simplified in the explanation to a cubic power for ease. The paragraph then reviews multiple-choice questions about the function's graph, concluding that the graph has a hole at x=1 and a vertical asymptote at x=7, leading to the correct answer being option C.
Mindmap
Keywords
💡Rational Function
💡Graph
💡Zero
💡Numerator
💡Denominator
💡Multiplicity
💡Vertical Asymptote
💡Hole
💡Factor
💡Polynomial
💡Exponent
Highlights
The function f(x) is a rational function composed of two polynomials in the numerator and denominator.
The numerator of f(x) has a zero at x=1, indicating a factor of (x-1).
The numerator does not have a zero at x=7, meaning it lacks a factor of (x-7).
The denominator of f(x) has zeros at both x=1 and x=7, with factors of (x-1) and (x-7).
The multiplicities of the zeros at x=1 in both the numerator and denominator are equal.
For simplicity, the multiplicities are assumed to be cubic, but they could be any equal power.
Option A suggests a hole at both x=1 and x=7, which is incorrect due to the vertical asymptote at x=7.
Option B incorrectly states a vertical asymptote at x=1 and a hole at x=7.
Option C correctly states a hole at x=1 and a vertical asymptote at x=7.
Option D incorrectly suggests vertical asymptotes at both x=1 and x=7.
The correct answer is C, which accurately describes the graph of f(x).
A vertical asymptote occurs where the denominator has a zero not canceled by the numerator.
A hole in the graph is formed when the zero in the denominator is canceled by an equal zero in the numerator.
The degrees of the factors in the numerator and denominator must match for a hole to form.
The concept of multiplicity is crucial for determining the nature of the graph's behavior at zeros.
Understanding the difference between holes and vertical asymptotes is key to analyzing rational functions.
The function's behavior at x=1 and x=7 is determined by the interaction of factors in the numerator and denominator.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: